Kiểm tra ngẫu nhiên 200 người lái xe mô-tô thấy 12 người không có bằng lái. Biết số người có xe mô tô là 10000. Hãy tìm khoảng tin cậy 98% đối với số người lái xe không có bằng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

A B C H D E K I
a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)

Olm chào em, cảm ơn em đã đồng hành cùng olm. Khi làm bài luyện trên olm thì em cần chú ý đọc kỹ đề, đề yêu cầu gì thì trả lời cái đó. Nắm vững kiến thức cơ bản để vận dụng làm bài tập thì em sẽ chọn đúng đáp án của bài toán.
Chúc em học tập hiệu quả cùng olm, thân mến!

Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip

Gọi số đó là \(\overline{xyz}\). Theo đề bài, ta có \(2\left(yz+5\right)=x^2\) \(\Rightarrow x⋮2\)
Mà \(2\left(yz+5\right)\ge10\) nên \(x^2\ge10\Leftrightarrow x\ge4\)
\(\Rightarrow x\in\left\{4,6,8\right\}\)
Nếu \(x=4\) thì \(yz+5=8\Leftrightarrow yz=3\) \(\Rightarrow\left(y,z\right)\in\left\{\left(1;3\right),\left(3;1\right)\right\}\)
Nếu \(x=6\) thì \(yz+5=18\Leftrightarrow yz=13\), vô lí.
Nếu \(x=8\) thì \(yz+5=32\Leftrightarrow yz=27\) \(\Leftrightarrow yz\in\left\{\left(3;9\right),\left(9;3\right)\right\}\)
Vậy có 4 số thỏa mãn ycbt là 413, 431, 839, 893.

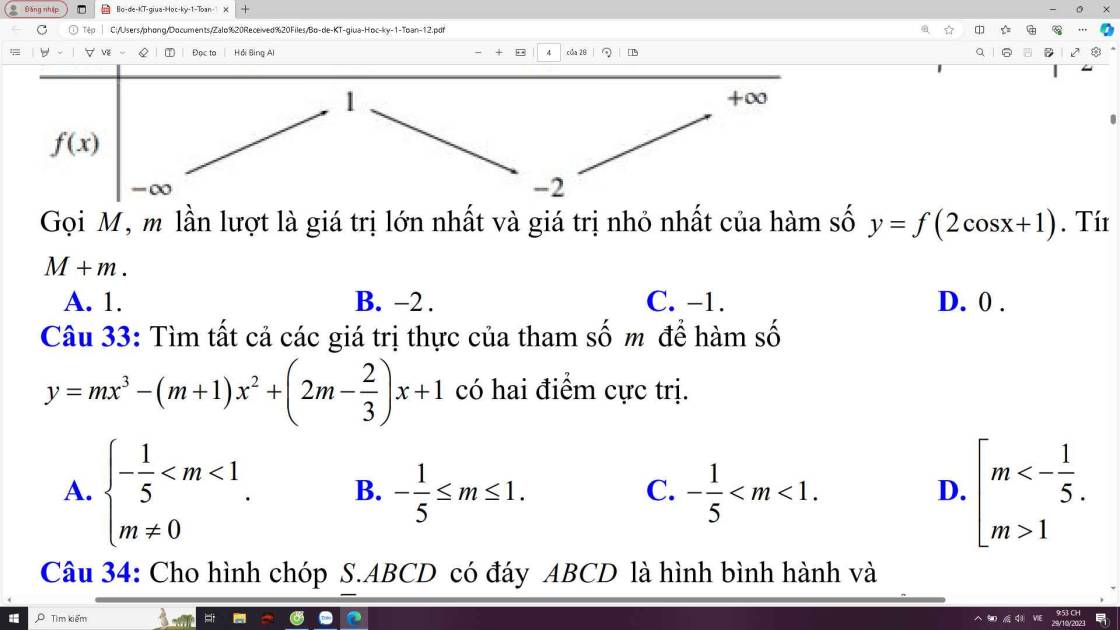
Từ bảng biến thiên bạn có thể vẽ được đồ thị hàm số $f(x)$
Khi đó pt : $f(x)=\frac{2019}{2}$ có nghiệm duy nhất $x\in (3;+\infty)$
Đáp án D.

Lời giải:
Để $y$ có 2 điểm cực trị thì:
$y'=3mx^2-2(m+1)x+2m-\frac{2}{3}=0$ có 2 nghiệm phân biệt.
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-3m(2m-\frac{2}{3})>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ -5m^2+4m+1>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ (1-m)(5m+1)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \frac{-1}{5}< m< 1\end{matrix}\right.\)
Đáp án A.