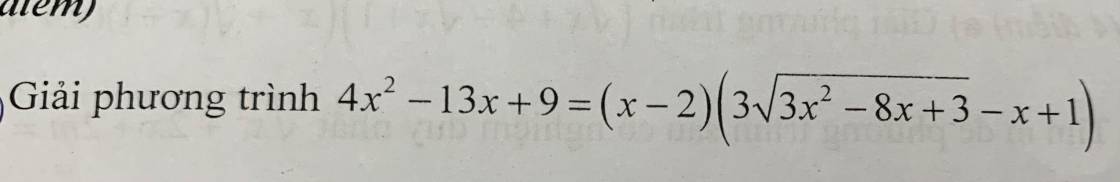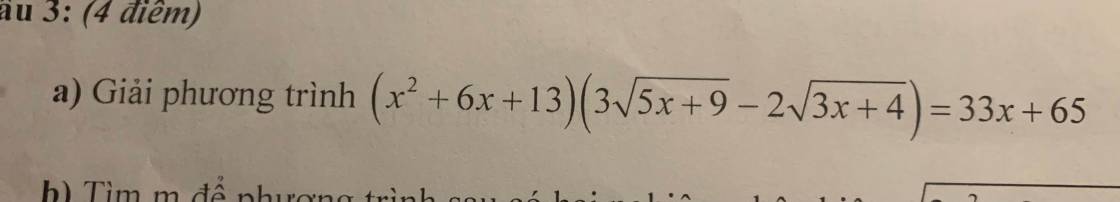làm ơn giải giúp mình với ,help me 10' thôi đó
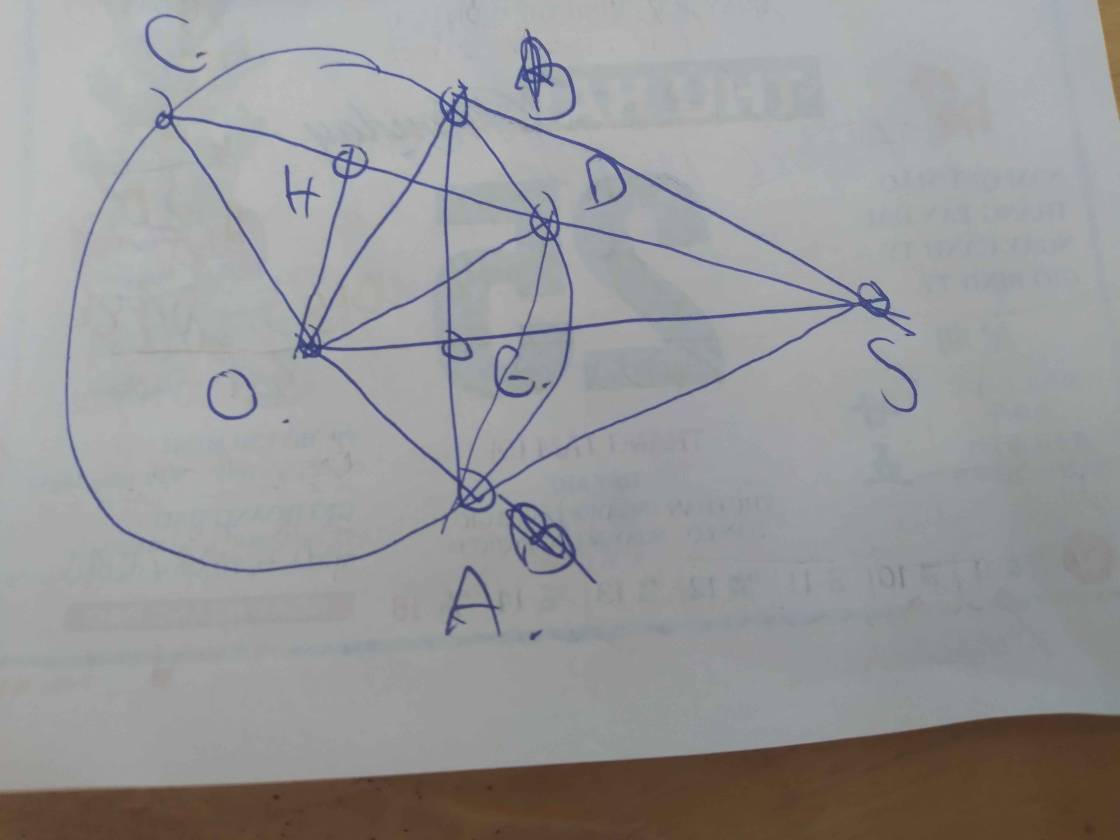
cho đường tròn (O,R) và dây cung CD cố định.Gọi H là trung điểm CD.Gọi S là 1 điểm bất kì trên tia đối của DC.Qua S kẻ 2 tiếp tuyến SA,SB tới đường tròn (O)(B thuộc cung CD nhỏ).Gọi E là giao điểm của AB và SO.
a)c/m SAOH nội tiếp 1 đường tròn
b)c/m SE*SO=SA2=SD*SC
c)c/m BE là phân giác của góc DEC