
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




3 - 4x(25 - 2x) = 8x² + x - 300
3 - 100x + 8x² = 8x² + x - 300
-100x + 8x² - 8x² - x = -300 - 3
-101x = -303
x = -303 : (-101)
x = 3
Vậy S = {3}

ĐKXĐ: \(x\notin\left\{0;3;-3;-\dfrac{3}{2}\right\}\)
\(\dfrac{x^2-6}{x-3}+\dfrac{x^2+3x}{2x+3}\left(\dfrac{x}{x^2-9}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\left(\dfrac{x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\dfrac{x^2-\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x^2-x^2-6x-9}{\left(2x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-6}{x-3}-\dfrac{3}{x-3}=\dfrac{x^2-9}{x-3}=x+3\)

Gọi vận tốc thật của thuyền là x(km/h)
(ĐK: x>10)
Vận tốc lúc đi là x+10(km/h)
Vận tốc lúc về là x-10(km/h)
Độ dài quãng đường lúc đi và lúc về là bằng nhau nên ta có:
4(x+10)=5(x-10)
=>5x-50=4x+40
=>x=90(nhận)
Vậy: Khoảng cách từ A đến B là \(4\left(90+10\right)=400\left(km\right)\)




a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: XétΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HB\cdot HC=HA^2\)
c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>\(\widehat{MAC}=\widehat{ACB}\)
\(\widehat{MAC}+\widehat{AED}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>DE\(\perp\)AM
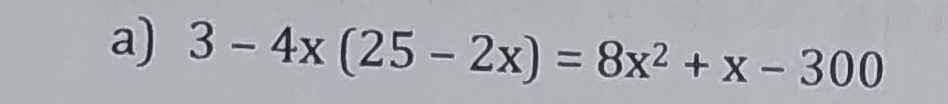
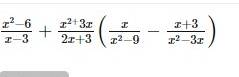 giúp tui zới mn oi bí quá
giúp tui zới mn oi bí quá
a: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
\(\widehat{DBA}\) chung
Do đó: ΔDBA~ΔABC
b: ΔDBA~ΔABC
=>\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\left(1\right)\)
Xét ΔBAD có BF là phân giác
nên \(\dfrac{BD}{BA}=\dfrac{FD}{FA}\left(2\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AE}{EC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{FD}{FA}=\dfrac{AE}{EC}\)
=>\(FD\cdot EC=AE\cdot FA\)