Tìm giá trị nhỏ nhất của biểu thức A = \(\dfrac{\left|x-2022\right|+2023}{\left|x-2022\right|+2024}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔAMB=ΔAMC
=>MB=MC
=>M là trung điểm của BC
c: ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
mà IH\(\perp\)BC
nên AM//IH
=>\(\widehat{BIH}=\widehat{BAM}\)
mà \(\widehat{BAC}=2\cdot\widehat{BAM}\)(AM là phân giác của góc BAC)
nên \(\widehat{BAC}=2\cdot\widehat{BIH}\)
a) Do AB = AC và AM là tia phân giác của góc A nên tam giác AMB cân tại A và tam giác AMC cân tại A.
- Ta có góc BAM = góc CAM (do AM là tia phân giác).
=> Vậy tam giác AMB = tam giác AMC (các cạnh tương ứng bằng nhau).
b) Do tam giác AMB = tam giác AMC nên BM = MC.
=> Vậy M là trung điểm của BC.
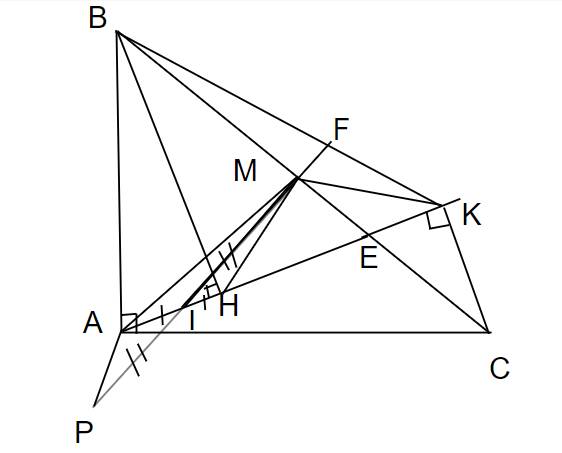
c) Do ∠BAI = ∠CAK (do AK là tia phân giác của ∠BAC) và ∠BAI = ∠BHI (do IH ⊥ BC và AI // BC) nên ∠CAK = ∠BHI.
- Lại có ∠ACK = ∠BHK (do CK = KH và AC // BH).
=> Vậy tam giác ACK = tam giác BHK (các góc tương ứng bằng nhau) nên ∠BAC = 2∠BIH (do ∠BAC = ∠ACK + ∠CAK = ∠BHK + ∠BHI = 2∠BIH).
~~~~~~
+) ∠ là góc nhé ^^

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
=>DB=DC
c:
Ta có: DB và DE là hai tia đối nhau
=>D nằm giữa B và E
mà DB=DE
nên D là trung điểm của BE
Xét ΔCEB có
CD là đường trung tuyến
\(CG=\dfrac{2}{3}CD\)
Do đó: G là trọng tâm của ΔCEB
Xét ΔCEB có
G là trọng tâm
M là trung điểm của BC
Do đó; E,G,M thẳng hàng


Gọi số công nhân trong đội lúc đầu là $x$.
Theo đề bài, ta có:
$x \cdot 30 = (x + 10) \cdot 20$
Giải trên, ta được: $x = 20$
Vậy, số công nhân trong đội lúc đầu là 20 người.

Gọi giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là a(đồng),b(đồng),c(đồng)
Vì số tiền để cô Mai mua táo bằng số tiền mua bưởi và dưa hấu nên 3a=6b=10c
=>\(\dfrac{3a}{30}=\dfrac{6b}{30}=\dfrac{10c}{30}\)
=>\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}\)
Giá 1kg bưởi hơn 1kg dưa hấu 18000 đồng nên b-c=18000
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}=\dfrac{b-c}{5-3}=\dfrac{18000}{2}=9000\)
=>\(a=9000\cdot10=90000;b=9000\cdot5=45000;c=9000\cdot3=27000\)
Vậy: giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là 90000 đồng; 45000 đồng; 27000 đồng

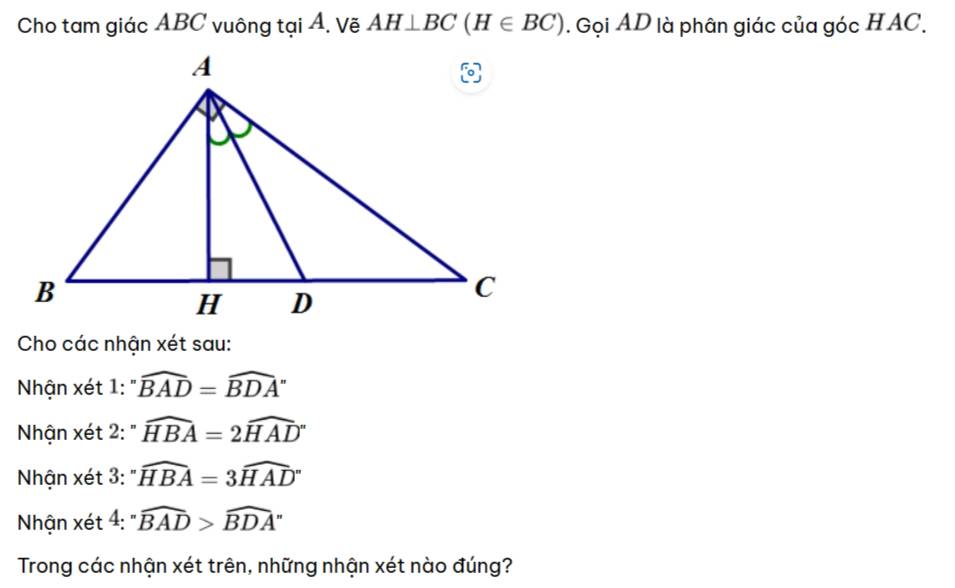
a: Sửa đề: ΔBAD=ΔBED
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Xét ΔMDH và ΔMCB có
\(\widehat{MDH}=\widehat{MCB}\)(hai góc so le trong, DH//BC)
MD=MC
\(\widehat{DMH}=\widehat{CMB}\)(hai góc đối đỉnh)
Do đó: ΔMDH=ΔMCB
=>DH=CB

a)Ta có tam giác ABC cân
=>:AB=AC;góc B=góc C.
Xét tam giác AMB và tam giác AMC có:
AB=AC(cmt)
góc BAM=góc CAM (AM là phân giác của góc A).
AM chung.
=>tam giác AMB = tam giác AMC(c-g-c)
b) Vì tam giác AMB = tam giác AMC
=>góc AMB=góc AMC (2 góc tương ứng)
Mà 2 góc ở vị trí kề bù => góc AMB=góc AMC=180:2=90độ
=>AM vuông góc BC
c)

\(A=\dfrac{\left|x-2022\right|+2024-1}{\left|x-2022\right|+2024}=1-\dfrac{1}{\left|x-2022\right|+2024}\)
Do \(\left|x-2022\right|\ge0;\forall x\Rightarrow\left|x-2022\right|+2024\ge2024\)
\(\Rightarrow-\dfrac{1}{\left|x-2022\right|+2024}\ge-\dfrac{1}{2024}\)
\(\Rightarrow A\ge1-\dfrac{1}{2024}=\dfrac{2023}{2024}\)
\(A_{min}=\dfrac{2023}{2024}\) khi \(x-2022=0\Rightarrow x=2022\)