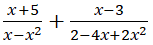x2+6x-m là bình phương của 1 tổng thì giá trị m là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chúng ta được sinh ra và nuôi dưỡng trong vòng tay yêu thương của gia đình. Và trường học sẽ là mảnh đất tốt tươi để ươm mầm tri thức cho mỗi người, là bước đệm để mỗi chúng ta vươn tới tương lai rực rỡ. Ở nơi đó, chúng ta được thầy cô – người mẹ hiền thứ hai, sẽ dạy dỗ, truyền tải những tri thức khoa học, là hành trang quan trọng theo chúng ta suốt cả cuộc đời. Thầy cô còn dạy ta biết yêu thương, biết ứng xử sao cho đúng đắn với mọi người. Không những vậy, trường học là một thế giới thu nhỏ nơi có bạn bè, để cùng sẻ chia niềm vui nỗi buồn, cùng nhau đoàn kết để tạo nên sức mạnh trong mỗi tập thể lớp. Ngôi trường là nơi nuôi dưỡng và chắp cánh cho những ước mơ, hoài bão của những cô cậu học trò. Ở thế giới đó, chúng ta được yêu thương và che chở, được học làm người trước khi bước ra cánh cửa cuộc đời rộng lớn và khắc nghiệt hơn. Có thể nói, mái trường như ngôi nhà lớn thứ hai, che chở cho ta trong suốt những năm tháng học trò tươi đẹp.
Trong đời sống xã hội, giáo dục và đào tạo là lĩnh vực có vai trò quan trọng đối với mọi quốc gia, dân tộc ở mọi thời đại. Trong xu thế phát triển tri thức ngày nay, giáo dục - đào tạo được xem là chính sách, biện pháp quan trọng hàng đầu để phát triển ở nhiều quốc gia trên thế giới và Việt Nam không phải là ngoại lệ. Giáo dục góp phần nâng cao dân trí ở mọi quốc gia, dân tộc. Ngày nay, giáo dục và đào tạo còn góp phần tạo ra hệ thống giá trị xã hội mới. Trong nền kinh tế tri thức hiện nay, tri thức là sản phẩm của giáo dục và đào tạo, đồng thời là tài sản quý giá nhất của con người và xã hội. Sở hữu tri thức trở thành sở hữu quan trọng nhất được các nước thừa nhận và bảo hộ. Nguồn lực phát triển kinh tế - xã hội ở mỗi quốc gia, dân tộc từ tài nguyên, sức lao động cơ bắp là chính chuyển sang nguồn lực con người có tri thức là cơ bản nhất. Giáo dục và đào tạo góp phần bảo vệ chế độ chính trị của mỗi quốc gia, dân tộc bởi giáo dục - đào tạo góp phần xây dựng đội ngũ lao động có trình độ cao làm giàu của cải vật chất cho xã hội đồng thời có bản lĩnh chính trị vững vàng, đủ sức đề kháng chống lại các cuộc “xâm lăng văn hóa” trong chính quá trình hội nhập quốc tế và toàn cầu. Nhận thức rõ vai trò của giáo dục - đào tạo đối với sự phát triển, Đảng và Nhà nước ta khẳng đinh: “Giáo dục là quốc sách hàng đầu”. Việc đổi mới giáo dục trong giai đoạn hiện nay đang là mối quan tâm của các cấp, ngành, các nhà khoa học và toàn xã hội. Chọn khoa học và giáo dục làm khâu đột phá cho phát triển. Chọn giáo dục làm tiền đề, làm xương sống của phát triển bền vững là xác định đúng đắn và khoa học.
Giáo dục luôn là quốc sách hàng đầu mà Đảng và nhà nước ta đề ra trong những nhiệm vụ để xây dựng đất nước. Và nhà trường có vai trò vô cùng to lớn trong sự nghiệp phát triển giáo dục. Nhà trường góp phần giáo dục lên thế hệ trẻ, những chủ nhân tương lai của đất nước. Trước hết phải nói rằng, nhà trường chính là cái nôi ươm mầm của thế hệ trẻ. Là nơi dạy dỗ, truyền tải những tri thức về mọi mặt trong cuộc sống cho chúng ta. Từ những kiến thức căn bản trong cuộc sống, những văn hóa ứng xử hàng ngày. Từ đạo đức cho tới kiến thức. Tất cả mọi thứ đều có thể học tập được ở nhà trường. Mà người truyền tải cho chúng ta những tri thức ấy, là những người thầy cô. Vẫn miệt mài ngày đêm dạy dỗ lớp lớp học trò. Để chắp cánh ước mơ cho biết bao nhiêu thế hệ trẻ bay cao. Nhà trường còn là một nơi kì diệu. Đây là một thế giới của những điều mới lạ mà chúng ta tiếp xúc trước tiên, trước khi ra ngoài xã hội bươn trải. Là thế giới của tình bạn, tình thầy trò, tình yêu thương. Trong nhà trường, mỗi lớp học là một tập thể. Và mỗi tập thể luôn có sự gắn bó, đoàn kết với nhau. Nhà trường dạy cho chúng ta cách đoàn kết làm một. Cùng nhau vượt qua khó khăn trong học tập để vươn lên. Là cùng nhau sẻ chia những nỗi buồn, niềm vui mà bạn bè mình gặp phải. Là nơi của những tấm lòng nhân hậu, sẵn sàng giúp đỡ bạn bè của mình khi có người gặp khó khăn. Là nơi chắp cánh cho những ước mơ của những thế hệ trẻ.

Answer:
\(x-x^2=x\left(1-x\right)\)
\(2-4x+2x^2=2\left(1-2x+x^2\right)=2\left(1^2-2.1.x+x^2\right)=2\left(1-x^2\right)\)
Phận hệ số của hai mẫu thức lần lượt là 1 và 2.
=> BCNN(1; 2) = 2
=> Ta chọn phần hệ số cho mẫu chung là 2
Phần biến lần lượt là \((1-x)\) và \((1-x)^2\)
=> Số mũ lớn nhất là \((1-x)^2\)
=> Ta chọn phần biến cho mẫu thức chung là \((1-x)^2\)
=> Mẫu thức chung của hai phân thức trên là \(2\left(1-x\right)^2\)


Bạn cần nhớ công thức tính thể tích là V = chiều dài x chiều rộng x chiều cao, bạn chỉ cần nhân cả 3 cạnh với nhau là ra thể tích .