Cho tam giác ABC vuông tại A có AB=3cm ; AC=4cm . Vẽ phân giác BD ( D thuộc AC ) , từ D vẽ DE vuông góc với BC ( E thuộc BC )
a) Chứng minh tam giác ABD = tam giác EBD
b) Gọi giao điểm của DE và BA là F .Chứng minh DF > DE
Giúp mik vs , đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Áp dụng TCDTSBN:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}=\frac{a(bz-cy)}{a^2}=\frac{b(cx-az)}{b^2}=\frac{c(ay-bx)}{c^2}$
$=\frac{a(bz-cy)+b(cx-az)+c(ay-bx)}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\RIghtarrow bz=cy, cx=az$
$\Rightarrow \frac{x}{a}=\frac{z}{c}; \frac{z}{c}=\frac{y}{b}$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$
Ta có đpcm.

Giải:
Một công nhân sẽ hoàn thành công việc đó trong:
180 x 50 = 9 000 (ngày)
Thực tế số công nhân làm việc đó là:
50 - 5 = 45 (công nhân)
Vậy với 45 công nhân thì sẽ hoàn thành công việc đó trong:
9 000 : 45 = 200 (ngày)
Kết luận:..

B = 2\(x^2\) + y; \(x=1\); y = 1
Thay \(x=1\); y = 1 vào B ta có:
B = 2.12 + 1
B = 2 + 1
B = 3
Thay x=1 và y=1 vào B, ta được:
\(B=2\cdot1^2+1=2+1=3\)

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
b: Ta có: ΔBAD=ΔBMD
=>DA=DM
mà DM<DC
nên DA<DC
c: Xét ΔBKC có
KM,CA là các đường cao
KM cắt CA tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC tại N
Xét ΔKBC có
BN là đường cao
BN là đường phân giác
Do đó: ΔKBC cân tại B

a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
NP chung
\(\widehat{KNP}=\widehat{HPN}\)(ΔMPN cân tại M)
Do đó: ΔKNP=ΔHPN
b: Ta có: ΔKNP=ΔHPN
=>\(\widehat{KPN}=\widehat{HNP}\)
=>\(\widehat{ENP}=\widehat{EPN}\)
=>ΔENP cân tại E
c: Xét ΔMEN và ΔMEP có
ME chung
EN=EP
MN=MP
Do đó: ΔMEN=ΔMEP
=>\(\widehat{EMN}=\widehat{EMP}\)
=>ME là phân giác của góc NMP

Lời giải:
a.
Ta thấy: $AB< AC< BC$
$\Rightarrow \widehat{C}< \widehat{B}< \widehat{A}$ (tính chất góc đối diện cạnh lớn hơn thì lớn hơn)
b.
Xét tam giác $BDC$ có $CA, DK$ là 2 đường trung tuyến cắt nhau tại $M$ nên $M$ là trọng tâm tam giác $BDC$
$\Rightarrow MC=\frac{2}{3}CA=\frac{2}{3}.8=\frac{16}{3}$ (cm)
c.
Do $Q$ nằm trên đường trung trực của $AC$ nên $QC=QA(1)$
$\Rightarrow QAC$ là hình tam giác cân tại $Q$
$\Rightarrow \widehat{QAC}=\widehat{QCA}$
$\Rightarrow 90^0-\widehat{QAC}=90^0-\widehat{QCA}$
$\Rightarrow \widehat{DAQ}=\widehat{QDA}$
$\Rightarrow QAD$ cân tại $Q$
$\Rightarrow QA=QD(2)$
Từ $(1); (2)\Rightarrow QD=QC$
$\Rightarrow BQ$ là trung tuyến của tam giác $BDC$ ứng với cạnh $DC$
Mà theo phần b, $M$ là trọng tâm của $BDC$ nên $BM$ cũng là đường trung tuyến của $BDC$ ứng với cạnh $DC$
$\Rightarrow B,Q,M$ thẳng hàng.
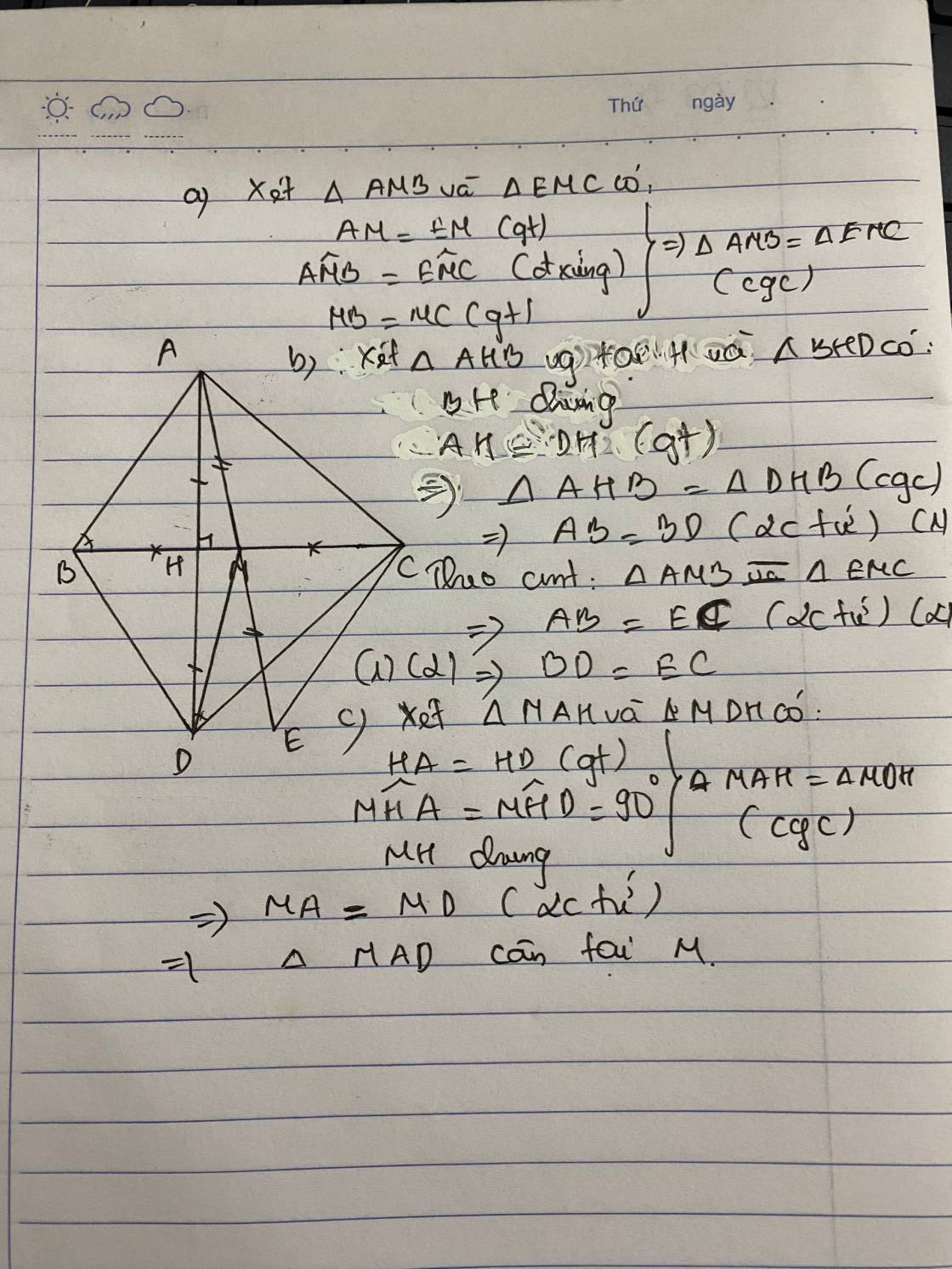







a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>DA=DE
mà DA<DF(ΔDAF vuông tại A)
nên DE<DF
=>DF>DE