cho 0<hoặc x,y,z< hoặc = 2 thm x+y+z=3.tìm gtln của x^3+y^3+z^3-3xyz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


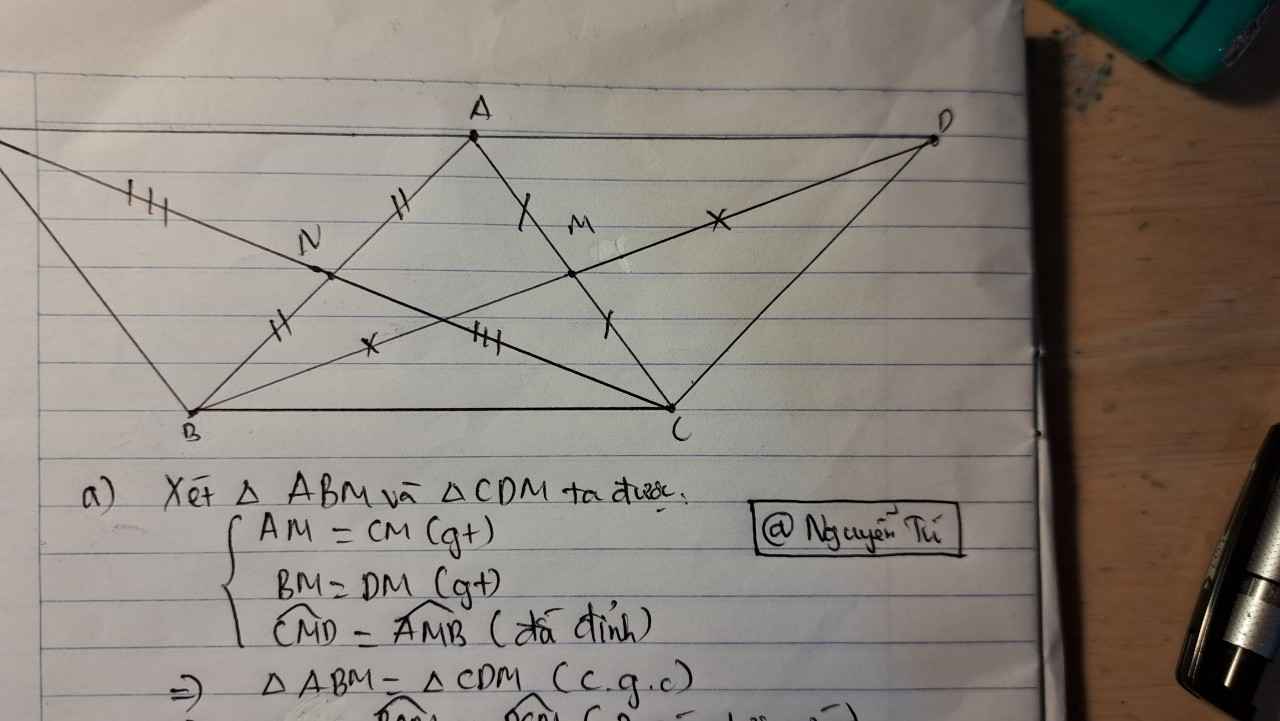
a: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
ΔMAB=ΔMCD
=>AB=CD
b: Xét ΔNBC và ΔNAE có
NB=NA
\(\widehat{BNC}=\widehat{ANE}\)(hai góc đối đỉnh)
NC=NE
Do đó: ΔNBC=ΔNAE
=>\(\widehat{NBC}=\widehat{NAE}\)
=>BC//AE
ΔNBC=ΔNAE
=>BC=AE
Xét ΔMBC và ΔMDA có
MB=MD
\(\widehat{BMC}=\widehat{DMA}\)(hai góc đối đỉnh)
MC=MA
Do đó: ΔMBC=ΔMDA
=>\(\widehat{MBC}=\widehat{MDA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BC//DA
ΔMBC=ΔMDA
=>BC=DA
Ta có: BC//DA
BC//AE
mà AD,AE có điểm chung là A
nên D,A,E thẳng hàng
mà AD=AE(=BC)
nên A là trung điểm của DE

Có thể lập được 6 số là: 1350, 1530, 3150, 3510, 5130, 5310
Có thể lập được 6 số là: 1350, 1530, 3150, 3510, 5130, 5310
hok tốt

\(M=x^2-4x+8\\ =\left(x^2-4x+4\right)+4\\ =\left(x-2\right)^2+4\)
Ta có:
`(x-2)^2>=0` với mọi x
`=>M=(x-2)^2+4>=4` với mọi x
Dấu "=" xảy ra: `x-2=0<=>x=2`
Vậy: ...


TH1: \(-\dfrac{1}{2}\le x\le\dfrac{5}{3}\)
\(\left(2x+1\right)+\left(5-3x\right)=6\\ =>2x+1+5-3x=6\\ =>\left(2x-3x\right)+6=6\\ =>x=0\left(tm\right)\)
TH2: \(x>\dfrac{5}{3}\)
\(\left(2x+1\right)-\left(5-3x\right)=6\\ =>2x+1-5+3x=6\\ =>2x+3x=6-1+5\\ =>5x=10\\ =>x=\dfrac{10}{5}=2\left(tm\right)\)
TH3: \(x< -\dfrac{1}{2}\)
\(-\left(2x+1\right)+\left(5-3x\right)=6\\ =>-2x-1+5-3x=6\\ =>-2x-3x+4=6\\ =>-5x=6-4=2\\ =>x=-\dfrac{2}{5}\left(ktm\right)\)

Số số hạng là (99-1):2+1=98:2+1=50(số)
D=(99+1)x50:2=502=2500

A D B C E I G K
Xét tg ABD
BD=BA (gt) => tg ABD cân tại B \(\Rightarrow\widehat{BAD}=\widehat{BDA}\)
\(\widehat{B}=\widehat{BAD}+\widehat{BDA}=2\widehat{BDA}\) (Trong tg góc ngoài bằng tổng 2 góc trong không kề với nó
Xét tg ACE
CE=CA(gt) => tg ACE cân tại C \(\Rightarrow\widehat{CAE}=\widehat{CEA}\)
\(\widehat{C}=\widehat{CAE}+\widehat{CEA}=2\widehat{CEA}\)
Xét tg ABC
\(\widehat{B}>\widehat{C}\left(gt\right)\) \(\Rightarrow2\widehat{BDA}>2\widehat{CEA}\Rightarrow\widehat{BDA}>\widehat{CEA}\)
Xét tg ADE có
\(\widehat{BDA}>\widehat{CEA}\Rightarrow AE>AD\) (Trong tg cạnh dối diện góc lớn hơn thì có độ dài lớn hơn)
b/
Xét tg cân ABD có
\(AG=BG\left(gt\right)\Rightarrow BG\perp AB\) (Trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao) \(\Rightarrow IG\perp AB\)
=> tg AID cân tại I (Tam giác có đường cao đồng thời là đường trung tuyến là tg cân => IA=ID
C/m tương tự ta cùng có tg AIE cân tại I => IA=IE
=> ID=IE=IA => tg DIE cân tại I
Qua I dựng đường thẳng d vuông góc với DE => d thuộc đường cao của tg DIE => I thuộc trung trực của tg DIE (Trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường trung trực
\(\Rightarrow I\in d\) là đường trung trực của DE
c/
ID=IA=IE => tg ADE nội tiếp đường tròn (I)
\(\Rightarrow sđ\widehat{BDA}=\dfrac{1}{2}sđcungAE\) (góc nội tiếp)
Ta có
\(sđ\widehat{AIE}=sđcungAE\) (góc ở tâm)
\(\Rightarrow\widehat{AIE}=2\widehat{BDA}\)
Mà \(\widehat{B}=2\widehat{BDA}\) (cmt)
\(\Rightarrow\widehat{B}=\widehat{AIE}\)
Ta có B và I cùng nhìn AE dưới 2 góc bằng nhau => ABIE là tứ giác nội tiếp
\(\Rightarrow\widehat{BAI}=\widehat{BEI}\) (góc nt cùng chắn cung BI) (1)
Xét tg cân AIE có
\(IK\perp AE\Rightarrow\widehat{AIK}=\widehat{EIK}\) (trong tg cân đường cao XP từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
Xét tg AIC và tg EIC có
IA=IE (cmt); \(\widehat{AIK}=\widehat{EIK}\left(cmt\right)\); IC chung => tg AIC = tg EIC (c.g.c)
\(\Rightarrow\widehat{CAI}=\widehat{BEI}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BAI}=\widehat{CAI}\)

\(\left(x+2\right)^2-\left(2x+1\right)\left(x+2\right)=0\\ < =>\left(x+2\right)\left[\left(x+2\right)-\left(2x+1\right)\right]=0\\ < =>\left(x+2\right)\left(x+2-2x-1\right)=0\\ < =>\left(x+2\right)\left(1-x\right)=0\\ < =>\left[{}\begin{matrix}x+2=0\\1-x=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Vậy: ...
\(\left(x+2\right)^2-\left(2x+1\right)\left(x+2\right)=0\)
=>(x+2)(x+2-2x-1)=0
=>(x+2)(-x+1)=0
=>\(\left[{}\begin{matrix}x+2=0\\-x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

\(42+x^3:5=19\)
=>\(x^3:5=19-42=-23\)
=>\(x^3=-115\)
=>\(x=\sqrt[3]{-115}\)


Đặt \(P=x^3+y^3+z^3-3xyz\)
\(=x^3+\left(y+z\right)^3-3yz\left(y+z\right)-3xyz\)
\(=\left(x+y+z\right)\left[x^2-x\left(y+z\right)+\left(y+z\right)^2\right]-3yz\left(x+y+z\right)\)
\(=3\left(x^2+y^2+z^2+2yz-xy-xz\right)-9yz\)
\(=3\left(x^2+y^2+z^2-xy-yz-zx\right)\)
\(=3\left[\left(x+y+z\right)^2-3\left(xy+yz+zx\right)\right]\)
\(=3\left[9-3\left(xy+yz+zx\right)\right]\)
Do \(0\le x,y,z\le2\Rightarrow\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge0\)
\(\Rightarrow xyz+\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge0\)
\(\Rightarrow2\left(xy+yz+zx\right)-4\left(x+y+z\right)+8\ge0\)
\(\Rightarrow2\left(xy+yz+zx\right)\ge4.3-8=4\)
\(\Rightarrow xy+yz+zx\ge2\)
\(\Rightarrow P\le3.\left[9-3.2\right]=9\)
\(P_{max}=9\) khi \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị của chúng