các bạn ơi tại sao có 1 số lần mình gửi câu trả lời nhưng gửi xong lại biến mất ,dù có làm cách nào nó cũng ko hiện ra vào mục trả lời nhưng vào trang cá nhân lại có .Giải thích tại sao cho mình biết với(các bạn có bị giống mình ko)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


31 tháng 1 2024
-Nếu các bạn gửi câu trả lời thì kèm theo hình vẽ để dễ hiểu hơn nha (không có cũng không sao)
-Mong các bạn trả lời nhanh cho mình nha vì mai mình phải nộp rồi
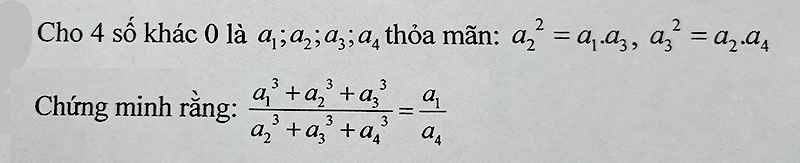


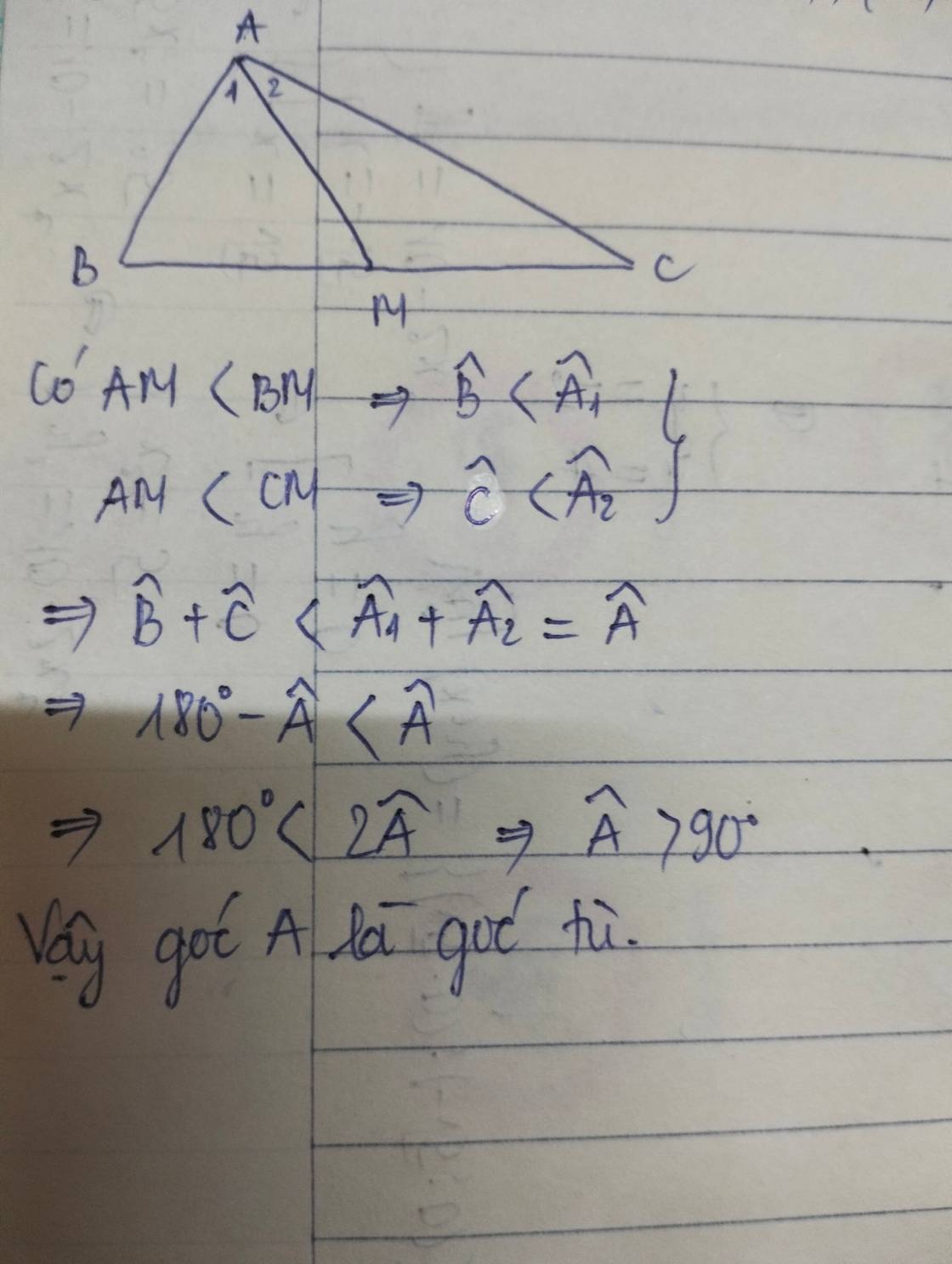

I don't know
mà có bị thật hả?
ừ tôi bị suốt lun