\(\dfrac{x}{x-1}+\dfrac{x-1}{x}=2\)

\(\Leftrightarrow\dfrac{x^2}{x\left(x-1\right)}+\dfrac{\left(x-1\right)^2}{x\left(x-1\right)}=2\)

\(\Leftrightarrow\dfrac{x^2+\left(x-1\right)^2}{x\left(x-1\right)}=2\)

\(\Leftrightarrow\dfrac{x^2+x^2-2x+1}{x\left(x-1\right)}-\dfrac{2x\left(x-1\right)}{x\left(x-1\right)}=0\)

\(\Leftrightarrow\dfrac{2x^2-2x+1-\left(2x^2-2x\right)}{x\left(x-1\right)}=0\)

\(\Leftrightarrow\dfrac{2x^2-2x+1-2x^2+2x}{x\left(x-1\right)}=0\)

\(\Leftrightarrow\dfrac{1}{x\left(x-1\right)}=0\)

\(\Leftrightarrow1=0x\left(x-1\right)\)

\(\Leftrightarrow1=0\)

vậy phương trình không có nghiệm

khoảng cách : `1`

số số hạng là  :`(2050-2021):1+1=30`

tổng là : `(2050 +2021) . 30 :2=61065`

giup tớ 

Vì hai bài giống nhau nên anh sẽ làm mẫu bài 1 nhé.

ko bt lm

\(42\) phút \(=\dfrac{7}{10}\) giờ

Gọi vận tốc của xe thứ nhất là \(a\left(a>0\right)\left(km/h\right)\)

\(\Rightarrow\)Vận tốc của xe thứ hai là \(a-12\left(km/h\right)\)

Theo đề ra, ta có phương trình:

\(\dfrac{270}{a-12}-\dfrac{270}{a}=\dfrac{7}{10}\)

\(\Leftrightarrow\dfrac{1}{a-12}-\dfrac{1}{a}=\dfrac{7}{2700}\)

\(\Leftrightarrow\dfrac{12}{a\left(a-12\right)}=\dfrac{7}{2700}\)

\(\Leftrightarrow7a^2-84a=32400\)

\(\Leftrightarrow7.\left(a-74,29\right)\left(a+62,29\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}7=0\left(l\right)\\a-74,29=0\\a+62,29=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=74,29\left(t/m\right)\\a=-62,29\left(l\right)\end{matrix}\right.\)

\(\Rightarrow a=74,29\)

\(\Rightarrow a-12=74,29-12=62,29\)

Vậy xe thứ nhất đi với vận tốc \(74,29km/h\); xe thứ hai đi với vận tốc \(62,29km/h\).

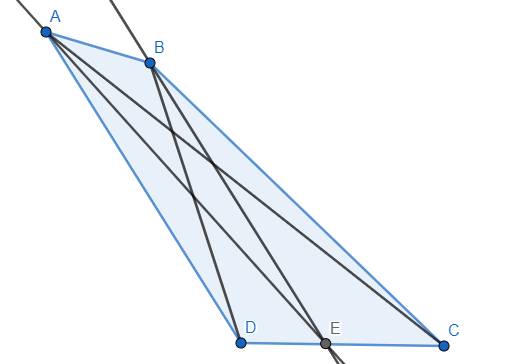
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)