Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- \(x^2\) + 5\(x\) - 4 = 0
-\(x^2\) + \(x\) + 4\(x\) - 4 = 0
(- \(x^2\) + \(x\)) + (4\(x\) - 4) = 0
-\(x\)(\(x-1\)) + 4\(\times\)( \(x\) -1) = 0
(\(x-1\))( -\(x\) +4) = 0
\(\left[{}\begin{matrix}x-1=0\\-x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x\) \(\in\) { 1; 4}
`-x^2+5x-4 =0`
`\Rightarrow x^2-5x+4=0`
`\Rightarrow x^2-4x-x+4=0`
`\Rightarrow (x^2-4x)-(x-4)=0`
`\Rightarrow x(x-4)-(x-4)=0`
`\Rightarrow (x-4)(x-1)=0`
\(\Rightarrow\left[{}\begin{matrix}x-4=0\\x-1=0\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0+4\\x=0+1\end{matrix}\right.\)
``\Rightarrow `\(\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={4; 1}.`

`2x(x-2)=0`
`\rightarrow 2x^2-4x=0`
`\rightarrow x(2x-4)=0`
`\rightarrow `\(\left[{}\begin{matrix}x=0\\2x-4=0\end{matrix}\right.\)
`\rightarrow `\(\left[{}\begin{matrix}x=0\\2x=4\end{matrix}\right.\)
`\rightarrow `\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={0; 2}`
`-x^2+5x-4=0`
`\rightarrow x^2-5x+4=0`
`\rightarrow x^2-4x-x+4=0`
`\rightarrow (x^2-4x)-(x-4)=0`
`\rightarrow x(x-4)-(x-4)=0`
`\rightarrow (x-4)(x-1)=0`
`\rightarrow `\(\left[{}\begin{matrix}x-4=0\\x-1=0\end{matrix}\right.\)
`\rightarrow `\(\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={4; 1}.`

2\(x\)(\(x-2\)) = 0
\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
vậy \(x\) \(\in\) { 0; 2}

\(\dfrac{55-x}{1963}+\dfrac{50-x}{1968}+\dfrac{45-x}{1973}+\dfrac{40-x}{1978}+4=0\)
\(\Rightarrow\text{ }\dfrac{55-x}{1963}+\dfrac{50-x}{1968}+\dfrac{45-x}{1973}+\dfrac{40-x}{1978}+1+1+1+1=0\)
\(\Rightarrow\text{ }\left(\dfrac{55-x}{1963}+1\right)+\left(\dfrac{50-x}{1968}+1\right)+\left(\dfrac{45-x}{1973}+1\right)+\left(\dfrac{40-x}{1978}+1\right)=0\)
\(\Rightarrow\text{ }\dfrac{2018-x}{1963}+\dfrac{2018-x}{1968}+\dfrac{2018-x}{1973}+\dfrac{2018-x}{1978}=0\)
\(\Rightarrow\text{ }\left(2018-x\right)\left(\dfrac{1}{1963}+\dfrac{1}{1968}+\dfrac{1}{1973}+\dfrac{1}{1978}\right)=0\)
Mà \(\dfrac{1}{1963}+\dfrac{1}{1968}+\dfrac{1}{1973}+\dfrac{1}{1978}\ne0\)
\(\Rightarrow\text{ }2018-x=0\)
\(\Rightarrow\text{ }x=2018-0\)
\(\Rightarrow\text{ }x=2018\)
Vậy, \(x=2018.\)

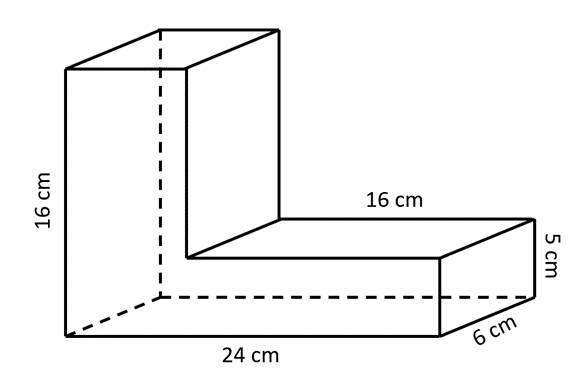
Chừ mình sẽ nối dài chiều dài của phần dưới của hình để được 2 HHCN.
Phần dưới có kích thước 24 x 6 x 5. Phần trên có kích thước là 8 x 6 x 11
a, Phần cần sơn là tổng diện tích toàn phần trừ đi 2 lần diện tích 8 x 6
Diện tích toàn phần HHCN trên:
2 x 8 x 6 + 2 x 11 x (8+6)= 404 (cm2)
Diện tích toàn phần HHCN dưới:
2 x 24 x 6 + 2 x 5 x (6+24)= 438(cm2)
Diện tích bề mặt khối gỗ cần sơn:
404 + 438 - 2 x 8 x 6= 746(cm2)
b, Thể tích phần trên khối gỗ:
8 x 6 x 11= 528(cm3)
Thể tích phần dưới khối gỗ:
24 x 6 x 5 = 720(cm3)
Thể tích của khối gỗ đã cho:
528 + 720 = 1248(cm3)

`6x^2+9=0`
Vì \(x^2\ge0\text{ }\forall\text{ x}\)
`\rightarrow`\(6x^2+9\ge9>0\text{ }\forall\text{ x}\)
`\rightarrow` Đa thức vô nghiệm.
Hoặc nếu bạn chưa hiểu hay chưa quen với cách trên thì bạn có thể sử dụng cách này:
\(6x^2+9=0\)
\(\rightarrow\text{ }6x^2=0-9\)
\(\rightarrow\text{ }6x^2=-9\)
Mà \(x^2\ge0\text{ }\forall\text{ x}\)
\(\rightarrow\text{ Đa thức vô nghiệm.}\)
(Cách này mình chỉ giải ra cho bạn hiểu thôi á, còn nếu mà chứng minh thì mình nghĩ cách làm thứ nhất của mình mới dùng dc á cậu).
Dùng phương pháp phản chứng em nhé:
Giả sử đa thức P(\(x\)) = 6\(x^2\) + 9, có nghiệm thì sẽ tồn tại giá trị của \(x\) để:
6\(x^2\) + 9 = 0
Mặt khác ta có: \(x^2\) ≥ 0 ∀ \(x\) ⇒ 6\(x^2\) ≥ 0 ∀ \(x\) ⇒ 6\(x^2\) + 9 > 9 ∀ \(x\)
vậy 6\(x^2\) + 9 = 0 (là sai) hay
Đa thức: 6\(x^2\) + 9 vô nghiệm (đpcm)
;-; 6,3 chịu r ko đc hsg nha
phải được 6 môn trên 8.0 tbm và 2 môn còn lại trên 6.5 mới được hsg nhé
điểm tbm tiếng anh của bạn là: 6.3 nhé