Lời giải:
Xét tam giác $BMD$ và $EMA$ có:

$\widehat{BMD}=\widehat{EMA}$ (đối đỉnh) 

$BM=EM$ (gt) 

$MD=MA$ (do $M$ là trung điểm $AD$)

$\Rightarrow \triangle BMD=\triangle EMA$ (c.g.c)

$\Rightarrow BD=EA$ (đpcm)

và $\widehat{MBD}=\widehat{MEA}$

Mà 2 góc này ở vị trí so le trong nên $AE\parallel BD$ (đpcm)

Hình vẽ:

  5 + 5 

= năm + năm

= năm x 1 + năm x 1

= năm x ( 1 + 1)

= 2 (năm)

Lời giải:

$=(\frac{3}{5}+\frac{2}{5})+(\frac{5}{11}+\frac{16}{11})+(\frac{7}{13}+\frac{19}{13})$

$=\frac{5}{5}+\frac{22}{11}=\frac{26}{13}=1+2+2=5$

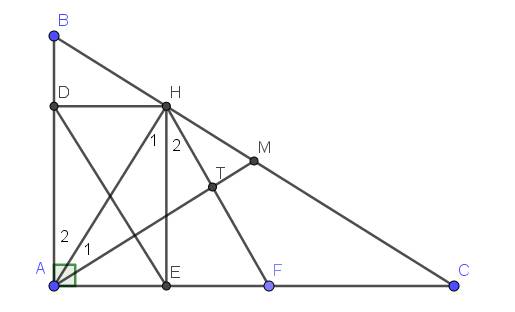
Lời giải:
a. 

Áp dụng định lý Pitago:

$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) 

$AM=\frac{BC}{2}=10:2=5$ (cm) - tính chất đường trung tuyến ứng với cạnh huyền thì bằng 1/2 cạnh huyền.

b.

Tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}$ nên $ADHE$ là hcn

$\Rightarrow AH=DE$.

c.

Do $AM=\frac{BC}{2}=BM$ nên tam giác $MAB$ cân tại $M$

$\Rightarrow \widehat{B}=\widehat{MAB}$

Gọi $T$ là giao điểm $HF$ và $AM$

Do $F$ đối xứng với $A$ qua $E$ nên $E$ là trung điểm của $AF$.

Tam giác $HAF$ có đường cao $HE$ đồng thời là trung tuyến nên $HAF$ cân tại $H$

$\Rightarrow HE$ cũng là đường phân giác.

$\Rightarrow \widehat{H_1}=\widehat{H_2}$

$\Rightarrow \widehat{AHT}=\widehat{H_1}+\widehat{H_2}=2\widehat{H_1}=2\widehat{A_2}=\widehat{A_2}+\widehat{A_2}$

$=\widehat{A_2}+90^0-\widehat{B}=\widehat{A_2}+90^0-\widehat{MAB}=\widehat{A_2}+90^0-(\widehat{A_1}+\widehat{A_2})$

$=90^0-\widehat{A_1}$

Vậy: $\widehat{AHT}+\widehat{A_1}=90^0$

$\Rightarrow \widehat{HTA}=180^0-(\widehat{AHT}+\widehat{A_1})=180^0-90^0=90^0$
$\Rightarrow AM\perp HF$

Hình vẽ:

4 và 3/4 m = 4,75 m                                                 1 và 1/25 m = 1,04 m

2 và 1/2 km = 2,5 km                                           5 và 5/100km= 5,05 km

4m\(\dfrac{3}{4}\) m=\(\dfrac{19}{4}\) =4,75m

1m\(\dfrac{1}{25}\) m=\(\dfrac{26}{25}\)m =1,04m

2km\(\dfrac{1}{2}\) km=\(\dfrac{5}{2}\) km=2,5km

5km\(\dfrac{5}{100}\) km=\(\dfrac{101}{20}\) km=5,05km

:D

Chiều dài mảnh đất:

10 : 2 x 3 = 15 (m)

Diện tích mảnh đất:

15 x 10 = 150 (m²)

Đ.số: diện tích mảnh đất là 150m²

Mọi người giúp mình với, mình không biết câu trả lời của bài trên ạ !

Nếu ai giúp được thì chỉ mình với, mình xin chân thành cảm ơn bạn đó!

     a, Trị giá xuất khẩu (triệu đô la Mỹ)

b, Tổng giá trị xuất khẩu hàng hóa của ngành khai khoáng qua các năm 2018; 2019; 2020; 2021 là:

          3172,1 + 2879 + 2275 + 2506,6 = 10832,7(đô)

c, So với năm 2018 thì năm 2021 giá trị xuất khẩu giảm:

                3172,1 - 2506,6 = 665,5 (đô)

   So với năm 2020 thì giá trị xuất khẩu năm 2021 tăng số phần trăm là:

           (2506,6 - 2275):2257 x100 ≈ 10,2 %

Vậy nhận định của bài báo cáo là đúng

Tổng diện tích các tấm bìa của Bắc:

(43+1) : 2 x 22 = 484(cm²)

Tổng diện tích các tấm bìa của Bình:

(46+2):2 x 23= 552(cm²)

Tổng diện tích các tấm bìa của Bình lớn hơn tổng diện tích các tấm bìa của Bắc là:

552 - 484 = 68(cm²)

Đ.số: 68cm²

Lời giải:
Số được đem nhân với 457 là:

$635,2:(4+5+7)=39,7$

Tích đúng là:

$39,7\times 457=18142,9$

  Vì số đem nhân với 457 lại đặt tích riêng thẳng cột như phép cộng nên thực tế đã đem nhân số đó với 

            4 + 5 + 7  = 16

Số đem nhân là:   635,2 : 16 = 39,7

          Tích đúng là: 39,7 x 457 = 18142,9

đs..