Cho tam giác ABC vuông tại B lấyM là trung điểm của BC trên tia đối của MA lấy điểm D sao cho MD bằng MA
a,so sánh AC bằng CD
B,số sánh AC và CD
C, so sánh góc BAM và góc CAM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2x³ - 5x² + 8x - 3
= 2x³ - x² - 4x² + 2x + 6x - 3
= (2x³ - x²) - (4x² - 2x) + (6x - 3)
= x²(2x - 1) - 2x(2x - 1) + 3(2x - 1)
= (2x - 1)(x² - 2x + 3)

Do là bài tập cũng gọi là dành cho chuyên hơi khó xíu bt học thêm ấy chỗ ẫy cũng khó nên bài tập ít nhưng mà nâng cao

Gọi x (km/h) là vận tốc của ô tô 1 (x > 10)
Vận tốc của ô tô 2 là: x - 10 (km/h)
Thời gian ô tô 1 đi từ A đến B:
 Thời gian ô tô 2 đi từ A đến B:
Thời gian ô tô 2 đi từ A đến B:
 Theo đề bài, ta có phương trình:
Theo đề bài, ta có phương trình:
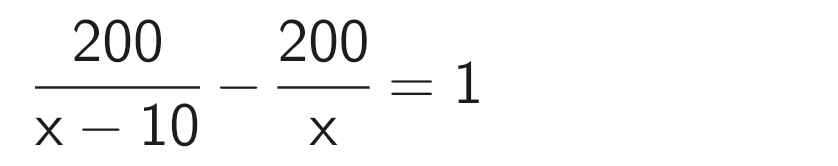 200x - 200(x - 10) = x(x - 10)
200x - 200(x - 10) = x(x - 10)
200x - 200x + 2000 = x² - 10x
x² - 10x - 2000 = 0
x² - 50x + 40x - 2000 = 0
(x² - 50x) + (40x - 2000) = 0
x(x - 50) + 40(x - 50) = 0
(x - 50)(x + 40) = 0
x - 50 = 0 hoặc x + 40 = 0
*) x - 50 = 0
x = 50 (nhận)
*) x + 40 = 0
x = -40 (loại)
Vậy vận tốc của xe ô tô 1 là 50 km/h, vận tốc của xe ô tô 2 là 50 - 10 = 40 km/h

a: \(\left(\dfrac{1}{2}x^5-3x^2\right):x^2-x\left(\dfrac{1}{2}x^2+5\right)+2x\left(x-2\right)\left(x+2\right)-\left(x^3-27\right):\left(x-3\right)\)
\(=\dfrac{1}{2}x^3-3-\dfrac{1}{2}x^3-5x+2x\left(x^2-4\right)-\dfrac{\left(x-3\right)\left(x^2+3x+9\right)}{x-3}\)
\(=-5x-3+2x^3-8x-x^2-3x-9\)
\(=2x^3-x^2-16x-12\)
b: \(\left(7x^3-2x^2\right):\left(-2x^2\right)+\left(\dfrac{5}{4}x^2-3x\right):x-\dfrac{1}{2}x\left(x-1\right)\left(2x+1\right)\)
\(=\dfrac{-7}{2}x+1+\dfrac{5}{4}x-3-\dfrac{1}{2}x\left(2x^2+x-2x-1\right)\)
\(=-\dfrac{9}{4}x-2-\dfrac{1}{2}x\left(2x^2-x-1\right)\)
\(=-\dfrac{9}{4}x-2-x^3+\dfrac{1}{2}x^2+\dfrac{1}{2}x\)
\(=-x^3+\dfrac{1}{2}x^2-\dfrac{7}{4}x-2\)

\(x^2-3x+9=-xy+2y\)
\(\Rightarrow x^2-3x+xy-2y=-9\)
\(\Rightarrow\left(x^2+xy\right)-\left(2x+2y\right)-x=-9\)
\(\Rightarrow x\left(x+y\right)-2\left(x+y\right)-x=-9\)
\(\Rightarrow\left(x-2\right)\left(x+y\right)-x=-9\)
\(\Rightarrow\left(x-2\right)\left(x+y\right)-\left(x-2\right)=-7\)
\(\Rightarrow\left(x-2\right)\left(x+y-1\right)=-7\) (1)
Vì x và y nguyên nên (x-2) và (x+y-1) cũng nguyên (2)
Từ (1) và (2) suy ra:
\(\left(x-2\right);\left(x+y-1\right)\inƯ\left(-7\right)=\left\{\text{±}1;\text{±}7\right\}\)
Sau đó thì bạn lập bảng và kết luận nhé!

\(6x^4+7x^3-37x^2-8x+12\\ =6x^4-3x^3+10x^3-5x^2-32x^2+16x-24x+12\\ =3x^3\left(2x-1\right)+5x^2\left(2x-1\right)-16x\left(2x-1\right)-12\left(2x-1\right)\\ =\left(2x-1\right)\left(3x^3+5x^2-16x-12\right)\\ =\left(2x-1\right)\left(3x^3-6x^2+11x^2-22x+6x-12\right)\\ =\left(2x-1\right)\left[3x^2\left(x-2\right)+11x\left(x-2\right)+6\left(x-2\right)\right]\\ =\left(2x-1\right)\left(x-2\right)\left(3x^2+11x+6\right)\\ =\left(2x-1\right)\left(x-2\right)\left(3x^2+9x+2x+6\right)\\ =\left(2x-1\right)\left(x-2\right)\left[3x\left(x+3\right)+2\left(x+3\right)\right]\\ =\left(2x-1\right)\left(x-2\right)\left(x+3\right)\left(3x+2\right)\)

\(x^4+x^3+2x^2+x+1\\= x^4+x^3+x^2+x^2+x+1\\ =x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^2+1\right)\left(x^2+x+1\right)\)
a,b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{BMA}=\widehat{CMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMBA=ΔMCD
=>AB=CD
mà AB<AC
nên CD<AC
c: ΔMBA=ΔMCD
=>\(\widehat{MAB}=\widehat{MDC}\left(1\right)\)
Xét ΔCDA có CD<CA
mà \(\widehat{CAD};\widehat{CDA}\) lần lượt là góc đối diện của các cạnh CD,CA
nên \(\widehat{CAD}< \widehat{CDA}\)(2)
Từ (1),(2) suy ra \(\widehat{CAD}< \widehat{MAB}\)