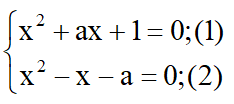Cho đường tròn \(\left(\omega\right)\), B là 1 điểm trên \(\left(\omega\right)\). Trên tiếp tuyến tại B của \(\left(\omega\right)\) lấy điểm A. Lấy điểm C sao cho đoạn AC cắt \(\left(\omega\right)\) tại 2 điểm phân biệt. Đường tròn \(\left(\omega'\right)\) tiếp xúc AC tại C, tiếp xúc \(\left(\omega\right)\) tại D, sao cho D khác phía B đối với AC. CMR tâm đường tròn ngoại tiếp tam giác BCD nằm trên đường tròn ngoại tiếp tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(C=sin50+sin60+sin70-sin70-sin60-sin50=0\)
\(D=tan20.\left(-tan70\right).tan30=cot70\left(-tan70\right)tan30=-tan30=-\dfrac{\sqrt{3}}{3}\)

(*) \(N=\left\{1;3;5;7\right\}\)
\(N=\left\{x\inℕ^∗|x⋮̸2;x\le7\right\}\)
(*) \(M=\left\{1;4;9;16;25\right\}\)
\(M=\left\{x|x=k^2;k\inℕ^∗;k\le5\right\}\)

Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: phương trình này vô nghiệm
vì
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.
5ttttttttttttttttttttttttttttttttttttttttttttttttvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv555555555555555555555555555555555bbbnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

khi thay y(x) = -y(-x) là hàm số lẽ .
Bài 7 làm chuẩn, có :
\(\left|4x+3\right|-\left|4x-3\right|=\left|-4x+3\right|-\left|-4x-3\right|\)
\(\left|4x+3\right|-\left|4x-3\right|=\left|4x-3\right|-\left|4x+3\right|\)
\(\left|4x+3\right|-\left|4x-3\right|=-\left|4x+3\right|+\left|4x-3\right|\)
Kết quả:
1. hàm lẽ
2. hàm lẽ
3. hàm chẵn
4. hàm lẽ
5. hàm chẵn (đem ra ngoài căn và chia được.)
6. hàm chẵn
7. hàm lẽ
8. hàm chẵn
9. hàm lẽ
10. hàm lẽ, bạn vẽ hình nhé như chữ z nhưng z vuông , trong trục tọa độ theo đinh nghĩa đối xứng qua gốc
11. hàm lẽ , hình vẽ như Z . Bạn dùng geogebra vẽ hai đường y = x-5 và y =x+5, tô màu đỏ các phần đường bạn chấp nhận.
tiếp theo cho bài 11
bạn vẽ hình thì các điểm có tọa độ (x,y) nằm trên đường màu đen, bạn tô màu đỏ cho dễ nhìn, thấy đối xứng qua O, quay 180 độ thì trùng lên nhau

Mỗi bài bạn chỉ nên đăng 1 lần thôi. Tránh đăng lặp lại nhiều gây loãng box toán.

Vì đây là câu hỏi trắc nghiệm nên chỉ cần thử từng giá trị là ra thôi, nhưng ai lại làm như thế cho mất công?
Gọi \(x\) là số lần cần cắt theo cách 1 \(\left(x\inℕ\right)\)
và \(y\) là số lần cần cắt theo cách 2 \(\left(y\inℕ\right)\)
Nếu cắt theo cách 1, \(x\) lần cắt sẽ cho ra \(3x\) hộp B1, \(x\) hộp cao Sao vàng và \(6x\) hộp Quy sâm.
Nếu cắt theo cách 2, \(y\) lần cắt sẽ cho ra \(2y\) hộp B1, \(3y\) hộp cao Sao vàng và \(y\) hộp Quy sâm.
Số hộp Quy sâm phải có là 900 hộp nên ta có \(6x+y=900\).
Số hộp B1 tối thiểu là 900 hộp, do đó \(3x+2y\ge900\)
Số hộp cao Sao vàng tối thiểu là 1000 hộp nên \(x+3y\ge1000\)
Do đó ta có hệ \(\left\{{}\begin{matrix}6x+y=900\left(!\right)\\3x+2y\ge900\left(@\right)\\x+3y\ge1000\left(\&\right)\end{matrix}\right.\) với \(x,y\inℕ\)
\(\left(\&\right)\Leftrightarrow3x+9y\ge3000\) (*)
Từ \(\left(@\right)\) và (*) \(\Leftrightarrow3x+9y-\left(3x+2y\right)\ge2100\) \(\Leftrightarrow7y\ge2100\Leftrightarrow y\ge300\). Ta thấy trong 4 phương án không tồn tại phương án nào có \(y>300\) nên ta sẽ cho \(y=300\) (thi tự luận không được làm vậy đâu nhé bạn)
(đến đây ta có thể loại 2 lựa chọn B và D vì \(y< 300\))
Nếu \(y=300\) thì \(900-6x=300\) \(\Leftrightarrow6x=600\) \(\Leftrightarrow x=100\)
Như vậy để tổng số tấm bìa phải dùng là ít nhất (mà vẫn hợp lệ) thì ta sẽ chọn A.