Cho tam giác ABC vuông tại C có góc A < gócB . Gọi I, O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp tam
giác ABC. Biết rằng tam giác BIO vuông. Tính tỉ số các cạnh của tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai đường chéo AC,BD cắt nhau tại H .Trong tam giác vuông ABD ,ta có :
\(\frac{HD}{HB}=\frac{AD^2}{AB^2}=\frac{4^2}{6^2}=\frac{4}{6}\)
Dễ thấy \(\Delta HDC~\Delta HBA\)nên
\(\frac{DC}{AB}=\frac{HD}{HB}\)\(=\frac{4}{9}\)\(\Rightarrow\)\(DC\)=\(\frac{4}{9}.6=\frac{8}{3}\)(Cm)
Kẻ đường cao CK của tam giác ABC , dễ thấy KB = AB - DC = 6 -\(\frac{8}{3}\)=\(\frac{10}{3}\)
\(\Rightarrow\)\(BC=\frac{\sqrt{224}}{3}=\frac{2\sqrt{61}}{3}\left(cm\right)\)

\(\left(2x+1\right)\left(x+1\right)\left(3x-2\right)\left(6x-7\right)+4=0\)
\(\Leftrightarrow\left[\left(2x+1\right)\left(3x-2\right)\right]\left[\left(x+1\right)\left(6x-7\right)\right]+4=0\)
\(\Leftrightarrow\left(6x^2-x-2\right)\left(6x^2-x-7\right)+4=0\)
\(\Leftrightarrow\left(6x^2-x\right)^2-9\left(6x^2-x\right)+14+4=0\)
\(\Leftrightarrow\left(6x^2-x\right)^2-6\left(6x^2-x\right)-3\left(6x^2-x\right)+18=0\)
\(\Leftrightarrow\left(6x^2-x-6\right)\left(6x^2-x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}6x^2-x-6=0\\6x^2-x-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1\pm\sqrt{145}}{2}\\x=\frac{1\pm\sqrt{73}}{12}\end{cases}}\)

Để đồ thị hàm số \(y=\left(2m+2\right)x-5m\)song song với đường thẳng \(y=4x+1\)thì:
\(\hept{\begin{cases}2m+2=4\\-5m\ne1\end{cases}}\Leftrightarrow m=1\).


\(A=\sqrt{5-2\sqrt{6}}=\sqrt{3-2\sqrt{3}.\sqrt{2}+2}=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{3}-\sqrt{2}\right|=\sqrt{3}-\sqrt{2}\)
\(B=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}\)
\(\sqrt{2}B=\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}=\sqrt{5-2\sqrt{5}+1}-\sqrt{5+2\sqrt{5}+1}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}=\left|\sqrt{5}-1\right|-\left|\sqrt{5}+1\right|\)
\(=\sqrt{5}-1-\left(\sqrt{5}+1\right)=-2\)

a)\(\sqrt{4x+20}\) +\(\sqrt{x-5}\) -\(\dfrac{1}{3}\)\(\sqrt{9x-45}\)=4 ; ĐKXĐ : x ≥_+ 5
⇔ \(\sqrt{2^2x+2^2.5}\) +\(\sqrt{x-5}\) -\(\dfrac{1}{3}\)\(\sqrt{3^2x-3^2.5}\) =4
⇔ 2\(\sqrt{x+5}\) +\(\sqrt{x-5}\) -\(\dfrac{1}{3}\)3\(\sqrt{x-5}\) =4 ⇔ 2\(\sqrt{x+5}\) +\(\sqrt{x-5}\) -\(\sqrt{x-5}\) =4⇔2\(\sqrt{x+5}\)=4(tm)
⇔\(\sqrt{x+5}\)=2⇔x+5=4 ⇔x=-1
Vậy x=-1
b) \(\sqrt{x^2-36}\) - \(\sqrt{x-6}\) =0 ; ĐKXĐ: x≥_+6
⇔ \(\sqrt{\left(x-6\right)\left(x+6\right)}\) - \(\sqrt{x-6}\) =0 ⇔ \(\sqrt{x-6}\).\(\sqrt{x+6}\) - \(\sqrt{x-6}\) =0
⇔ \(\sqrt{x-6}\)(\(\sqrt{x+6}\) -1 )=0 ⇔\([\) \(\begin{matrix}\sqrt{x-6}&=0\\\sqrt{x+6}-1&=0\end{matrix}\) ⇔ \([\) \(\begin{matrix}x-6&=0\\x+6-1&=0\end{matrix}\) ⇔\([\) \(\begin{matrix}x&=6\left(ktm\right)\\x&=-5\left(tm\right)\end{matrix}\)
Vậy x=-5
c) \(\sqrt{4-x^2}\) -x +2 =0 ; ĐKXĐ: -2≤x≤2
⇔ \(\sqrt{\left(2-x\right)\left(2+x\right)}\) -x+2 =0 ⇔ \(\sqrt{\left(2-x\right)\left(2+x\right)}\) -(x-2)=0
⇔ \(\sqrt{\left(2-x\right)\left(2+x\right)}\) =(x-2) ⇔ (2-x)(2+x)=(x-2)2 ⇔ 4-x2 = x2-4x+4 ⇔ -x2-x2+4x=4-4
⇔-2x2+4x=0 ⇔ -2x(x-2)=0 ⇔ \([\) \(\begin{matrix}-2x&=0\\x-2&=0\end{matrix}\) ⇔\([\) \(\begin{matrix}x&=0\left(tm\right)\\x&=2\left(tm\right)\end{matrix}\)
Vậy S=\(\left\{0;2\right\}\)
d) \(\sqrt{\left(2x-3\right)\left(x-1\right)}-\sqrt{x-1}=0\) ; ĐKXĐ: x≥\(\dfrac{3}{2}\);x ≥ 1
⇔\(\sqrt{2x-3}.\sqrt{x-1}-\sqrt{x-1}=0\) ⇔ \(\sqrt{x-1}.\left(\sqrt{2x-3}-1\right)=0\)
⇔ \(\left[{}\begin{matrix}\sqrt{x-1}=0\\\sqrt{2x-3}-1=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x-1=0\\2x-3-1=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=1\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
Vậy s=\(\left\{1:2\right\}\)

Bài I:
a) Khi \(x=9\):
\(A=\frac{\sqrt{9}+4}{\sqrt{9}-1}=\frac{3+4}{3-1}=\frac{7}{2}\)
b) \(B=\frac{3\sqrt{x}+1}{x+2\sqrt{x}-3}-\frac{2}{\sqrt{x}+3}=\frac{3\sqrt{x}+1}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}-\frac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{3\sqrt{x}+1-2\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\frac{1}{\sqrt{x}-1}\)
c) \(\frac{A}{B}=\frac{\sqrt{x}+4}{\sqrt{x}-1}\div\frac{1}{\sqrt{x}-1}=\sqrt{x}+4\ge\frac{x}{4}+5\)
\(\Leftrightarrow x-4\sqrt{x}+4\le0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)^2\le0\)
\(\Leftrightarrow\sqrt{x}-2=0\)
\(\Leftrightarrow x=4\).

Câu 1: Cho số thực a > 0. Số nào sau dây là căn bậc hai số học của a?
Lời giải:
Với số dương a, số √a được gọi là căn bậc hai số học của a
Đáp án cần chọn là: A
Câu 2: Cho số thực a > 0. Căn bậc hai số học của a là x khi và chỉ khi
Lời giải:
Với số dương a, số x được gọi là căn bậc hai số học của a khi và chỉ khi
Đáp án cần chọn là: D
Câu 3: Số bào sau đây là căn bậc hai số học của số a = 0,36
A. – 0,6
B. 0,6
C. 0,9
D. – 0,18
Lời giải:
Căn bậc hai số học của a = 0,36 là √0,36 = 0,6
Đáp án cần chọn là: B
Câu 4: Số nào sau đây là căn bậc hai số học của số a = 2,25
A. – 1,5 và 1,5
B. 1,25
C. 1,5
D. – 1,5
Lời giải:
Căn bậc hai số học của a = 2,25 là √2,25 = 1,5
Đáp án cần chọn là: C
Câu 5: Khẳng định nào sau đây là đúng?
Lời giải:
Đáp án cần chọn là: C
HT nhé ông bn

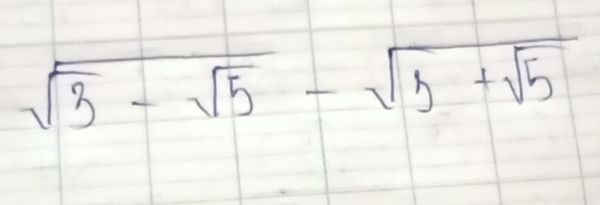



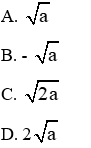
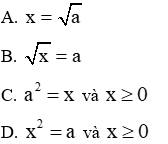
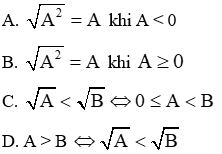
I là tâm đường tròn nội tiếp tam giác và E là tiếp điểm
nên IE⊥AC, mà A^=90o suy ra IE//AB
⇒ANEI=AMEM
⇒AN=AM.EIEM=AC.EI2(AM−AE) (1)
Tứ giác AEIF là hình vuông nên AE=EI;
D, E, F là các tiếp điểm
⇒AE+CD+BD=12(BC+CA+AB)⇒AE=AC+AB−BC2,
thay vào (1) ta được ...
TL:
BC2 nha bạn
HT