\(\dfrac{x+23}{2021}+\dfrac{x+22}{2022}+\dfrac{x+21}{2023}+\dfrac{x+20}{2024}=-4\)

Vì \(\dfrac{x+23}{2021}+\dfrac{x+22}{2022}+\dfrac{x+21}{2023}+\dfrac{x+20}{2024}=-4\)

\(\Rightarrow\dfrac{x+23}{2021}+\dfrac{x+22}{2022}+\dfrac{x+21}{2023}+\dfrac{x+20}{2024}+4=0\)

\(\Rightarrow\left(\dfrac{x+23}{2021}+1\right)+\left(\dfrac{x+22}{2022}+1\right)+\left(\dfrac{x+21}{2023}+1\right)+\left(\dfrac{x+20}{2024}+1\right)=0\)

\(\Rightarrow\dfrac{x+2044}{2021}+\dfrac{x+2044}{2022}+\dfrac{x+2044}{2023}+\dfrac{x+2044}{2024}=0\)

\(\Rightarrow\left(x+2044\right)\left(\dfrac{1}{2021}+\dfrac{1}{2022}+\dfrac{1}{2023}+\dfrac{1}{2024}\right)=0\)

\(\Rightarrow x+2044=0\left(\dfrac{1}{2021}+\dfrac{1}{2022}+\dfrac{1}{2023}+\dfrac{1}{2024}\ne0\right)\)

\(\Rightarrow x=-2024\)

`@` `\text {Ans}`

`\downarrow`

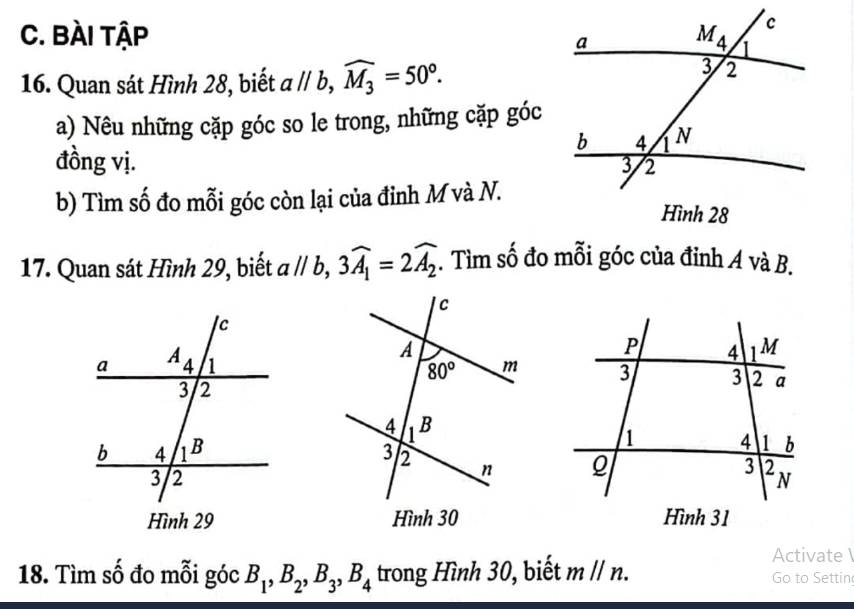
`16,`

`@` Các cặp góc đồng vị:

`+`\(\widehat {M_4}\) và \(\widehat {N_4}\)

`+`\(\widehat {M_1}\) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_2}\)

`+`\(\widehat {M_3}\) và \(\widehat {N_3}\)

`@` Các cặp góc sole trong:

`+`\(\widehat {M_3} \) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_4}\) 

`b,`

Ta có: \(\widehat {M_3} = \widehat {M_1} (\text {đối đỉnh})\)

`=>`\(\widehat {M_1}=50^0\)

\(\widehat {M_3}+\widehat {M_2}=180^0 (\text {kề bù})\)

`=>`\(50^0+\widehat {M_2}=180^0\)

`=>`\(\widehat {M_2}=180^0-50^0=130^0\)

\(\widehat {M_2}=\widehat {M_4} (\text {2 góc đối đỉnh})\)

`=>`\(\widehat {M_4} = 130^0\)

Vì \(\widehat {M_3}\) và \(\widehat {N_1}\) là `2` góc sole trong

`=>`\(\widehat {M_3}=\widehat {N_1}=50^0\)

\(\widehat {M_3}=\widehat {N_3}=50^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_2}=130^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_4}=130^0 (\text {2 góc slt})\)

`17,`

Vì \(\widehat {A_1}\) và \(\widehat {A_2}\) là `2` góc kề bù

`=>`\(\widehat {A_1}+\widehat {A_2}=180^0\)

\(3\widehat {A_1}=2\widehat {A_2}\) (gt)

`=>`\(\widehat{A_1}=\dfrac{2}{3}\cdot\widehat{A_2}\)

Thay \(\widehat{A_1}=\dfrac{2}{3}\widehat{A_2}\)

\(\dfrac{2}{3}\cdot\widehat{A_2}+\widehat{A_2}=180^0\)

`=>`\(\widehat{A_2}\left(\dfrac{2}{3}+1\right)=180^0\)

`=>`\(\widehat{A_2}\cdot\dfrac{5}{3}=180^0\)

`=>`\(\widehat{A_2}=180^0\div\dfrac{5}{3}\)

`=>`\(\widehat{A_2}=108^0\)

Vậy, số đo \(\widehat{A_2}=108^0\)

\(\widehat {A_1}+\widehat {A_2}=180^0 (\text {kề bù})\)

`=>`\(\widehat{A_1}+108^0=180^0\)

`=>`\(\widehat{A_1}=72^0\)

\(\widehat {A_1}=\widehat {A_3}=72^0 (\text {đối đỉnh})\)

\(\widehat {A_2}=\widehat {A_4}=108^0 (\text {đối đỉnh})\)

`@` Số đo các góc của đỉnh B:

`+`\(\widehat {A_4}=\widehat {B_4}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_2}=\widehat {B_2}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_3}=\widehat {B_1}=72^0 (\text {sole trong})\)

`+`\(\widehat {A_3}=\widehat {B_3}=72^0 (\text {đồng vị})\)

\(x+\dfrac{5}{2}=-\dfrac{1}{7}\)

\(\Rightarrow x=-\dfrac{1}{7}-\dfrac{5}{2}\)

\(\Rightarrow x=-\dfrac{2}{14}-\dfrac{35}{14}\)

\(\Rightarrow x=\dfrac{-2-35}{14}\)

\(\Rightarrow x=\dfrac{-37}{14}\)

A              =       1 + 2 + 2² + 2³  + ...+ 2¹⁰⁰

A\(\times\)2         =             2  + 2² + 2³ +...+ 2¹⁰⁰ + 2¹⁰¹

A \(\times\)2 - A   =      2¹⁰¹ - 1

A              =       2¹⁰¹ - 1

Đoạn 2x-1/3 là $\frac{2x-1}{3}$ hay $2x-\frac{1}{3}$ vậy bạn?

`@` `\text {Ans}`

`\downarrow`

\(\dfrac{8^{14}}{4^4\cdot64^5}\)

`=`\(\dfrac{2^{42}}{2^8\cdot2^{30}}\)

`=`\(\dfrac{2^{42}}{2^{38}}=2^4=16\)

\(\dfrac{9^{10}\cdot27^7}{81^7\cdot3^{15}}\)

`=`\(\dfrac{3^{20}\cdot3^{21}}{3^{28}\cdot3^{15}}\)

`=`\(\dfrac{3^{41}}{3^{43}}\)

`=`\(\dfrac{1}{3^2}=\dfrac{1}{9}\)

\(\left(\dfrac{3}{10}\right)^4\cdot\left(0,3\right)^5\cdot\left(\dfrac{10}{3}\right)^{10}\)

`=`\(\left(\dfrac{3}{10}\right)^4\cdot\left(\dfrac{3}{10}\right)^5\cdot\left(\dfrac{10}{3}\right)^{10}\)

`=`\(\left(\dfrac{3}{10}\right)^9\cdot\left(\dfrac{10}{3}\right)^{10}=\dfrac{10}{3}\)

\(\dfrac{\left(4^3\right)^2\cdot9^4}{6^7\cdot8^2}\)

`=`\(\dfrac{\left(2^6\right)^2\cdot3^8}{2^7\cdot3^7\cdot2^9}\)

`=`\(\dfrac{2^{12}\cdot3^8}{2^{16}\cdot3^7}\)

`=`\(\dfrac{3}{2^4}=\dfrac{3}{16}\)

\(\dfrac{4^8\cdot9^4}{6^6\cdot8^3}\)

`=`\(\dfrac{2^{16}\cdot3^8}{2^6\cdot3^6\cdot2^9}\)

`=`\(\dfrac{2^{16}\cdot3^8}{2^{15}\cdot3^6}=2\cdot3^2=18\)

\(3^6\cdot\left(\dfrac{1}{3}\right)^6\cdot81^2\cdot\dfrac{1}{27^2}\)

`=`\(\left(3\cdot\dfrac{1}{3}\right)^6\cdot\dfrac{81^2}{27^2}\)

`=`\(1^6\cdot\dfrac{3^8}{3^6}=1\cdot3^2=9\)

`\text {#KaizuulvG}`

\(\left(3x-5\right)\left(x+\dfrac{1}{2}\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}3x-5=0\\x+\dfrac{1}{2}=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}3x=5\\x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Vậy \(S=\left\{\dfrac{5}{3};-\dfrac{1}{2}\right\}\)

a) Theo đề f(x) nhận -2 là nghiệm lấy -2 thay vào x ta có:

\(\left(-2\right)^2-2m+2=0\)

\(\Rightarrow4-2m+2=0\)

\(\Rightarrow6-2m=0\)

\(\Rightarrow2m=6\)

\(\Rightarrow m=3\)

b) Tìm được m ta có: \(f\left(x\right)=x^2+3x+2\)

\(\Rightarrow x^2+3x+2=0\)

\(\Rightarrow x^2+2x+x+2=0\)

\(\Rightarrow x\left(x+2\right)+\left(x+2\right)=0\)

\(\Rightarrow\left(x+2\right)\left(x+1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)

Vậy tập nghiệm của f(x) là: \(S=\left\{-2;-1\right\}\)