Bài 1:So Sánh
a)3^12 và 5^8 b (0,6)^9 và (-0,9)^6
Bài 2:
a)31^5 và 17^7 b)8^12 và 12^8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

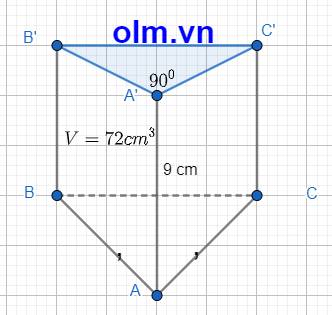
VABCA'B'C' = SABC.h
Diện tích của tam giác ABC là: 72 : 9 = 8 (cm2)
SABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB2 = 8 ⇒ AB2 = 8.2 = 16
⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)
Vậy độ dài cạnh đáy AB dài 4cm

Gọi số ti vi mỗi loại mà cửa hàng bán được lần lượt là:
\(x;y;z\) (chiếc) \(x;y;z\) \(\in\)N*
Thì số tiền thu được được việc bán mỗi loại ti vi lần lượt là:
20\(x;\) 18\(y\); 15\(z\)
Theo bài ra ta có: 20\(x\) = 18\(y\) = 15\(z\); \(x+y+z=62\)
⇒ \(y\) = \(\dfrac{20}{18}\)\(x\) = \(\dfrac{10}{9}\)\(x\)
z = \(\dfrac{20}{15}\)\(x\) = \(\dfrac{4}{3}x\)
⇒ \(x+\dfrac{10}{9}x+\dfrac{4}{3}x=62\)
\(x\left(1+\dfrac{10}{9}+\dfrac{4}{3}\right)=62\)
\(\dfrac{31}{9}\)\(x\) = 62
\(x\) = 62: \(\dfrac{31}{9}\)
\(x\) = 18
\(y\) = \(\dfrac{10}{9}.18=20\)
\(z=\dfrac{4}{3}.18=24\)
Kết luận: Ti vi sam sung bán được 18 chiếc
Ti vi LG bán được 20 chiếc
Ti vi Xiaomi bán được 24 chiếc

Tổng số con cá mà cả ba bạn câu được là:
11 + 9 + 12 = 32 ( con )
Mỗi con cá có mệnh giá là:
192000 : 32 = 6000 ( đồng )
An nhận được số tiền là :
6000 x 11 = 66000 ( đồng )
Bình nhận được số tiền là:
6000 x 9 = 54000 ( dồng )
Cường nhận được số tiền là:
6000 x 12 = 72 000 ( đồng )
Đ/S..
Gọi số tiền mỗi bạn nhận được là \(a,b,c\) ) đồng, \(a,b,c\inℕ^∗\)
Vì số tiền chia tỉ lệ với số con cá câu được nên ta có:
\(\dfrac{a}{11}=\dfrac{b}{9}=\dfrac{c}{12}\) và \(a+b+c=192000\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{11}=\dfrac{b}{9}=\dfrac{c}{12}=\dfrac{a+b+c}{11+9+12}=\dfrac{192000}{32}=6000\)
=> \(\dfrac{a}{11}=6000\Rightarrow a=6000\times11=66000\left(TMĐK\right)\)
=> \(\dfrac{b}{9}=6000\Rightarrow6000\times9=54000\left(TMĐK\right)\)
=> \(\dfrac{c}{12}=6000\Rightarrow c=6000\times12=72000\left(TMĐK\right)\)
Vậy số tiền mỗi bạn An, Bình, Cường nhận được là: 66000 đồng, 54000 đồng, 72000 đồng

6xy+4x-3y=8
=> 6xy -3y=8-4x
=>3y(2x-1)= -2(2x-1) +6
=>(2x-1)(3y+2)=6
mà x,y thuộc Z =>(2x-1),(3y+2) thuộc Z =>(2x-1),(3y+2) thuộc U(6) xong giải ra bình thường nhé mấy câu sau tương tự

a, (3 - \(x\))(4y + 1) = 20
Ư(20) = { -20; -10; -5; -4; -2; -1; 1; 2; 4; 5; 10; 20}
Lập bảng ta có:
| \(3-x\) | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| \(x\) | 23 | 13 | 8 | 7 | 5 | 4 | 2 | 1 | -1 | -2 | -7 | -17 |
| 4\(y\) + 1 | -1 | -2 | -4 | -5 | -10 | -20 | 20 | 10 | 5 | 4 | 2 | 1 |
| \(y\) | -1/2 | -3/4 | -5/4 | -6/4 | -11/4 | -21/4 | 19/4 | 9/4 | 1 | 3/4 | 1/4 | 0 |
Vậy các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) =(-1; 1); (-17; 0)
b, \(x\left(y+2\right)\)+ 2\(y\) = 6
\(x\) = \(\dfrac{6-2y}{y+2}\)
\(x\in\) Z ⇔ 6 - \(2y⋮\) \(y\) + 2 ⇒-(2y + 4) +10 ⋮ \(y\) + 2 ⇒ -2(\(y\)+2) +10 ⋮ \(y\)+2
⇒ 10 ⋮ \(y\) + 2
Ư(10) = { -10; -5; -2; -1; 1; 2; 5; 10}
Lập bảng ta có:
| \(y+2\) | -10 | -5 | -2 | -1 | 1 | 2 | 5 | 10 |
| \(y\) | -12 | -7 | -4 | -3 | -1 | 0 | 3 | 8 |
| \(x=\) \(\dfrac{6-2y}{y+2}\) | -3 | -4 | -7 | -12 | 8 | 3 | 0 | -1 |
Theo bảng trên ta có các cặp \(x;y\)
nguyên thỏa mãn đề bài lần lượt là:
(\(x;y\) ) =(-3; -12); (-4; -7); (-12; -3); (8; -1); (3; 0); (0;3 (-1; 8)

`a)` Xét tử số phân số M :
\(2012-\dfrac{1}{9}-\dfrac{2}{10}-\dfrac{3}{11}-...-\dfrac{2012}{2020}\\ =\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{2}{10}\right)+\left(1-\dfrac{3}{11}\right)+...+\left(1-\dfrac{2012}{2020}\right)\\ =\dfrac{8}{9}+\dfrac{8}{10}+\dfrac{8}{11}+...+\dfrac{8}{2020}\\ =24\left(\dfrac{1}{27}+\dfrac{1}{30}+\dfrac{1}{33}+...+\dfrac{1}{6060}\right)\)
Ta được : \(M=\dfrac{24\left(\dfrac{1}{27}+\dfrac{1}{30}+\dfrac{1}{33}+...+\dfrac{1}{6060}\right)}{\dfrac{1}{27}+\dfrac{1}{30}+\dfrac{1}{33}+...+\dfrac{1}{6060}}=24\)
`b)` Xét tử số phân số N :
\(\dfrac{1}{1.300}+\dfrac{1}{2.301}+\dfrac{1}{3.302}+...+\dfrac{1}{101.400}\\ =\dfrac{1}{299}.\left(\dfrac{299}{1.300}+\dfrac{299}{2.301}+\dfrac{299}{3.302}+...+\dfrac{299}{101.400}\right)\\ =\dfrac{1}{299}.\left(1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+\dfrac{1}{3}-\dfrac{1}{302}+...+\dfrac{1}{101}-\dfrac{1}{400}\right)\)
Xét mẫu số phân số N :
\(\dfrac{1}{1.102}+\dfrac{1}{2.103}+\dfrac{1}{3.104}+...+\dfrac{1}{299.400}\\ =\dfrac{1}{101}.\left(\dfrac{101}{1.102}+\dfrac{101}{2.103}+\dfrac{101}{3.104}+...+\dfrac{101}{299.400}\right)\\ =\dfrac{1}{101}.\left(1-\dfrac{1}{102}+\dfrac{1}{2}-\dfrac{1}{103}+\dfrac{1}{3}-\dfrac{1}{104}+...+\dfrac{1}{299}-\dfrac{1}{400}\right)\)
\(=\dfrac{1}{101}.\left(1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+\dfrac{1}{3}-\dfrac{1}{302}+...+\dfrac{1}{101}-\dfrac{1}{400}\right)\)
Ta được: \(N=\dfrac{\dfrac{1}{299}\left(1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+\dfrac{1}{3}-\dfrac{1}{302}+...+\dfrac{1}{101}-\dfrac{1}{400}\right)}{\dfrac{1}{101}\left(1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+\dfrac{1}{3}-\dfrac{1}{302}+...+\dfrac{1}{101}-\dfrac{1}{400}\right)}\\ =\dfrac{\dfrac{1}{299}}{\dfrac{1}{101}}=\dfrac{101}{299}\)

\(\dfrac{\left(x+3\right)}{7}+\dfrac{\left(x+4\right)}{6}+\dfrac{\left(x+90\right)}{10}+3=0\\ \Leftrightarrow\dfrac{60\left(x+3\right)}{420}+\dfrac{70\left(x+4\right)}{420}+\dfrac{42\left(x+90\right)}{420}+\dfrac{1260}{420}=0\\ \Leftrightarrow60x+180+70x+280+42x+3780+1260=0\\ \Leftrightarrow172x=-5500\\ \Leftrightarrow x=-\dfrac{1375}{43}\)
`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
`3^12` và `5^8`
\(3^{12}=\left(3^3\right)^4=9^4\)
\(5^8=\left(5^2\right)^4=25^4\)
Vì `9 < 25` `=> 25^4 > 9^4`
`=> 3^12 > 5^8`
Vậy, `3^12 > 5^8`
`b)`
`(0,6)^9` và `(-0,9)^6`
\(\left(0,6\right)^9=\left(0,6^3\right)^3=\left(0,216\right)^3\)
\(\left(-0,9\right)^6=\left[\left(-0,9\right)^2\right]^3=\left(0,81\right)^3\)
Vì `0,81 > 0,216 => (0,81)^3 > (0,216)^3`
`=> (0,6)^9 < (-0,9)^6`
Vậy, `(0,6)^9<(-0,9)^6`
1.a) Có 312 = 33.4 = 274 ;
58 = 52.4 = 254
Dễ thấy 274 > 254 nên 312 > 58
b) Có \(0,6^9=\dfrac{6^9}{10^9}=\dfrac{6^{3.3}}{10^9}=\dfrac{216^3}{10^9}\)
mà \(\left(-0,9\right)^6=0,9^6=\dfrac{9^6}{10^6}=\dfrac{9^6.10^3}{10^9}=\dfrac{9^{2.3}.10^3}{10^9}=\dfrac{81^3.10^3}{10^9}=\dfrac{810^3}{10^9}\)
Dễ thấy \(\dfrac{216^3}{10^9}< \dfrac{810^3}{10^9}\Rightarrow0,6^9< \left(-0,9\right)^6\)