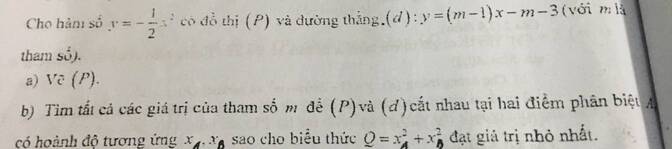`(P):y=x^2`     `(d):y=4x+1-m`

Xét ptr hoành độ của `(P)` và `(d)` có:

    `x^2=4x+1-m`

`<=>x^2-4x-1+m=0`

    Mà `m=4`

  `=>x^2-4x-1+4=0`

`<=>x^2-4x+3=0`

`<=>x^2-3x-x+3=0`

`<=>(x-3)(x-1)=0`

`<=>x=3` hoăc `x=1`

Vậy hoành độ giao điểm của `(P)` và `(d)` là: `x=3;x=1`

(P)=x đúng ko vậy

\(A^2=x+2\sqrt{2x-4}+x-2\sqrt{2x-4}+2\sqrt{\left(x+2\sqrt{2x-4}\right)\left(x-2\sqrt{2x-4}\right)}=2x+2\sqrt{x^2-4\left(2x-4\right)}=2x+2\sqrt{x^2-8x+16}=2x+2\sqrt{\left(x-4\right)^2}=2x+2\left|x-4\right|\)

Suy ra A=$\sqrt{2x+2|x-4|}

Lời giải:

\(A\sqrt{2}=\sqrt{2x+4\sqrt{2x-4}}+\sqrt{2x-4\sqrt{2x-4}}\)

\(=\sqrt{(2x-4)+4\sqrt{2x-4}+4}+\sqrt{(2x-4)-4\sqrt{2x-4}+4}\)

\(=\sqrt{(\sqrt{2x-4}+2)^2}+\sqrt{(\sqrt{2x-4}-2)^2}\)

\(=|\sqrt{2x-4}+2|+|\sqrt{2x-4}-2|\)

Nếu $x\geq 4$ thì:

$A=\sqrt{2x-4}+2+\sqrt{2x-4}-2=2\sqrt{2x-4}$

Nếu $2\leq x<4$ thì:

$A=\sqrt{2x-4}+2+2-\sqrt{2x-4}=4$

Lấy 2 phương trình nhân vế theo vế được:

\(x^3y^3=\left(xy+4\right)\left(3xy-4\right)\)

Đặt \(xy=t\) thì được:

\(t^3=\left(t+4\right)\left(3t-4\right)\)

\(\left(t-4\right)\left(t^2+t-4\right)=0\)

Làm nốt

Ban ơi, điểm M không đóng góp gì cho bài toán nên mình không vẽ ra nhé. 

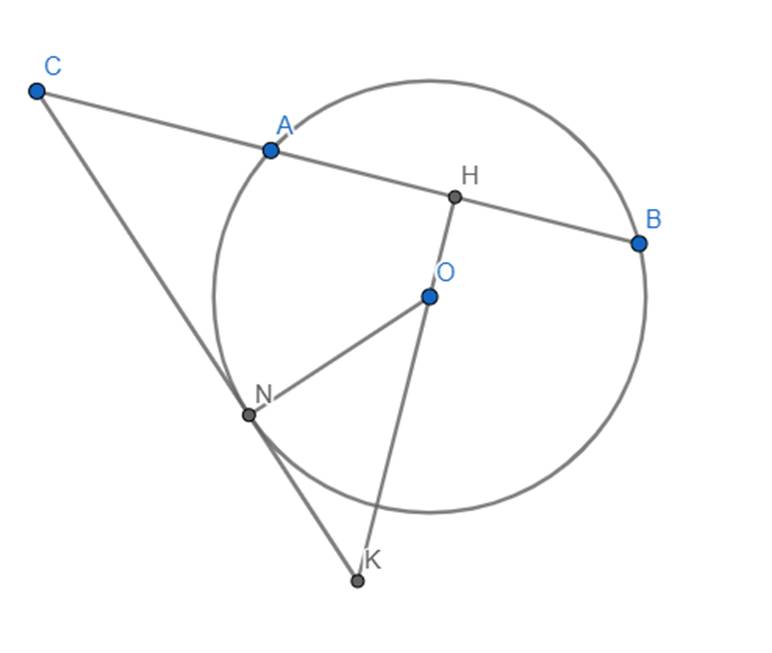
a) Xét (O) có H là trung điểm của dây AB, mà dây AB không đi qua O => OH vuông góc với (vgv) AB. => \(\widehat{OHC}=90^o\)

Vì CN là tiếp tuyến của (O) => CN vgv ON (tính chất tiếp tuyến)

=>  \(\widehat{ONC}=90^o\)

Xét tứ giác OHCN, ta có: 

\(\widehat{OHC}=90^o;\widehat{ONC}=90^o\Rightarrow\widehat{OHC}+\widehat{ONC}=180^o\) 

Mà chúng ở vị trí đối nhau

=> Tứ giác OHCN là tứ giác nội tiếp => O,H,C,N cùng thuộc 1 đường tròn.

b) Xét \(\Delta KNO\) và \(\Delta KHC\), ta có:

\(\widehat{HKN}\) chung

\(\widehat{KNO}=\widehat{KHC}=90^o\)

=> \(\Delta KNO\sim\Delta KHC\left(g.g\right)\)

=> \(\dfrac{KN}{KH}=\dfrac{KO}{KC}\)=> KN. KC = KH. KO

Hết rồi bạn nhé.

Câu này dùng bất: \(\sqrt{ab}\le\dfrac{a+b}{2}\)

Áp dụng bài toán được:

\(A=\dfrac{1}{\sqrt{1.1999}}+\dfrac{1}{\sqrt{2.1998}}+...\dfrac{1}{\sqrt{1999.1}}\)

\(>\dfrac{1}{\dfrac{1+1999}{2}}+\dfrac{1}{\dfrac{2+1998}{2}}+...+\dfrac{1}{\dfrac{1999+1}{2}}\)

\(=\dfrac{1}{1000}+\dfrac{1}{1000}+...+\dfrac{1}{1000}\)

Làm nốt

Ta có: \(\dfrac{1}{\left(k+1\right)\sqrt{k}}=\dfrac{\sqrt{k}}{k\left(k+1\right)}=\dfrac{\sqrt{k}}{k}-\dfrac{\sqrt{k}}{k+1}=\sqrt{k}\left(\dfrac{1}{\sqrt{k}}+\dfrac{1}{\sqrt{k+1}}\right)\left(\dfrac{1}{\sqrt{k}}-\dfrac{1}{\sqrt{k+1}}\right)\)

\(=\left(1+\dfrac{\sqrt{k}}{\sqrt{k+1}}\right)\left(\dfrac{1}{\sqrt{k}}-\dfrac{1}{\sqrt{k+1}}\right)< 2\left(\dfrac{1}{\sqrt{k}}-\dfrac{1}{\sqrt{k+1}}\right)\)

Suy ra\(\dfrac{1}{2\sqrt{1}}+\dfrac{1}{3\sqrt{2}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}}< 2\left(\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\right)\)

\(=2\left(\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{n+1}}\right)< 2\)

\(M_{ankan}=1,375.32=44\left(g\text{/}mol\right)\\ \rightarrow12n+2n+2=44\\ \Leftrightarrow n=3\left(TM\right)\)

Vậy CTPT của ankan là \(C_3H_8\)

CTCT: \(CH_3-CH_2-CH_3\)

\(M_{C_nH_{2n+2}}=M_{O_2}.1,375=32.1,375=44\left(đvC\right)\)

\(12n+2n+2=44\Leftrightarrow n=3\)

Vậy ankan là \(C_3H_6\).