\(1,2^3\cdot x^2=1,2^5\Leftrightarrow x^2=\dfrac{1,2^5}{1,2^3}=1,2^2=1,44\)

\(\Leftrightarrow x=1,2\) hoặc \(x=-1,2\)

Vậy x = 1,2 hoặc x = -1,2

(1,2)³.\(x^2\) = (1,2)⁵

         \(x^2\) = (1,2)⁵:(1,2)³

        \(x^2\) = (1,2)²

       \(\left[{}\begin{matrix}x=-1,2\\x=1,2\end{matrix}\right.\)

Các số tự nhiên nhỏ hơn `100` là : 

`1;2;3;4;...;99`

Khoảng cách : `1`

Số số hạng là :\(\dfrac{99-1}{1}+1=99\)

Tổng là : \(\dfrac{99+1\times99}{2}=4950\)

Ta có dãy các số tự nhiên nhỏ hơn 100: 0;1;2;3;...;99

Dãy có số số hạng là: (99-0):1+1=100 (số hạng)

Tổng của dãy là: (99+0)x100:2= 4950

Góc nhọn: \(\widehat{ABD};\widehat{ADB};\widehat{BEC};\widehat{EDC};\widehat{BDC};\widehat{ECD};\widehat{BCE};\widehat{BCD}\)

Góc vuông: \(\widehat{BAD}\)

Góc tù: \(\widehat{DBC};\widehat{EBC};\widehat{DEC}\)

a, Góc nhọn: \(\widehat{ABD}\);  \(\widehat{BCE}\); \(\widehat{BCD}\); \(\widehat{DCE}\); \(\widehat{BDC}\); \(\widehat{ADB}\); \(\widehat{BEC}\)

b, Góc vuông: \(\widehat{BAD}\); \(\widehat{ADC}\)

c, Góc tù: \(\widehat{ABC}\);  \(\widehat{CBD}\); \(\widehat{CED}\)

\(x\) \(\times\) \(\dfrac{14}{3}\) = 2,5

\(x\)           = 2,5 : \(\dfrac{14}{3}\) 

\(x\)           = \(\dfrac{15}{28}\)

x.14/3=2,5

x        =2,5:14/3

x        =15/28

Chúc bn hok tốt!!!

Trước hết ta phải chứng minh \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).

Thật vậy, \(\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{a+ab}{b^2+b}\) và \(\dfrac{a+1}{b+1}=\dfrac{\left(a+1\right)b}{\left(b+1\right)b}=\dfrac{ab+b}{b^2+b}\).

Mà theo giả thuyết là a < b nên \(\dfrac{a+ab}{b^2+b}< \dfrac{ab+b}{b^2+b}\), suy ra \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).

Từ đây ta có:

\(B=\dfrac{2022^{2022}+1}{2022^{2023}+1}=\dfrac{2022^{2023}+2022}{2022^{2024}+2022}=\dfrac{2022^{2023}+2021+1}{2022^{2024}+2021+1}\)

Đặt \(A_1=\dfrac{2022^{2023}+2}{2022^{2024}+2}=\dfrac{2022^{2023}+1+1}{2022^{2024}+1+1}\), rõ ràng \(A_1>A\).

Đặt \(A_2=\dfrac{2022^{2023}+3}{2022^{2024}+3}=\dfrac{2022^{2023}+2+1}{2022^{2024}+2+1}\), rõ ràng \(A_2>A_1\).

...

Đặt \(A_{2020}=\dfrac{2022^{2023}+2021}{2022^{2024}+2021}=\dfrac{2022^{2023}+2020+1}{2022^{2024}+2020+1}\), rõ ràng \(A_{2020}>A_{2019}\) và \(B>A_{2020}\).

Suy ra \(B>A_{2020}>A_{2019}>...>A_2>A_1>A\). Vậy A < B.

Ta có A = \(\dfrac{2022^{2023}}{2022^{2024}}=\dfrac{1}{2022}\) ; B = \(\dfrac{2022^{2022}}{2022^{2023}}=\dfrac{1}{2022}\)

Mà \(\dfrac{1}{2022}=\dfrac{1}{2022}\)

Vậy A = B

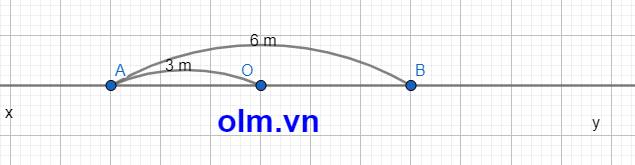
a, Các cặp tia đối nhau chung gốc A lần lượt là:

Ax và AO;  Ax và AB;  Ax và AY 

b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B

      ⇒ OA + OB = AB 

      ⇒ OB = AB - OA

         Độ dài đoạn OB là: 6 - 3 = 3 (cm)

  c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB 

`@` `\text {Ans}`

`\downarrow`

`xy100(z+1)`

`= (xy100)*z + xy100`

`= xyz100 + xy100`

Vì đa thức là tổng của những đơn thức bao gồm biến và hệ số

Vậy, biểu thức trên là đa thức.

không

a: Trên tia Ox, ta có: OM<ON

nên M nằm giữa O và N

=>OM+MN=ON

=>MN+4=8

=>MN=4(cm)

b: Ta có: M nằm giữa O và N

MN=MO(=4cm)

Do đó: M là trung điểm của ON

c: Trên tia Ox, ta có: OP<OM

nên P nằm giữa O và M

=>OP+PM=OM

=>PM+2=4

=>PM=2(cm)

Ta có: P nằm giữa O và M

mà OP=PM(=2cm)

nên P là trung điểm của OM

Trên tia Ox, ta có: OM<OQ

nên M nằm giữa O và Q

=>OM+MQ=OQ

=>MQ+4=6

=>MQ=2(cm)

Vì MP=MQ(=2cm)

nên M là trung điểm của PQ

Trên tia Ox, ta có: OQ<ON

nên Q nằm giữa O và N

=>OQ+QN=ON

=>QN+6=8

=>QN=2(cm)

Vì MQ=QN(=2cm)

nên Q là trung điểm của MN