Cho tam giác ABC, góc A bằng 90 độ, AB < AC lấy D thuộc BC, BD = BA, kẻ BI là phân giác của góc ABC
a) Chứng minh ID = IA
b) chứng minh BI là trung trực của Ad
c) Chứng minh ID vuông góc với BC
d) Trên tia đối Ai lấy điểm M, AM=AI Chứng minh BA là phân giác của góc MBI
e) Chứng minh BM=BI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thu gọn và sắp xếp đa thức
- \(x\) + 0,25\(\times\) 4 - 2\(x^3\) - 0,5\(x^2\)
= - \(x\) + 1 - 2\(x^3\) - 0,5\(x^2\)
= -2\(x^3\) - 0,5\(x^2\) - \(x\) + 1

\(F\left(x\right)=2x^3-7x^2+12x+a\)
\(G\left(x\right)=x+2\)
\(F\left(x\right):G\left(x\right)=2x^2-11x+34\) dư \(a-68\)
Để \(F\left(x\right)⋮G\left(x\right)\Rightarrow a-68=0\Rightarrow a=68\)


\(A=\dfrac{2.2^{12}.3^8+2^2.2^9.3^9}{2^7\left(2^7.3^7+2^3.5.3^8\right)}=\dfrac{2^{13}.3^8+2^{11}.3^9}{2^7\left(2^7.3^7+2^3.5.3^8\right)}\)
\(A=\dfrac{2^{11}.3^8\left(2^2+3\right)}{2^7.2^3.3^7\left(2^4+5.3\right)}\)
\(A=\dfrac{2.3.7}{31}=\dfrac{42}{31}\)

Số tấn gạo xuất kho lần 1 :
\(125.\dfrac{1}{5}=25\) (tấn)
Số tấn gạo xuất kho lần 2 :
\(125.\dfrac{25}{100}=31,25\) (tấn)
Số tân gạo nhập kho lần 3 :
\(11\dfrac{3}{4}=11,75\) (tấn)
Số tấn gạo có trong kho lúc này là :
\(125-25-31,25+11,75=80,5\) (tấn)

`@` `\text {Ans}`
`\downarrow`
`a)`
\(-5(x^2 - 3x +1 ) + x ( 1+5x ) =x-2 \)
`=> -5x^2 + 15x - 5 + x + 5x^2 = x - 2`
`=> (-5x^2 + 5x^2) + (15x + x) - 5 = x - 2`
`=> 16x - 5 = x - 2`
`=> 16x - 5 - x + 2 = 0`
`=> (16x - x) + (-5+2) = 0`
`=> 15x - 3 = 0`
`=> 15x = 3`
`=> x = 3 \div 15`
`=> x =`\(\dfrac{1}{5}\)
Vậy, `x =`\(\dfrac{1}{5}\)
`b)`
\(-4x (x-5) +7x (x-4) -3x^2 =12\)
`=> -4x^2 + 20x + 7x^2 - 28x - 3x^2 = 12`
`=> (-4x^2 - 3x^2 + 7x^2) + (20x - 28x) = 12`
`=> -8x = 12`
`=> x = 12 \div (-8)`
`=> x = `\(-\dfrac{3}{2}\)
Vậy, `x =`\(-\dfrac{3}{2}\)
`@` `\text {Kaizuu lv uu}`

a) \(A=\left(-0,75-\dfrac{1}{4}\right):\left(-5\right)+\dfrac{1}{48}-\left(-\dfrac{1}{6}\right):\left(-3\right)\)
\(A=\left(-0,75-0,25\right):\left(-5\right)+\dfrac{1}{48}-\left(-\dfrac{1}{6}\right)\cdot\dfrac{-1}{3}\)
\(A=\left(-1\right):\left(-5\right)+\dfrac{1}{48}-\dfrac{1}{18}\)
\(A=\dfrac{1}{5}+\dfrac{1}{48}-\dfrac{1}{18}\)
\(A=\dfrac{119}{720}\)
b) \(B=\left(\dfrac{6}{25}-1,24\right):\dfrac{3}{7}:\left[\left(3\dfrac{1}{2}-3\dfrac{2}{3}\right):\dfrac{1}{14}\right]\)
\(B=\left(0,24-1,24\right):\dfrac{3}{7}:\left[\left(\dfrac{7}{2}-\dfrac{11}{3}\right):\dfrac{1}{14}\right]\)
\(B=-1:\dfrac{3}{7}:\left(-\dfrac{1}{6}:\dfrac{1}{14}\right)\)
\(B=-\dfrac{7}{3}:-\dfrac{7}{3}\)
\(B=1\)
a, A = (-0,75 - \(\dfrac{1}{4}\)) : (-5) + \(\dfrac{1}{48}\) - (- \(\dfrac{1}{6}\)) : (-3)
A = -(0,75 + 0,25): (-5) + \(\dfrac{1}{48}\) - \(\dfrac{1}{18}\)
A = -1 : (-5) + \(\dfrac{1}{48}\) - \(\dfrac{1}{18}\)
A = \(\dfrac{1}{5}\) + \(\dfrac{1}{48}\) - \(\dfrac{1}{18}\)
A = \(\dfrac{53}{240}\) - \(\dfrac{1}{18}\)
A = \(\dfrac{119}{720}\)
b, B = (\(\dfrac{6}{25}\) - 1,24): \(\dfrac{3}{7}\): [(3\(\dfrac{1}{2}\) - 3\(\dfrac{2}{3}\)): \(\dfrac{1}{14}\)]
B = (0,24 - 1,24): \(\dfrac{3}{7}\):[(\(\dfrac{7}{2}\)-\(\dfrac{11}{3}\)): \(\dfrac{1}{14}\)]
B = -1: \(\dfrac{3}{7}\):[ (-\(\dfrac{1}{6}\) : \(\dfrac{1}{14}\))]
B = -1: \(\dfrac{3}{7}\): (- \(\dfrac{7}{3}\))
B = 1 \(\times\) \(\dfrac{7}{3}\) \(\times\) \(\dfrac{3}{7}\)
B = 1

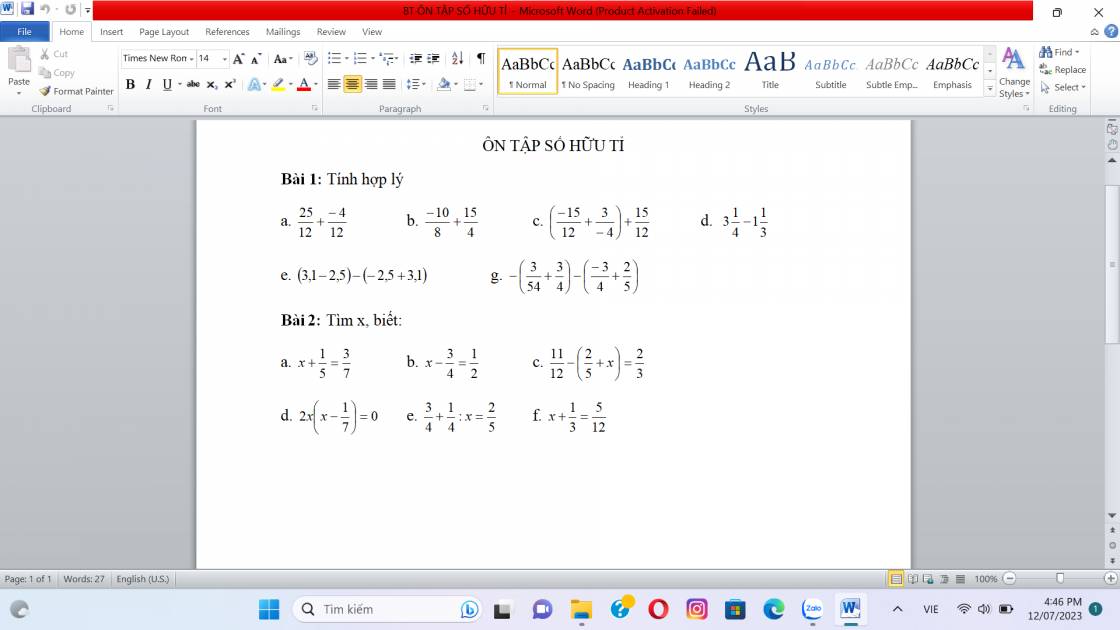
Bài 1:
a. $=\frac{25-4}{12}=\frac{21}{12}=\frac{7}{4}$
b. $=\frac{-5}{4}+\frac{15}{4}=\frac{15-5}{4}=\frac{10}{4}=\frac{5}{2}$
c. $=\frac{-15}{12}+\frac{15}{12}+\frac{3}{-4}=\frac{-15+15}{12}+\frac{3}{-4}=\frac{3}{-4}$
d.
$=3+\frac{1}{4}-1-\frac{1}{3}=(3-1)-(\frac{1}{3}-\frac{1}{4})$
$=2-\frac{1}{12}=\frac{23}{12}$
e.
$=3,1-2,5+2,5-3,1=(3,1-3,1)-(2,5-2,5)=0-0=0$
g.
$=\frac{1}{18}-\frac{3}{4}+\frac{3}{4}-\frac{2}{5}$
$=\frac{1}{18}-\frac{2}{5}=\frac{-31}{90}$
Bài 2:
a.
$x+\frac{1}{5}=\frac{3}{7}$
$x=\frac{3}{7}-\frac{1}{5}=\frac{8}{35}$
b.
$x=\frac{1}{2}+\frac{3}{4}=\frac{2}{4}+\frac{3}{4}=\frac{5}{4}$
c.
$\frac{2}{5}+x=\frac{11}{12}-\frac{2}{3}=\frac{1}{4}$
$x=\frac{1}{4}-\frac{2}{5}=\frac{-3}{20}$
d.
$2x(x-\frac{1}{7})=0$
$\Rightarrow 2x=0$ hoặc $x-\frac{1}{7}=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{7}$
e.
$\frac{1}{4}:x=\frac{2}{5}-\frac{3}{4}=\frac{-7}{20}$
$x=\frac{1}{4}: \frac{-7}{20}=\frac{-5}{7}$
f.
$x=\frac{5}{12}-\frac{1}{3}=\frac{1}{12}$
a) Xét Δ ABI và Δ BDI ta có :
BD=BA (đề bài)
Góc ABI = Góc IBD (BI là phân giác góc ABC)
BI là cạnh chung
⇒ Δ ABI = Δ BDI (cạnh, góc, cạnh)
⇒ IA=ID
b) Gọi E là giao điểm của BI và AD
Ta có : BD=BA
⇒ Δ ABD là Δ cân tại B
mà BE là đường phân giác (BI là phân giác và B,E,I thẳng hàng)
⇒ BE là đường cao Δ ABD
⇒ BE \(\perp\) AD
⇒ BI \(\perp\) AD
mà BD=BA (đề bài) và ID=IA (cmt)
⇒ BI là đường trung trực của AD
c) vì Δ ABI = Δ BDI
mà A=90o , Góc ABI = Góc IBD
⇒ Góc BDI = 90o
⇒ ID \(\perp\) BC
d) Xét Δ ABI và Δ BAM ta có :
AM=AI (đề bài)
Góc BAI = Góc BAM =90o (do M,A,I thẳng hàng)
AB là cạnh chung
⇒ Δ ABI = Δ BAM (cạnh, góc, cạnh)
⇒ Góc ABI= Góc ABM
⇒ AB là phân giác góc MBI
e) BM=BI (Δ ABI = Δ BAM)