: Cho hai số biết số bé là 7856, số này kém trung bình cộng của hai số là 344 đơn vị. Tìm số lớn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số lớn nhất có 3 chữ số là 999
Số lớn nhát có hai chữ số là 99
Tổng của hai số là: 999x2 = 1998
Số cần tìm là : 1998-99 = 1899
đ/s: 1899
Vì trung bình cộng của 2 số là số lớn nhất có 3 chữ số nên trung bình của 2 số đó là : 999
Tổng của 2 số đó là :
999 x 2 = 1998
vì một số là số lớn nhất có 2 chữ số là : 99
Số còn lại là :
1998 - 99 = 1899
Đ/s...

Lời giải:
Khi đặt số trừ thẳng với chữ số hàng trăm, nghĩa là ta đã trừ số bị trừ cho 1 số mới gấp 100 lần số trừ cũ.
99 lần số trừ cũ là: $783-486 = 297$
Số trừ cũ: $297:99=3$
Số bị trừ: $3+783=786$

gọi số đó là abcd
Ta thấy:
a có 4 cách chọn
b có 3 cách chọn(vì a đã chọn 1 chữ số )
c có 2 cách chọn
d có 1 cách chọn
Vậy có tất cả 1x2x3x4=24 cách chọn số
Đ/s:24 cách chọn

Số lớn nhất có 1 chữ số là : \(9\)
Số nhỏ nhất có 3 chữ số là : \(100\)
Hiệu của 2 số đó là :
\(9x100=900\)
Số lớn là :
\(\left(4672+900\right):2=2786\)
Số bé là :
\(4672-2786=1886\)
Đáp số...

x + x : 1/5 + x : 1/8 - x × 4 = 1250
x + x × 5 + x × 8 - 4 × x = 1250
x × (1 + 5 + 8 - 4) = 1250
x × 10 = 1250
x = 1250 : 10
x = 125

a) 45; 48; 51; 54 là các số chia hết cho 3
15 chia hết cho 3 nên 15 thuộc dãy số đã cho
124 không chia hết cho 3 nên không thuộc dãy số đã cho
b) Ta có:
3 × 2 = 6
6 × 2 = 12
12 × 2 = 24
Chữ số tận cùng của các số tiếp theo chỉ có thể là 2; 4; 6; 8
Vậy 1000; 729; 1110 không thuộc dãy số đã cho

Gọi số cần tìm là:a
Theo bài ra:a chia cho 2;3;4;5;7 đều dư 1 nên a-1 chia hết cho 2;3;4;5;7
Mà a nhỏ nhất nên a-1 nhỏ nhất
Số nhỏ nhất chia hết cho 2,3,4,5,7 là:420
Suy ra:a-1=420
a=421
Vậy số cần tìm là:421
C2:
Gọi số cần tìm là X
X : 2 ; 3 ; 4 ; 5 ; 7 đều dư 1 nên X - 1 sẽ chia hết cho 2 ; 3 ; 4 ; 5 ; 7
Vì số chia hết cho 4 sẽ chia hết cho 2, => X - 1 = 3 x 4 x 5 x 7 = 420
Vậy X = 420 + 1 = 421

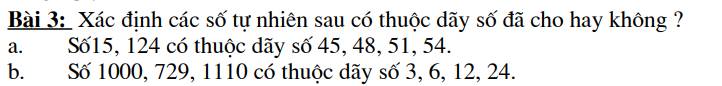
trung bình cộng hai số =7856+344=8200
tổng hai số =8200*2=16400
số lớn =16400-7856=8544