Bài 1:

a) \(A=\left\{x=2k+1|k\in N,0\le k\le6\right\}\) 

\(B=\left\{x\in N|0\le x\le8\right\}\) 

b) C là giao của tập hợp A và B 

\(\Rightarrow C=\left\{1;3;5;7\right\}\)

\(\Rightarrow C=\left\{x=2k+1|k\in N,0\le k\le3\right\}\)

c) D là hợp của tập hơn A và B 

\(\Rightarrow D=\left\{0;1;2;3;4;5;6;7;8;9;11;13\right\}\) 

d) Các phát biểu đúng là:

\(E\subset B,E\subset D\)

hỗn số là số được viết dưới dạng \(x\dfrac{a}{b}\)trong đó x là một số nguyên còn \(\dfrac{a}{b}\) là một số thập phân nhỏ hơn 1

- Hỗn số là sự biểu diễn ngắn gọn về tổng của một số tự nhiên với một phân số nhỏ hơn 1.

Thuế VAT mà bác Minh phải trả khi mua chiếc điện thoại là:

\(10\%\cdot7990000=799000\left(đ\right)\) 

Số tiền mà bác Minh phải trả khi mua chiếc điện thoại là:

\(7990000+799000=8789000\left(đ\right)\) 

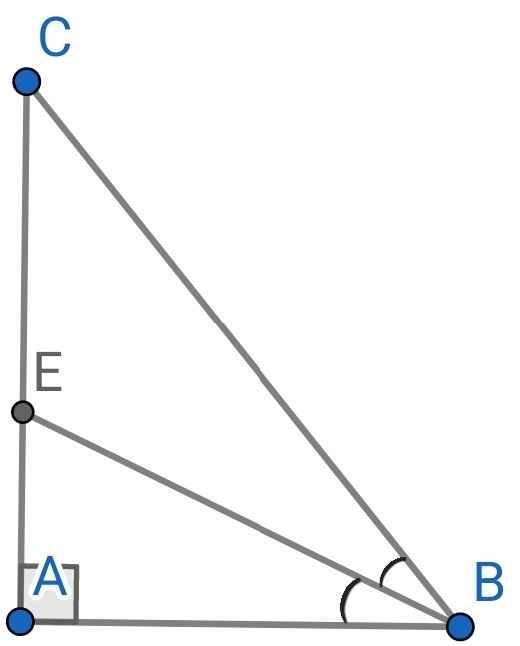   ∆ABC có BE là đường phân giác (gt)

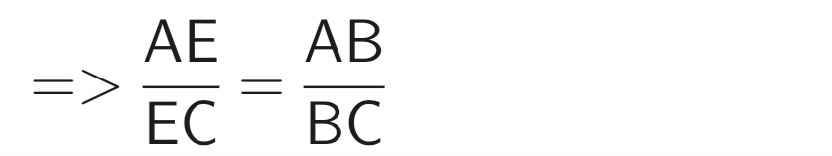
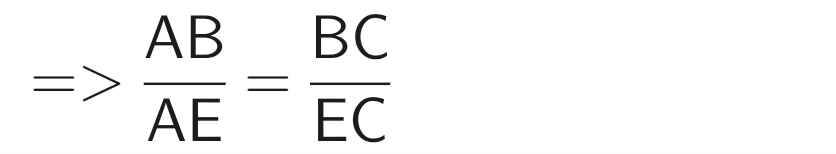
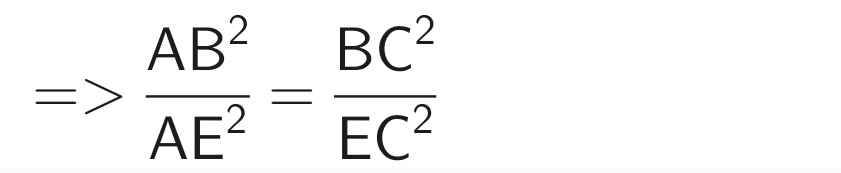  ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

⇒ BC² - AB² = AC²

= (3 + 5)²

= 64

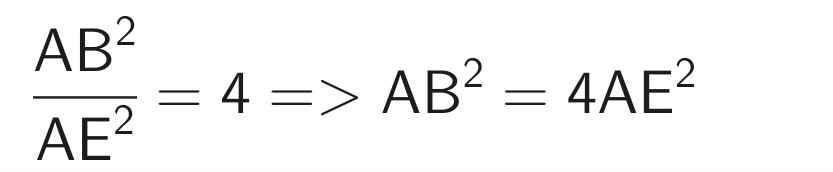
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

  Ta có:

BC² = AB² + AC² (Pythagore)

= 6² + 64

= 100

⇒ BC = 10

vì BE là đường phân giác của tam giác ABC nên ta có:

\(\dfrac{AE}{EC}=\dfrac{AB}{BC}=\dfrac{3}{5}\)

\(BC=\dfrac{5}{3}AB\)

áp dụng định lý pythagore vào tam giác ABC ta được:

\(AC^2=AB^2+BC^2\)

tổng độ dài đoạn AC là: 3 + 5 = 8

\(AB^2+BC^2=8^2\\ AB^2+\left(\dfrac{5}{3}AB\right)^2=64\\ AB^2+\dfrac{25}{9}AB^2=64\\ AB^2\cdot\left(1+\dfrac{25}{9}\right)=64\\ AB^2\cdot\dfrac{34}{9}=64\\ AB^2=64:\dfrac{34}{9}=64\cdot\dfrac{9}{34}\\ AB^2=\dfrac{576}{34}\\ AB=\sqrt{\dfrac{576}{34}}\text{≈}4,11\)

độ dài đoạn BC là:

BC² = AC² - AB²

BC² = 64 - 16,8921

BC² = 47,1079

BC = \(\sqrt{47,1079}\) ≈ 6,86

VẬY AB = 4,11; BC  =6,86

\(\left[{}\begin{matrix}2x+3=x-5\\2x+3=5-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\3x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\)

cái này trong đề ôn thi của mình lên thcs á

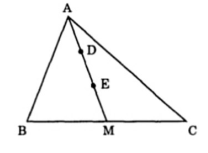
a: Vì MB=MC

nên M là trung điểm của BC

=>\(S_{EBM}=S_{EMC}=\dfrac{S_{BEC}}{2}=210\left(cm^2\right)\)

Vì AD=DE=EM

nên \(AE=\dfrac{2}{3}AM\)

Xét ΔABC có

AM là đường trung tuyến

\(AE=\dfrac{2}{3}AM\)

Do đó: E là trọng tâm của ΔABC

Các tam giác có chung đỉnh A là ΔABD,ΔABE,ΔABM;ΔACD;ΔACE;ΔACM;ΔABC

Vì AD=DE=EM

và AD+DE+EM=AM

nên \(AD=DE=EM=\dfrac{1}{3}AM\)

=>\(S_{ABD}=S_{BDE}=S_{EBM}=210\left(cm^2\right)\)

\(S_{ABE}=S_{ABD}+S_{BDE}=420\left(cm^2\right)\)

\(S_{ABM}=S_{ABD}+S_{BDE}+S_{EBM}=630\left(cm^2\right)\)

Vì AD=DE=EM

nên \(S_{ACD}=S_{DCE}=S_{EMC}=210\left(cm^2\right)\)

\(S_{AEC}=S_{ADC}+S_{DEC}=420\left(cm^2\right)\)

\(S_{AMC}=S_{ADC}+S_{DEC}+S_{EMC}=630\left(cm^2\right)\)

\(S_{ABC}=S_{AMB}+S_{AMC}=1260\left(cm^2\right)\)

b: Xét ΔABC có

E là trọng tâm

BE cắt AC tại N

Do đó: N là trung điểm của AC(ĐPCM)

Đa thức $2x^4-21x^2+1$ không phân tích thành nhân tử bạn nhé.

Đặt \(f\left(x\right)=y=\dfrac{1}{3}x^3-\left(2m-1\right)x^2+\left(m^2-m+7\right)x+m-5\)

=>\(y'=\dfrac{1}{3}\cdot3x^2-\left(2m-1\right)\cdot2x^2+\left(m^2-m+7\right)\)

=>\(y'=x^2-\left(4m-2\right)x^2+\left(m^2-m+7\right)\)

Đặt y'=0

\(\text{Δ}=\left(4m-2\right)^2-4\left(m^2-m+7\right)\)

\(=16m^2-16m+4-4m^2+4m-28=12m^2-12m-24\)

Để hàm số f(x) có hai cực trị thì Δ>0

=>\(12\left(m^2-m-2\right)>0\)

=>\(m^2-m-2>0\)

=>(m-2)(m+1)>0

=>\(\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4m-2\\x_1x_2=\dfrac{c}{a}=m^2-m+7\end{matrix}\right.\)

\(x_1^2+x_2^2=\left(\sqrt{74}\right)^2=74\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2=74\)

=>\(\left(4m-2\right)^2-2\left(m^2-m+7\right)=74\)

=>\(16m^2-16m+4-2m^2+2m-14=74\)

=>\(14m^2-14m-84=0\)

=>\(m^2-m-6=0\)

=>(m-3)(m+2)=0

=>\(\left[{}\begin{matrix}m=3\left(nhận\right)\\m=-2\left(nhận\right)\end{matrix}\right.\)

hi

$20+(4^2-4)-2$

$=(20-2)+(16-4)$

$=18+12=30$

30