1 + 1 = 3 Vì sao? ( Gợi ý: lí thuyết vật lý của Albert Einstein )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(I\) là tâm tỉ cự của 3 điểm A, B, C ứng với bộ \(\left(1,4,1\right)\).
Khi đó: \(\overrightarrow{IA}+4\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\). Gọi Y là trung điểm AC thì \(4\overrightarrow{IB}+2\overrightarrow{IY}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{IY}=-2\overrightarrow{IB}\)
Từ đó dễ dàng xác định được vị trí của I là điểm nằm trên cạnh BY sao cho \(IY=2IB\)
Gọi \(J\) là tâm tỉ cự của 3 điểm A, B, C ứng với bộ \(\left(9,-6,3\right)\). Khi đó \(9\overrightarrow{JA}-6\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\)
\(\Leftrightarrow3\left(\overrightarrow{JA}+\overrightarrow{JC}\right)+6\left(\overrightarrow{JA}-\overrightarrow{JB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow6\overrightarrow{JY}+6\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{JY}=\overrightarrow{AB}\)
Vậy ta thấy J là điểm sao cho tứ giác ABYJ là hình hình hành.

Ta có \(\left|\overrightarrow{MA}+4\overrightarrow{MB}+\overrightarrow{MC}\right|+3\left|3\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{MI}+\overrightarrow{IA}+4\left(\overrightarrow{MI}+\overrightarrow{IB}\right)+\overrightarrow{MI}+\overrightarrow{IC}\right|+\left|9\left(\overrightarrow{MJ}+\overrightarrow{JA}\right)-6\left(\overrightarrow{MJ}+\overrightarrow{JB}\right)+3\left(\overrightarrow{MJ}+\overrightarrow{JC}\right)\right|\)
\(=\left|6\overrightarrow{MI}\right|+\left|6\overrightarrow{MJ}\right|\)
\(=6\left(MI+MJ\right)\)
Vậy ta cần tìm M để \(MI+MJ\) đạt GTNN. Ta thấy \(MI+MJ\ge IJ=const\). Dấu "=" xảy ra \(\Leftrightarrow\) M nằm trên đoạn thẳng IJ.

Đây là dạng toán tổng hiệu ẩn tổng em nhé. Cấu trúc đề thi chuyên, thi học sinh giỏi, thi violympic.
Hôm nay olm sẽ hướng dẫn em giải dạng này như sau.
Bước 1: tìm tổng đang bị ẩn
Bươc 2: giải theo toán tổng hiệu
Phân tích đề vì số thứ nhất cộng với số thứ hai sẽ được tổng, rồi lại lấy tổng đó cộng với tổng sẽ được 2010 vậy 2010 gấp 2 lần tổng. từ đó tìm được tổng, biêt tổng và hiệu rồi giải như toán tổng hiệu thông thường.
Giải:
Tổng hai số là: 2010 : 2 = 1005
Ta có sơ đồ:
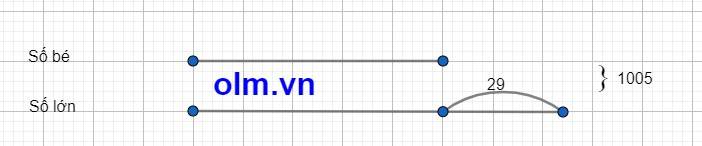
Theo sơ đồ ta có:
Số lớn là: (1005 + 29) : 2 = 571
Số bé là: 1005 - 571 = 434
Đáp số: ..............

Vì hình chữ nhật đó được chia thành 4 hình chữ nhật nhỏ như hình vẽ nên tỉ số chiều rộng và chiều dài là:
1 : 4 = \(\dfrac{1}{4}\)
Nửa chu vi của hình chữ nhật là: 56 : 2 = 28 (cm)
Ta có sơ đồ:
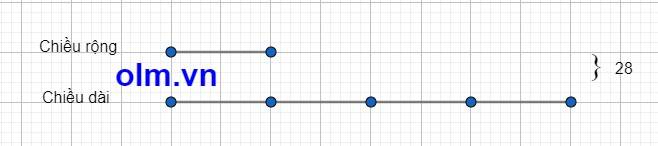
Chiều rộng hình chữ nhật là:
28 : (1 + 4) = 5,6 (cm)
Chiều dài hình chữ nhật là:
28 - 5,6 = 22,4 (cm)
Diện tích hình chữ nhật là:
22,4 x 5,6 = 125,44 (cm2)
Diện tích mỗi hình chữ nhật nhỏ là:
125,44 : 4 = 31,36 (cm2)
Đáp số: 31,36 cm2

Vậy ta thấy, nếu cửa hàng làm 66 phần bánh loại A và 22 phần bánh loại B thì sẽ đạt được lợi nhuận cao nhất.
Gọi �x, y$ lần lượt là số phần bánh loại A và loại B mà cửa hàng làm ra.
Theo đề bài, ta thấy
Để làm ra �x phần bánh loại A cần 2�2x gam bột, �x gam đường và 5�5x gam nhân bánh;
Để làm ra �y phần bánh loại B cần �y gam bột, 2�2y gam đường và 5�5y gam nhân bánh.
Lợi nhuận của cửa hàng là �(�)=16�+20�F(x)=16x+20y ( nghìn đồng).
Theo đề bài, ta có hệ bất phương trình { 2�+�≤20 �+2�≤105�+5�≤40 �,�∈�⎩⎨⎧ 2x+y≤20x+2y≤105x+5y≤40x,y∈N
Biểu diễn lên hệ trục ���Oxy, ta có miền nghiệm là tứ giác ����OABC, kể cả các cạnh của tứ giác (như hình vẽ) với �(0;0)O(0;0), �(0;5),A(0;5), �(6;2),B(6;2), �(8;0)C(8;0).
Ta tính lợi nhuận của cửa hàng tại tọa độ các đỉnh của miền nghiệm:
�(0;0)=0F(0;0)=0 nghìn đồng; �(0;5)=100F(0;5)=100 nghìn đồng
�(6;2)=136F(6;2)=136 nghìn đồng; �(8;0)=128F(8;0)=128 nghìn đồng
Vậy ta thấy, nếu cửa hàng làm 66 phần bánh loại A và 22 phần bánh loại B thì sẽ đạt được lợi nhuận cao nhất.

Để A ∩ B có đúng 4 phần tử nguyên thì:
m - 1 < -1; m + 5 ≥ 2 và m ∈ Z
*) m - 1 < -1
m < 0
*) m + 5 ≥ 2
m ≥ 2 - 5
m ≥ -3
Vậy -3 ≤ m < 0 và m ∈ Z thì A ∩ B có đúng 4 phần tử nguyên
đoạn A=[-1;2] có 4 phần tử nguyên là {-1;0;1;2}
Với �∈�m∈Z, �=(�−1;�+5]B=(m−1;m+5] có các phần tử nguyên là: {�;�+1;�+2;�+3;�+4;�+5}{m;m+1;m+2;m+3;m+4;m+5}.
Để �∩�A∩B có đúng 44 phần tử nguyên thì [�=−1�+1=−1�+2=−1⇔[�=−1�=−2�=−3m=−1m+1=−1m+2=−1⇔m=−1m=−2m=−3.
Vậy có 33 giá trị nguyên của �m thỏa mãn đề bài.

a) Liệt kê các phần tử của tập hợp �={�∈�∣ 2�2+3�+1=0 }A={x∈Z 2x2+3x+1=0 }
Ta có: 2�2+3�+1=0⇔[ �=−12 �=−1 2x2+3x+1=0⇔ x=−21 x=−1 .
Do đó: �={−1}A={−1}.
b) Cho hai tập hợp �={�∈�∣∣�∣>4}A={x∈R∣x∣>4} và �={�∈�∣−5≤�−1<5}B={x∈R−5≤x−1<5}. Xác định tập �=�\�X=B\A.
Ta có:
⚡∣�∣>4⇔[ �>4 �<−4⇒�=(−∞;−4)∪(4;+∞ )∣x∣>4⇔[ x>4x<−4⇒A=(−∞;−4)∪(4;+∞ ).
⚡−5≤�−1<5⇔−4≤�<6⇒�=[−4;6)−5≤x−1<5⇔−4≤x<6⇒B=[−4;6).
Suy ra �=�\�=[−4;4]X=B\A=[−4;4].

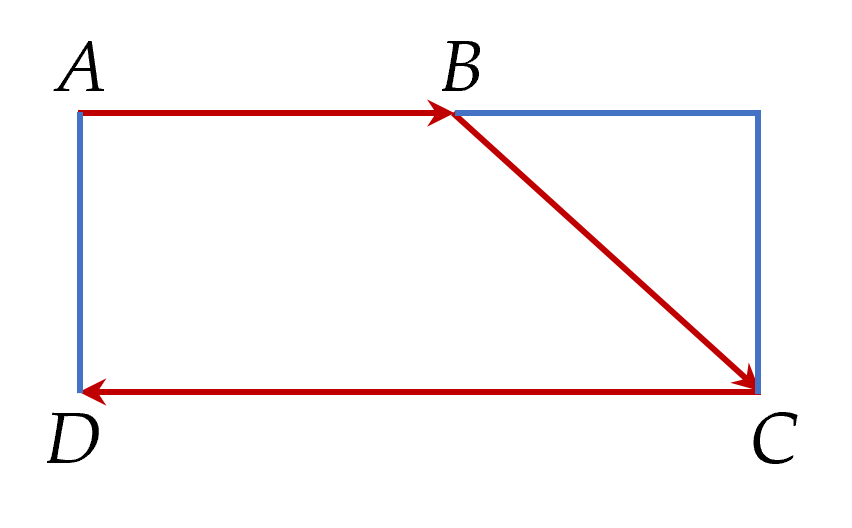






Vì bạn tính sai?