3x=4y=-2z và 2x-3y+4z=75 tìm x,y,z thỏa mãn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, cảm ơn em đã phản hồi đến Olm. Vấn đề em hỏi Olm xin giải đáp như sau:
Em khẳng định mặt trời mọc ở đằng đông, đây cũng là chân lí, là thực tế không thể thay đổi trong bất cứ thời đại nào. Nên việc ngày mai ,mặt trời mọc ở đằng tây là không thể xảy ra.
Vậy biến cố: Ngày mai, mặt trời mọc ở đằng tây là biến cố không thể em nhé!

Bạn bấm vào biểu tượng ![]() để nhập các công thức toán học cho rõ ràng nhé!
để nhập các công thức toán học cho rõ ràng nhé!
Vd:\(3^{10}\)

\(\dfrac{x-2y}{z-y}=-5\Rightarrow\dfrac{x-2y}{y-z}=5\\ \Rightarrow x-2y=5\left(y-z\right)\\ \Rightarrow x-2y=5y-5z\\ \Rightarrow x+5z=7y\)
Ta có:
\(\dfrac{1}{7}\cdot\dfrac{x-2z}{y-z}=\dfrac{x-2z}{7\left(y-z\right)}=\dfrac{x-2z}{7y-7z}\\ =\dfrac{x-2z}{x+5z-7z}=\dfrac{x-2z}{x-2z}=1\)
\(\Rightarrow\dfrac{x-2z}{y-z}=1:\dfrac{1}{7}=7\)

\(\left(\dfrac{2}{7}-\dfrac{9}{4}\right)-\left(-\dfrac{3}{7}+\dfrac{5}{4}\right)-\left(\dfrac{2}{4}-\dfrac{9}{7}\right)\)
\(=\dfrac{2}{7}-\dfrac{9}{4}+\dfrac{3}{7}-\dfrac{5}{4}-\dfrac{2}{4}+\dfrac{9}{7}\)
\(=\left(\dfrac{2}{7}+\dfrac{3}{7}+\dfrac{9}{7}\right)-\left(\dfrac{9}{4}+\dfrac{5}{4}+\dfrac{2}{4}\right)\)
\(=2-4\)
\(=-2\)

\(\left(\dfrac{1}{2}-\dfrac{1}{3}\right)-\left(\dfrac{5}{3}-\dfrac{3}{2}\right)+\left(\dfrac{7}{3}-\dfrac{5}{2}\right)\\ =\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{5}{3}+\dfrac{3}{2}+\dfrac{7}{3}-\dfrac{5}{2}\\ =\left(\dfrac{1}{2}+\dfrac{3}{2}-\dfrac{5}{2}\right)+\left(-\dfrac{1}{3}-\dfrac{5}{3}+\dfrac{7}{3}\right)\\ =-\dfrac{1}{2}+\dfrac{1}{3}\\ =-\dfrac{1}{6}\)

\(a)4^7:2^5\\ =\left(2^2\right)^7:2^5\\ =2^{14}:2^5\\ =2^9\\ b)3^{10}:9^3\\ =3^{10}:\left(3^2\right)^3\\ =3^{10}:3^6\\ =3^4\\ c)27^9:3^{10}\\ \left(3^3\right)^9:3^{10}\\ =3^{27}:3^{10}\\ =3^{17}\\ d)25^5:5^3\\ =\left(5^2\right)^5:5^3\\ =5^{10}:5^3\\ =5^7\\ e)36^7:6^4\\ =\left(6^2\right)^7:6^4\\ =6^{14}:6^4\\ =6^{10}\\ g)4^3\cdot8^4\\ =\left(2^2\right)^3\cdot\left(2^3\right)^4\\ =2^6\cdot3^{12}\\ =2^{18}\)


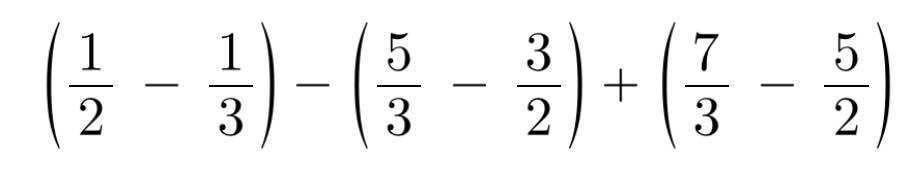
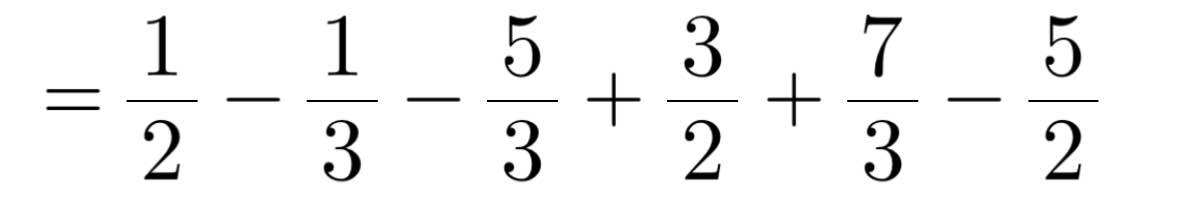
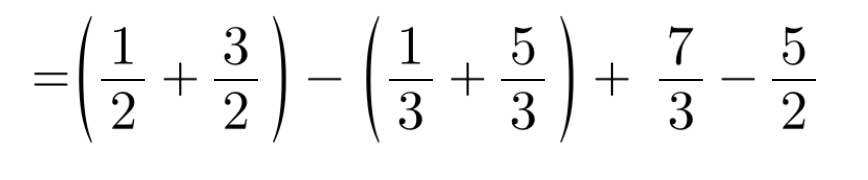
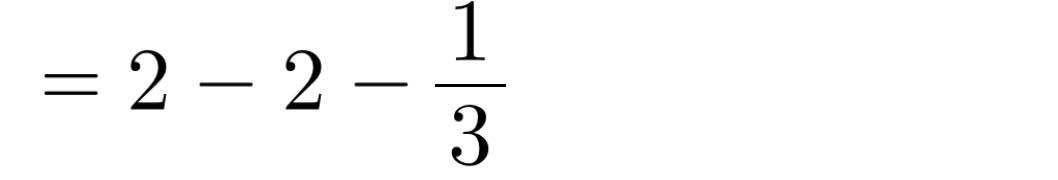

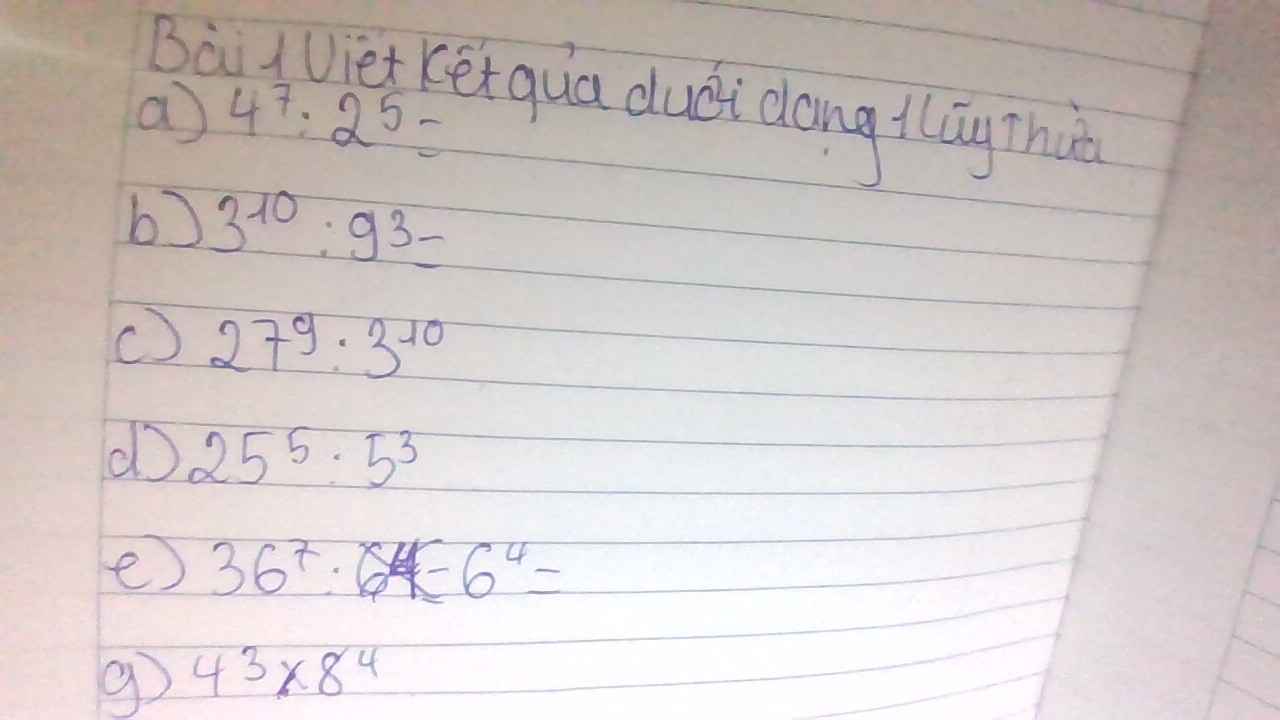
Theo đề bài ta có :
\(3x=4y=-2z\)
\(\Rightarrow\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=-\dfrac{z}{\dfrac{1}{2}}\)
mà \(2x-3y+4z=75\)
\(\Rightarrow\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=-\dfrac{z}{\dfrac{1}{2}}=\dfrac{2x-3y+4z}{\dfrac{2}{3}-\dfrac{3}{4}-2}=\dfrac{75}{-\dfrac{25}{12}}=-36\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{3}}=36\\\dfrac{y}{\dfrac{1}{4}}=36\\-\dfrac{z}{\dfrac{1}{2}}=36\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=12\\y=9\\z=-18\end{matrix}\right.\)
Vậy \(\left(x;y;z\right)=\left(12;9;-18\right)\)
Đặt \(t=3x=4y=-2z\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{t}{3}\\y=\dfrac{t}{4}\\z=-\dfrac{t}{2}\end{matrix}\right.\)
Thay vào phương trình còn lại. Chúng ta được
\(\dfrac{2}{3}t+\dfrac{3}{4}t-\dfrac{4}{2}t=75\)
\(\Leftrightarrow-\dfrac{7}{12}t=75\)
\(\Leftrightarrow t=-\dfrac{900}{7}\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{300}{7}\\y=-\dfrac{225}{7}\\z=\dfrac{450}{7}\end{matrix}\right.\)