tinh ti so phan tram (lam tron den hang phan muoi)cua 5ta so voi 7 ta
b) tim 1 so biet 20 phan tram cua no la 420Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


15/(-x) = -3/4
-x.(-3) = 15.4
3x = 60
x = 60 : 3
x = 20
y/8 = -3/4
4y = 8.(-3)
4y = -24
y = -24 : 4
y = -6

\(\dfrac{x-2}{3}=\dfrac{x+1}{4}\)
=>4(x-2)=3(x+1)
=>4x-8=3x+3
=>x=11

\(x+\dfrac{1}{3}=\dfrac{25}{-5}\)
\(x+\dfrac{1}{3}=-5\)
\(x=-5-\dfrac{1}{3}\)
\(x=-\dfrac{16}{3}\)

\(\dfrac{7}{8}+x=\dfrac{7}{20}\)
=>\(x=\dfrac{7}{20}-\dfrac{7}{8}=\dfrac{14}{40}-\dfrac{35}{40}=-\dfrac{21}{40}\)

\(\left(-1,5\right)\cdot\dfrac{-2}{3}+\left(2,5-\dfrac{3}{4}\right):1\dfrac{3}{4}\)
\(=\dfrac{-3}{2}\cdot\dfrac{-2}{3}+\left(2,5-0,75\right):1,75\)
=1+1
=2

CM:A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + ... + \(\dfrac{1}{100^2}\) < 1
\(\dfrac{1}{2^2}\) = \(\dfrac{1}{2.2}\) < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}\) = \(\dfrac{1}{3.3}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)
\(\dfrac{1}{4^2}\) = \(\dfrac{1}{4.4}\) < \(\dfrac{1}{3.4}\) = \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)
\(\dfrac{1}{100^2}\) = \(\dfrac{1}{100.100}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}-\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + ... + \(\dfrac{1}{100^2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{100}\) < 1 (đpcm)
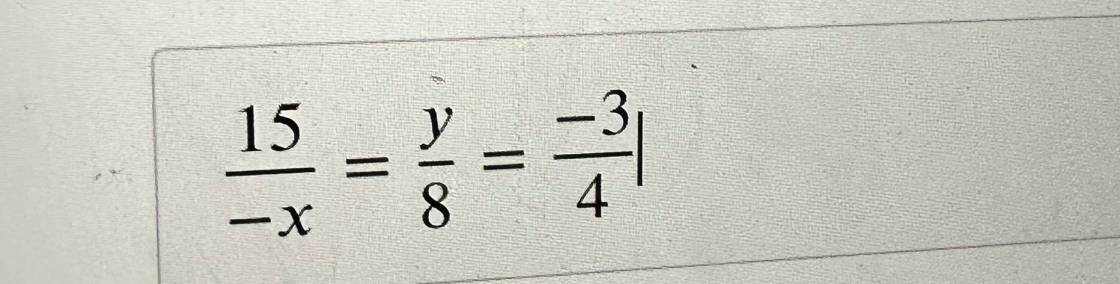

là sao???