3) Từ phần 2, ta có: \(B=\dfrac{3}{\sqrt x+1}\)

Khi đó: \(P=A\cdot B=\dfrac{\sqrt x+1}{\sqrt x+3}\cdot\dfrac{3}{\sqrt x+1}=\dfrac{3}{\sqrt x+3}\)

Vì x nguyên dương nên \(x\ge1\)

\(\Rightarrow \sqrt x\ge 1\)

\(\Rightarrow \sqrt x+3\ge 1+3=4\)

\(\Rightarrow \dfrac{1}{\sqrt x+3}\le\dfrac14\)

\(\Rightarrow \dfrac{3}{\sqrt x+3}\le \dfrac34\) hay \(P\le \dfrac34\)

Dấu "=" xảy ra khi: \(x=1\) (thỏa mãn ĐKXĐ)

$\text{#}Toru$

a: Thay x=9 vào B, ta được: \(B=\dfrac{\sqrt{9}}{\sqrt{9}+1}=\dfrac{3}{3+1}=\dfrac{3}{4}\)

b: \(P=A\cdot B\)

\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+2}-\dfrac{3\sqrt{x}}{x+\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-1-3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

c: \(m=\dfrac{1}{P}=\dfrac{\sqrt{x}+2}{\sqrt{x}}\) 

=>\(\sqrt{x}+2=m\cdot\sqrt{x}\)

=>\(\sqrt{x}\left(m-1\right)=2\)

Để \(m=\dfrac{1}{P}\) có nghiệm thì \(m-1\ne0\)

=>\(m\ne1\)

1: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1),(2) suy ra MO là đường trung trực của AB

=>MO\(\perp\)AB

Xét (O) có

ΔABQ nội tiếp

AQ là đường kính

Do đó: ΔABQ vuông tại B

=>AB\(\perp\)BQ

mà MO\(\perp\)AB

nên MO//BQ

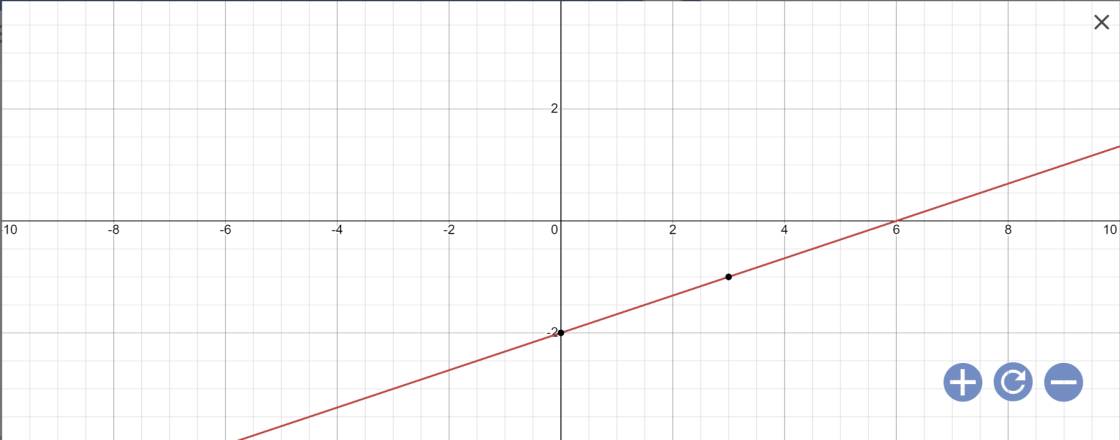
a: x-3y=6

=>x=3y+6

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=3y+6\end{matrix}\right.\)

Biểu diễn hình học:

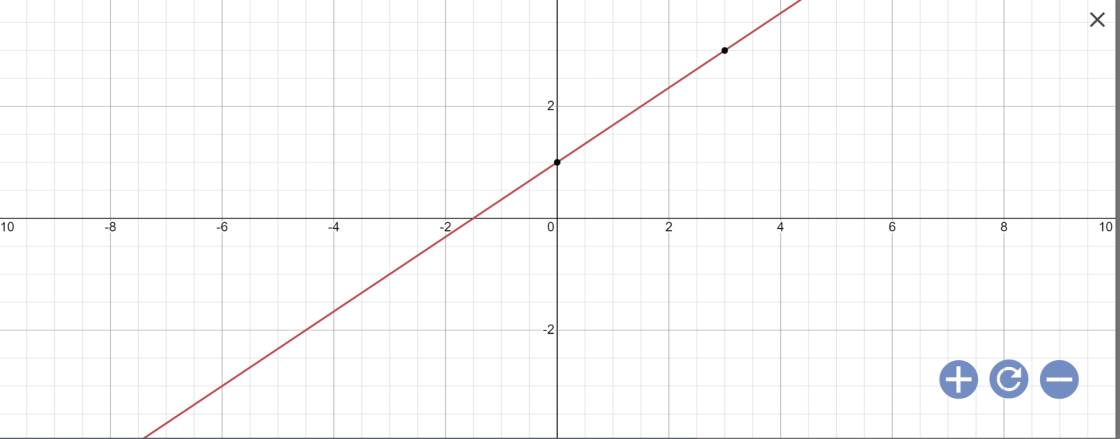
b: \(-2x+3y=3\)

=>\(3y=2x+3\)

=>\(y=\dfrac{2}{3}x+1\)

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x+1\end{matrix}\right.\)

Biểu diễn hình học:

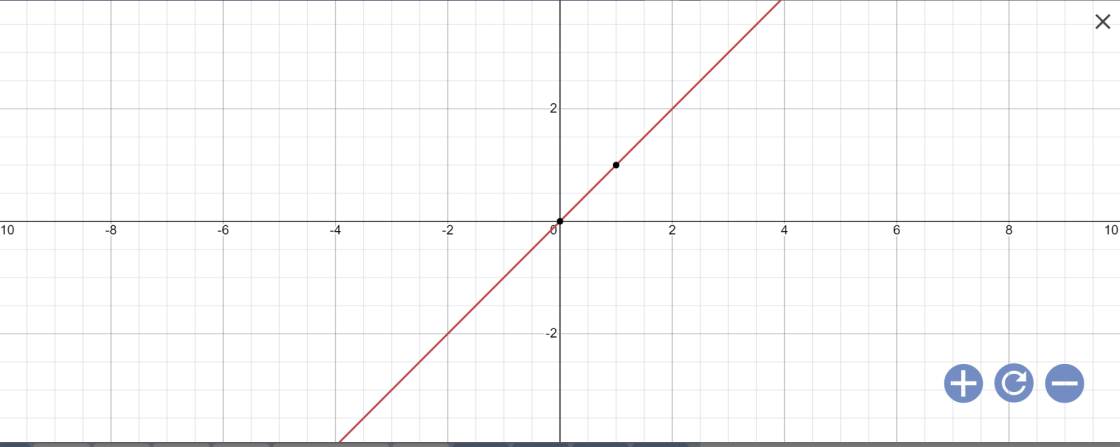
c: x-y=0

=>x=y

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=x\end{matrix}\right.\)

Biểu diễn hình học:

a. x=6+3y

b. x= 3/2y + 3/2

c. x=y

Để phương trình có hai nghiệm thì ∆ ≥ 0 nhé em

Vì nghiệm kép là hai nghiệm bằng nhau

\(VT=\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{3-2.\sqrt{3}.1+1}-\sqrt{3}\\ =\sqrt{\sqrt{3}^2-2.\sqrt{3}.1+1^2}-\sqrt{3}\\ =\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\\ =\left|\sqrt{3}-1\right|-\sqrt{3}\\ =\sqrt{3}-1-\sqrt{3}=-1=VP\left(DPCM\right)\)

Vậy: \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=-1\)

Phương trình bậc nhất hai ẩn có dạng : 

\(ax+by=c\left(a,b\ne0\right)\)

Chọn A