tìm x : 1/3 . x - 1/6 = 1/9 . x - 1/12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4\dfrac{7}{5741}\cdot\dfrac{1}{3759}-\dfrac{4}{3759}\cdot1\dfrac{2}{5741}+\dfrac{1}{3759}+\dfrac{1}{3759\cdot5741}\\ =\dfrac{22971}{5741}\cdot\dfrac{1}{3759}-\dfrac{1}{3759}\cdot\dfrac{22972}{5741}+\dfrac{1}{3759}\cdot\dfrac{5741}{5741}+\dfrac{1}{3759}\cdot\dfrac{1}{5741}\\ =\dfrac{1}{3759}\cdot\left(\dfrac{22971}{5741}-\dfrac{22972}{5741}+\dfrac{5741}{5741}+\dfrac{1}{5741}\right)\\ =\dfrac{1}{3759}\cdot\dfrac{5741}{5741}=\dfrac{1}{3759}\cdot1=\dfrac{1}{3759}\)

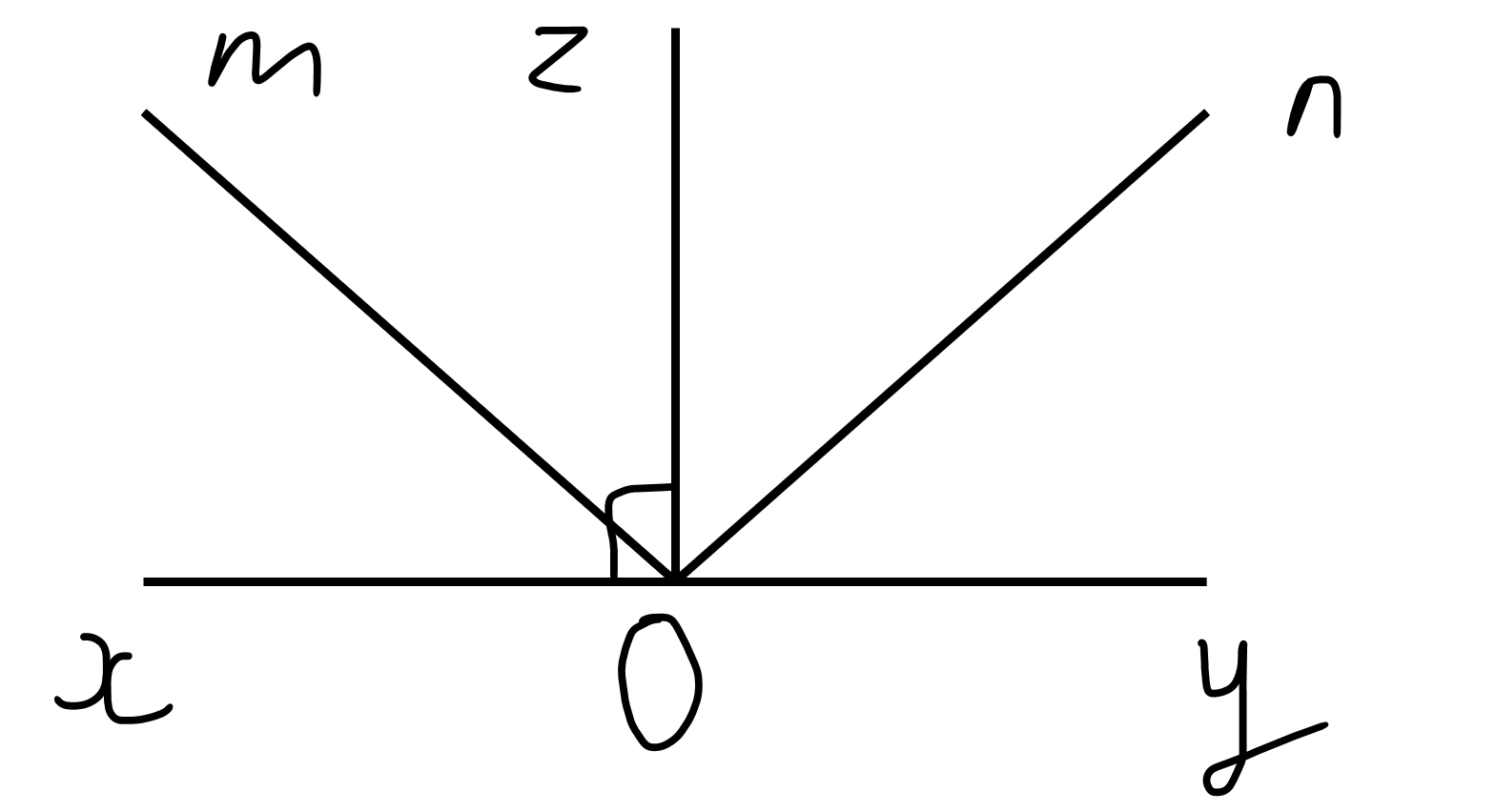
Cho góc bẹt xOy. Vẽ tia Oz thỏa mãn zOy = zOx. Gọi Om và On lần lượt là các tia phân giác của zOx;zOy a) Tính zOx;zOy b) zOm;zOn có phụ nhau không?
a) ta có: góc zOx + zOy = 180 độ
mà zOx = zOy
=> zOy + zOy = 180
2zOy = 180
zOy = 90
vậy zOy = zOx = 90
b) ta có: xOm + mOz = 90
mà xOm = mOz
=> 2mOz = 90
mOz = 45
vậy mOz = xOm = 45
ta có: nOy + nOz = 90
mà nOy = nOz
=> 2nOy = 90
nOy = 45
vậy nOy = nOz = 45
nOz + mOz = 45 + 45 = 90
vậy zOm; zOn có phụ nhau

\(\dfrac{5}{6}=\dfrac{5\times5}{6\times5}=\dfrac{25}{30}\)
\(1=\dfrac{30}{30}\)
4 phân số thỏa mãn đề bài là: \(\dfrac{26}{30};\dfrac{27}{30};\dfrac{28}{30};\dfrac{29}{30}\)

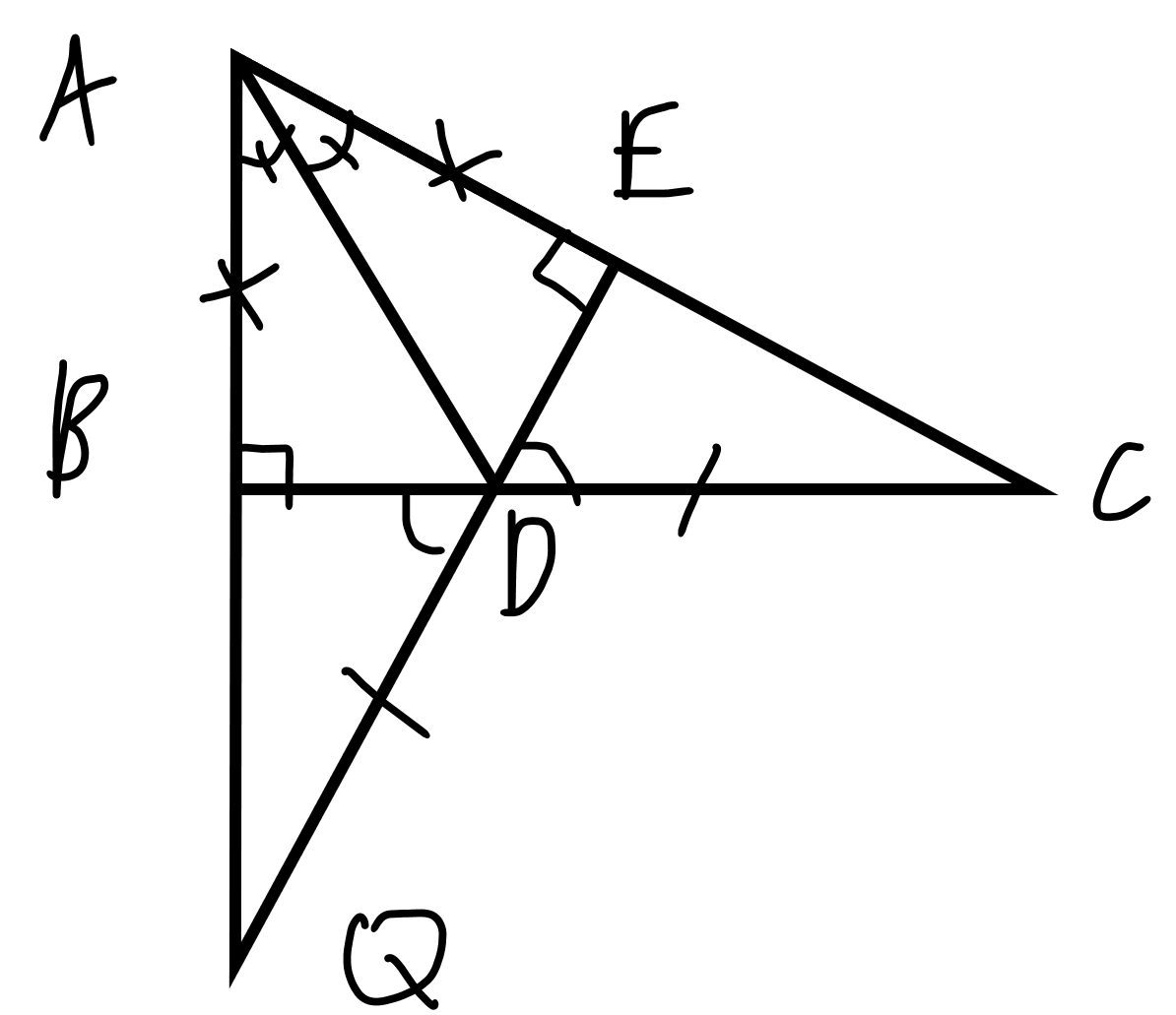
*chứng minh AB = AE
xét tam giác vuông ABD và tam giác vuông AED, có:
góc BAD = góc EAD (vì A là đường phân giác của tam giác ABC)
AD là cạnh chung
=> tam giác ABD = tam giác AED (ch-gn)
=> AB = AE (2 cạnh tương ứng)
*chứng minh DQ = CD
xét tam giác AEQ và tam giác ABC , có:
góc AEQ = góc ABC (= 90 độ)
AB = AE (câu a)
góc A là góc chung
=> tam giác AEQ = tam giác ABC (c-g-c)
=> QE = BC (1)
ta có: DC = BC - BD; DQ = QE - DE (2)
lại có: DB = DE (vì tam giác ABD = tam giác AED) (3)
=> TỪ (1) (2) (3) => DC = DQ

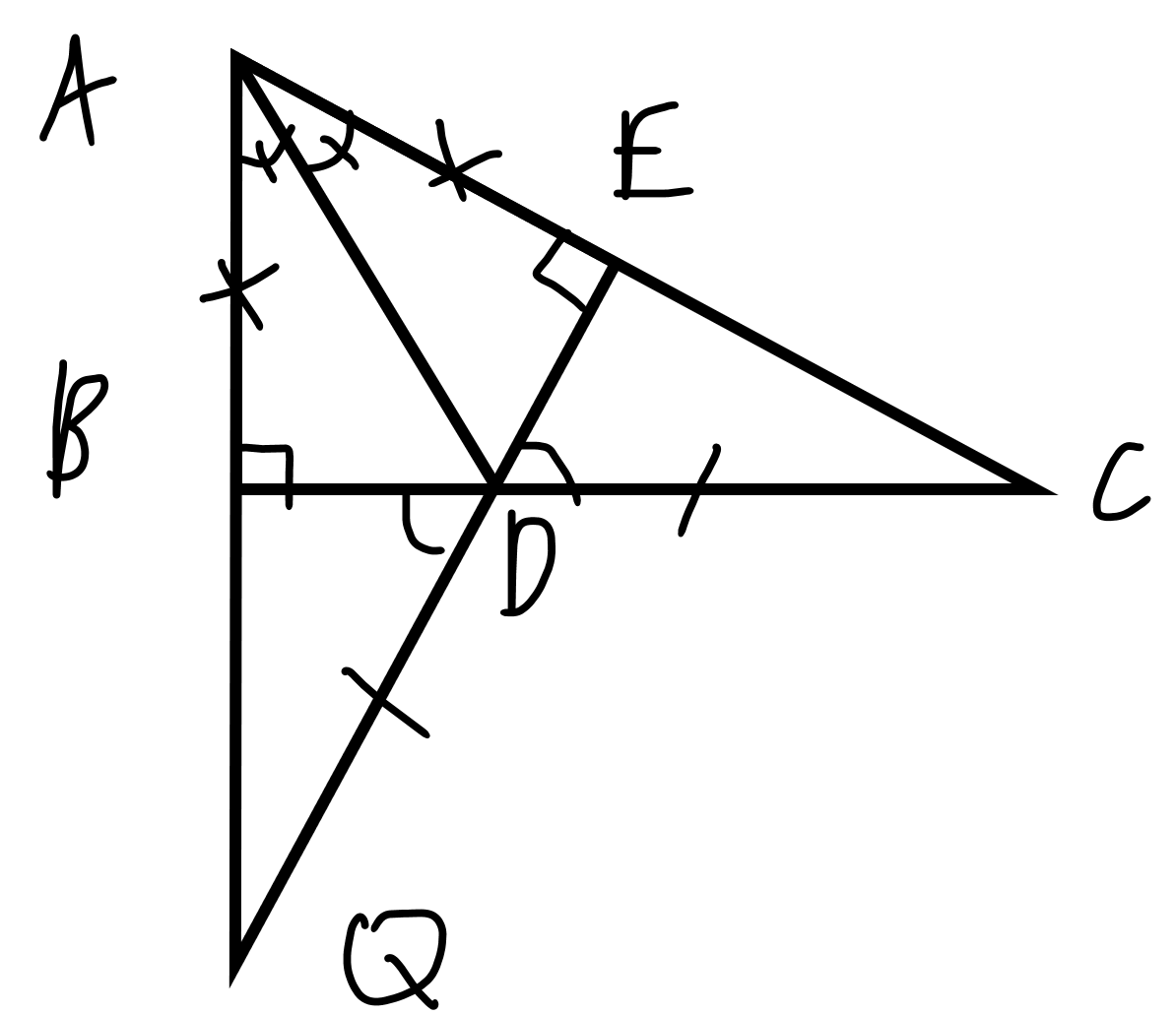
*chứng minh AB = AE
xét tam giác vuông ABD và tam giác vuông AED, có:
góc BAD = góc EAD (vì A là đường phân giác của tam giác ABC)
AD là cạnh chung
=> tam giác ABD = tam giác AED (ch-gn)
=> AB = AE (2 cạnh tương ứng)
*chứng minh DQ = CD
xét tam giác AEQ và tam giác ABC , có:
góc AEQ = góc ABC (= 90 độ)
AB = AE (câu a)
góc A là góc chung
=> tam giác AEQ = tam giác ABC (c-g-c)
=> QE = BC (1)
ta có: DC = BC - BD; DQ = QE - DE (2)
lại có: DB = DE (vì tam giác ABD = tam giác AED) (3)
=> TỪ (1) (2) (3) => DC = DQ


Câu 11:
\(C=\dfrac{\left|x-2017\right|+2018}{\left|x-2017\right|+2019}=\dfrac{\left|x-2017\right|+2019-1}{\left|x-2017\right|+2019}\\ =\dfrac{\left|x-2017\right|+2019}{\left|x-2017\right|+2019}-\dfrac{1}{\left|x-2017\right|+2019}\\ =1-\dfrac{1}{\left|x-2017\right|+2019}\)
Ta có: \(\left|x-2017\right|\ge0\forall x\Rightarrow\left|x-2017\right|+2019\ge2019\forall x\)
\(\Rightarrow\dfrac{1}{\left|x-2017\right|+2019}\le\dfrac{1}{2019}\forall x\)
\(\Rightarrow C=1-\dfrac{1}{\left|x-2017\right|+2018}\ge1-\dfrac{1}{2019}=\dfrac{2018}{2019}\)
Dấu "=" xảy ra khi: \(x-2017=0\Rightarrow x=2017\)
vậy: ...

a) Gọi K' là giao điểm của BI và EF, S là giao điểm của EJ và AB.
Ta có \(\left(FSBA\right)=-1\) (hàng điều hòa quen thuộc). Mặt khác, dễ thấy K'B là trung trực của FJ nên K'B cũng là tia phân giác của \(\widehat{FK'S}\)
Do đó, \(\widehat{AK'B}=90^o\). Khi đó tam giác AK'B vuông tại K' có trung tuyến K'M nên \(K'M=MB=\dfrac{1}{2}AB\)
Từ đó suy ra tam giác MK'B cân tại M \(\Rightarrow\widehat{MK'B}=\widehat{MBK'}=\widehat{K'BC}\)
Do đó MK'//BC. Chú ý rằng MN là đường trung bình của tam giác ABC \(\Rightarrow\) MN//BC. Vậy \(K'\in MN\) hay K' chính là giao điểm của MN và JE. Điều này có nghĩa là \(K'\equiv K\).
Như vậy, \(K,B,I\) thẳng hàng và \(\widehat{AKB}=90^o\) hay \(AK\perp BI\)
Lại có \(FJ\perp BI\) nên AK//FJ hay AK//HJ.
Tương tự, ta cũng có AH//KJ nên tứ giác AKJH là hình bình hành.
\(\Rightarrow\) HK, AJ cắt nhau tại trung điểm mỗi đoạn, hay JA đi qua trung điểm của HK.
câu a ý 2:
Gọi U là giao điểm của EF và BC, P là trung điểm BC, X là điểm chính giữa cung BC không chứa D của (O).
Có \(\widehat{XIB}=\widehat{IAB}+\widehat{IBA}=\widehat{XCB}+\widehat{IBC}=\widehat{XBC}+\widehat{IBC}=\widehat{XBI}\) nên tam giác XBI cân tại X \(\Rightarrow XB=XI\)
Tương tự, ta cũng có \(XB=XC=XI\) nên X là tâm (IBC)
Dễ thấy \(\widehat{XBD}=\widehat{XCD}=90^o\) nên XB, XC là tiếp tuyến tại B và C của (X).
\(\Rightarrow DC^2=DP.DX=DT.DG\) \(\Rightarrow\) Tứ giác TPXG nội tiếp.
\(\Rightarrow\widehat{DPT}=\widehat{XGT}=\widehat{XTG}=\widehat{XPG}\)
\(\Rightarrow90^o-\widehat{DPT}=90^o-\widehat{XPG}\)
\(\Rightarrow\widehat{UPT}=\widehat{UPG}\) . Do \(\widehat{UPG}+\widehat{GPC}=180^o\)
\(\Rightarrow\) \(\widehat{GPC}+\widehat{UPT}=180^o\)
Vì D là giao điểm của 2 tiếp tuyến tại B và C của đường tròn (X) nên GD là đối trung của tam giác GBC
\(\Rightarrow\widehat{BGT}=\widehat{PGC}\)
Lại có \(\widehat{GTB}=\widehat{GCP}\) \(\Rightarrow\Delta GTB\sim\Delta GCP\) \(\Rightarrow\widehat{GBT}=\widehat{GPC}\)
Lại có \(\widehat{GBT}=\widehat{GIT}\) nên \(\widehat{GPC}=\widehat{GIT}\)
Kết hợp với \(\widehat{GPC}+\widehat{UPT}=180^o\), ta có \(\widehat{GIT}+\widehat{UPT}=180^o\)
\(\Rightarrow\) Tứ giác ITPJ nội tiếp.
Mặt khác, \(\left(BCJU\right)=-1\) và P là trung điểm BC nên \(\overline{UJ}.\overline{UP}=\overline{UB}.\overline{UC}\) (hệ thức Maclaurin)
\(\Rightarrow P_{U/\left(ITPJ\right)}=P_{U/\left(X\right)}\)
\(\Rightarrow\) U nằm trên trục đẳng phương của đường tròn (ITPJ) và (X), mà IT là trục đẳng phương của 2 đường tròn này nên U, I, T thẳng hàng.
Xét cực và đối cực đối với (I). Kí hiệu \(d_Y\) là đối cực của Y đối với (I).
Ta có \(\left(BCJU\right)=-1\) \(\Rightarrow J\in d_U\)
Lại có \(U\in EF\equiv d_A\Rightarrow A\in d_U\)
Do đó \(JA\equiv d_U\) \(\Rightarrow JA\perp UI\) hay \(JA\perp IT\) (đpcm)
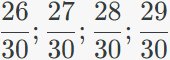


\(\dfrac{1}{3}\cdot x-\dfrac{1}{6}=\dfrac{1}{9}\cdot x-\dfrac{1}{12}\)
\(\dfrac{1}{9}\cdot x-\dfrac{1}{3}\cdot x=-\dfrac{1}{6}+\dfrac{1}{12}\)
\(-\dfrac{2}{9}\cdot x=-\dfrac{2}{12}+\dfrac{1}{12}\)
\(-\dfrac{2}{9}\cdot x=-\dfrac{1}{12}\)
\(x=-\dfrac{1}{12}:\dfrac{-2}{9}\)
\(x=\dfrac{3}{8}\)
\(\dfrac{1}{3}\cdot x-\dfrac{1}{6}=\dfrac{1}{9}\cdot x-\dfrac{1}{12}\\ \dfrac{1}{3}\cdot x-\dfrac{1}{9}\cdot x=\dfrac{1}{6}-\dfrac{1}{12}\\ x\cdot\left(\dfrac{1}{3}-\dfrac{1}{9}\right)=\dfrac{1}{6}-\dfrac{1}{12}\\ x\cdot\dfrac{2}{9}=\dfrac{1}{12}\\ x=\dfrac{1}{12}:\dfrac{2}{9}=\dfrac{1}{12}\cdot\dfrac{9}{2}\\ x=\dfrac{3}{8}\)