Giải hệ phương trình: x(x-3y)=4(y^(2)+2) và (xy-4)(x+y)=8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay x=1 và y=-5 vào hệ, ta được:
\(\left\{{}\begin{matrix}3a\cdot1-\left(b+1\right)\cdot\left(-5\right)=93\\-5\cdot b+4\cdot a\cdot1=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a+5\left(b+1\right)=93\\4a-5b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a+5b=88\\4a-5b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7a=85\\3a+5b=88\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{85}{7}\\5b=88-3a=88-3\cdot\dfrac{85}{7}=\dfrac{361}{7}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{85}{7}\\b=\dfrac{361}{35}\end{matrix}\right.\)
b: Thay x=3 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}\left(a-2\right)\cdot3+5b\cdot\left(-1\right)=25\\2a\cdot3-\left(-1\right)\left(b-2\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a-6-5b=25\\6a+b-2=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a-5b=31\\6a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-10b=62\\6a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-11b=55\\6a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-5\\6a=7-b=7-\left(-5\right)=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-5\\a=2\end{matrix}\right.\)

\(B=\left(\dfrac{x+2\sqrt{x}}{\sqrt{x}}+\sqrt{x}-2\right):\sqrt{x}\left(x>0\right)\\ =\left[\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}}+\sqrt{x}-2\right].\dfrac{1}{\sqrt{x}}\\ =\left(\sqrt{x}+2+\sqrt{x}-2\right).\dfrac{1}{\sqrt{x}}\\ =\dfrac{2\sqrt{x}}{\sqrt{x}}=2\)

Nếu bạn không dùng đến điểm O thì theo mình nghĩ sẽ không sao bạn nhé! Tuy nhiên để giải toán chắc chắn và chính xác chúng mình nên vẽ hình theo dữ kiện đề bài cho!
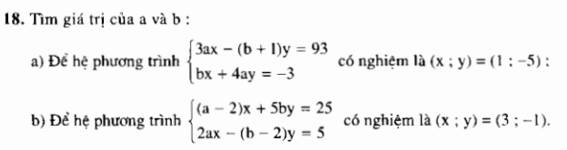
Ta có: \(\left\{{}\begin{matrix}x\left(x-3y\right)=4\left(y^2+2\right)\left(1\right)\\\left(xy-4\right)\left(x+y\right)=8\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Rightarrow xy-4;x+y\ne0\)
\(\left(1\right)\Leftrightarrow x^2-3xy-4y^2=8\) (*)
Từ (*) và (2) \(\Rightarrow x^2-3xy-4y^2=\left(xy-4\right)\left(x+y\right)\)
\(\Leftrightarrow x\left(x-4y\right)+y\left(x-4y\right)=\left(xy-4\right)\left(x+y\right)\)
\(\Leftrightarrow\left(x+y\right)\left(x-4y\right)=\left(x+y\right)\left(xy-4\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\left(L\right)\\x-4y=xy-4\end{matrix}\right.\) \(\Leftrightarrow x\left(1-y\right)+4\left(1-y\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(1-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\y=1\end{matrix}\right.\)
x = -4 thay vào (*), ta được: \(16-3.\left(-4\right)y-4y^2=8\)
\(\Leftrightarrow8+12y-4y^2=0\) \(\Leftrightarrow y^2-3y-2=0\)
\(\Leftrightarrow y=\dfrac{3\pm\sqrt{17}}{2}\) ( dùng \(\Delta\) )
y=1 thay vào (*), ta được: \(x^2-3x-4=8\)
\(\Leftrightarrow x^2-3x-12=0\) \(\Leftrightarrow x=\dfrac{3\pm\sqrt{57}}{2}\)
Vậy ...