Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) x² + 2xy + y² - x - y
= (x² + 2xy + y²) - (x + y)
= (x + y)² - (x + y)
= (x + y)(x + y + 1)
b) 2x³ + 6x² + 12x + 8
= 2(x³ + 3x² + 6x + 4)
= 2(x³ + x² + 2x² + 2x + 4x + 4)
= 2[(x³ + x²) + (2x² + 2x) + (4x + 4)]
= 2[x²(x + 1) + 2x(x + 1) + 4(x + 1)]
= 2(x + 1)(x² + 2x + 4)
Xét có // nên theo định lí Thalès ta có
. (1)
Xét có // nên theo định lí Thalès ta có
. (2)
Xét có // nên theo định lí Thalès ta có
. (3)
Từ , , suy ra .
Suy ra .
Xét có // nên theo định lí Thalès ta có
. (1)
Xét có // nên theo định lí Thalès ta có
. (2)
Xét có // nên theo định lí Thalès ta có
. (3)
Từ , , suy ra .
Suy ra .
Do AB//CD( vì cùng vuông góc với BD)
Nên áp dụng định lí Ta lét , ta được :
EB/ED=AB/CD
=> EB/6 = 150/4
=> EB = 150.6/4 = 225 (cm)
Đổi đơn vị: m cm.
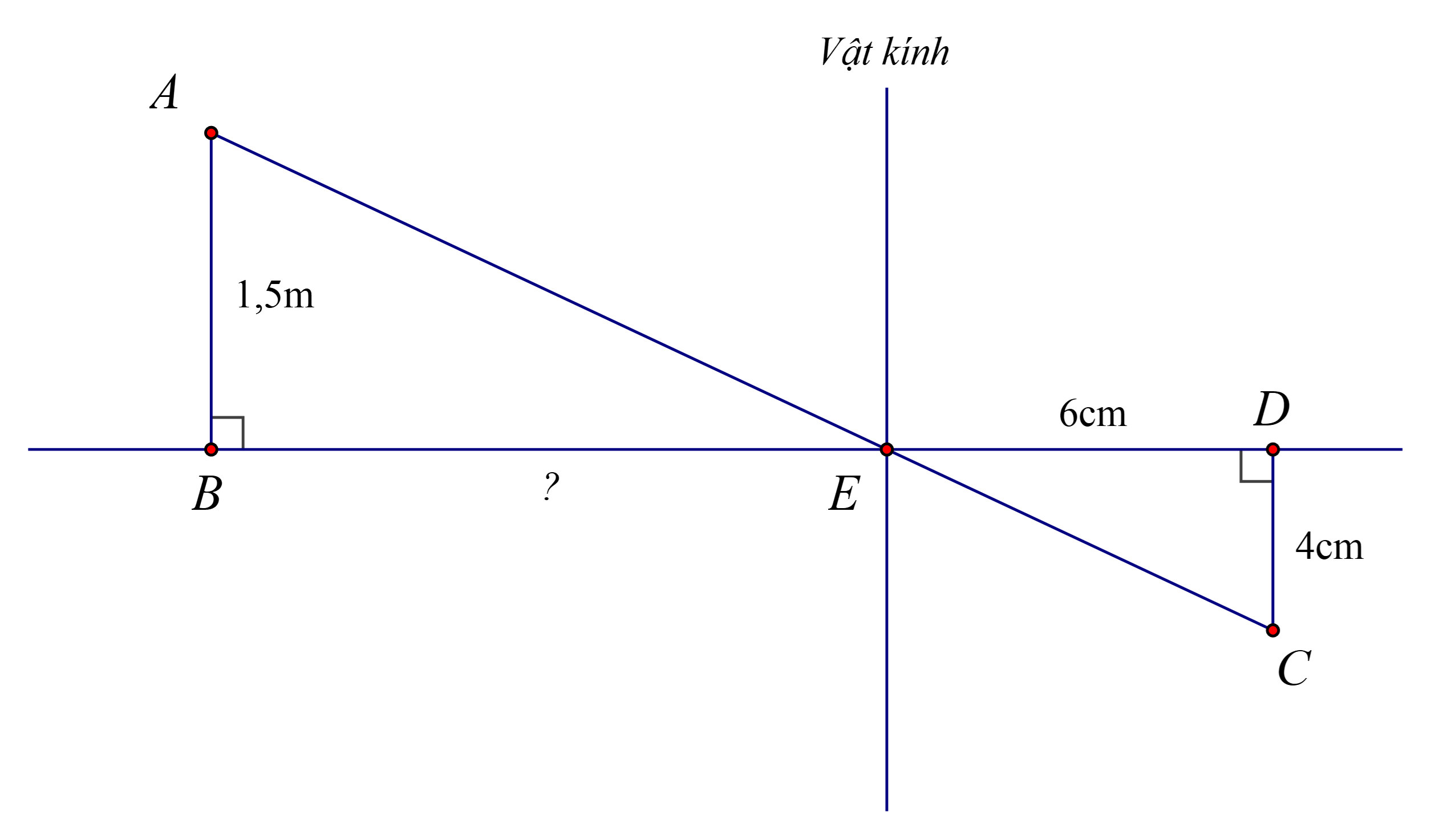
Ta có // (cùng vuông góc ) suy ra (định lí Thalès)
Suy ra (cm).
Vậy người đứng cách vật kính máy ảnh là cm.
Lời giải:
a. Vì $A,D$ đối xứng nhau qua $M$ nên $M$ là trung điểm $AD$
Tứ giác $ABDC$ có 2 đường chéo $AD, BC$ cắt nhau tại trung điểm $M$ của mỗi đường nên là hình bình hành.
Mà $\widehat{BAC}=90^0$ nên $ABDC$ là hình chữ nhật.
b.
Vì $ABDC$ là hcn nên:
$AB\parallel DC, AB=DC$ (1)
Vì $E$ đối xứng với $A$ qua $B$ nên $A,B,E$ thẳng hàng và $AB=BE$(2)
Từ $(1); (2)\Rightarrow BE\parallel DC, BE=DC$
Tứ giác $BEDC$ có 2 cạnh đối nhau $BE, DC$ song song và bằng nhau nên $BEDC$ là hình bình hành.
c.
$BEDC$ là hbh nên $BC\parallel ED$ và $BC=ED$
Ta có:
$BC=ED$, mà $BC=2BM$ nên $ED=2BM$
$BC\parallel ED\Rightarrow BM\parallel ED$. Áp dụng định lý Talet:
$\frac{EK}{KM}=\frac{ED}{BM}=\frac{2BM}{BM}=2$
$\Rightarrow EK=2KM$ (đpcm)
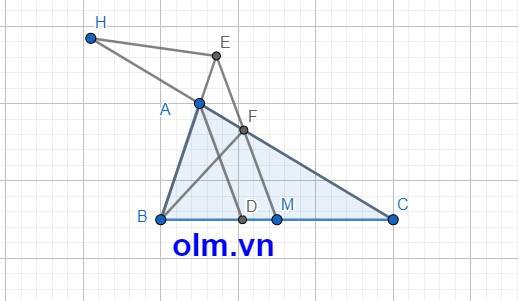
Kéo dài AC về phía A lấy điểm H sao cho CF = FH;
Lúc này bài toán trở thành chứng minh BE = HF
Xét tam giác HBC có: MB = MC (gt); FH = FC
Nên MF là đường trung bình của tam giác HBC ⇒ ME//BH
Mặt khác ta có ME//AD ⇒ \(\widehat{AEF}\) = \(\widehat{BAD}\) (hai góc đồng vị) (1)
\(\widehat{BAD}\) = \(\widehat{DAF}\) (AD là phân giác của góc BAC) (2)
\(\widehat{DAF}\) = \(\widehat{AFE}\) (hai góc so le trong) (3)
Kết hợp (1);(2);(3) ta có: \(\widehat{AEF}\) = \(\widehat{AFE}\) ⇒ \(\Delta\)AEF cân tại A ⇒ AE = AF (*)
Vì ME//HB nên: \(\widehat{AHB}\) = \(\widehat{AFE}\) (so le trong)
\(\widehat{ABH}\) = \(\widehat{AEF}\) (so le trong)
⇒ \(\widehat{AHB}\) = \(\widehat{ABH}\) ⇒ \(\Delta\) AHB cân tại A ⇒ AB = AH (**)
Cộng vế với vế của(*) và(*) ta có: AE + AB = AF + AH
⇒ BE = FH
⇒ BE = CF (vì cùng bằng HF)
a) x - 3 = (3 - x)²
x - 3 = (x - 3)²
x - 3 - (x - 3)² = 0
(x - 3)[1 - (x - 3)] = 0
(x - 3)(1 - x + 3) = 0
(x - 3)(4 - x) = 0
x - 3 = 0 hoặc 4 - x = 0
*) x - 3 = 0
x = 3
*) 4 - x = 0
x = 4
Vậy x = 3; x = 4
b) x³ + 3/2 x² + 3/4 x + 1/8 = 1/64
(x + 1/2)³ = 1/64
(x + 1/2)³ = (1/4)³
x + 1/2 = 1/4
x = 1/4 - 1/2
x = -1/2
a) Ta có: �−3=(3−�)2x−3=(3−x)2
(�−3)−(�−3)2=0(x−3)−(x−3)2=0
(�−3)(4−�)=0(x−3)(4−x)=0
�∈{3;4}x∈{3;4}.
b) Ta có: �3+32�2+34�+18=164x3+23x2+43x+81=641
(�+12)3=(14)3(x+21)3=(41)3
�+12=14x+21=41
�=−14x=4−1.