Câu c hơi mờ em ghi lại xíu là chứng tỏ răng f(x) vô nghiệm với mọi x nha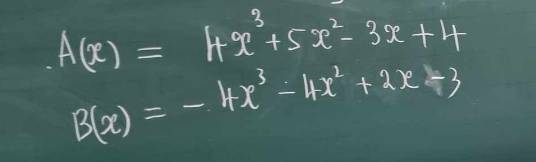
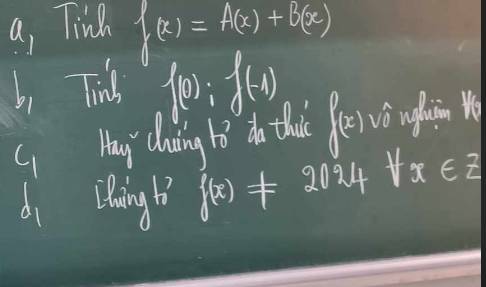
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay x=-2 và y=2 vào M, ta được:
\(M=2\cdot\left(-2\right)\cdot2-4\cdot\left(-2\right)+5\)
=-8+8+5
=5

\(x\left(x+11\right)-x^2+x=12\)
=>\(x^2+11x-x^2+x=12\)
=>12x=12
=>x=1

Câu 1: B
Câu 2: D
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7:D
Câu 8: C

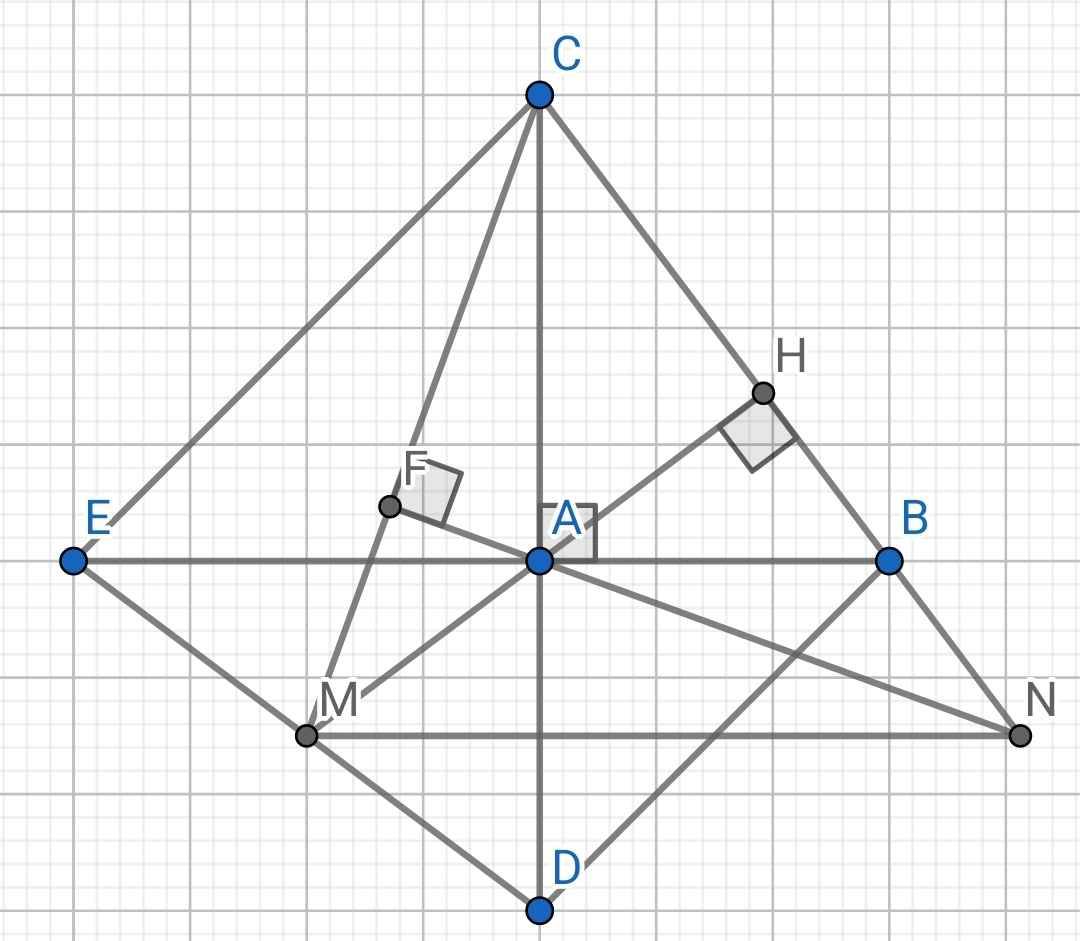
a) Do ∆ADB vuông cân tại A (gt)
⇒ AB = AD
Do ∆AEC vuông cân tại A (gt)
⇒ AE = AC
Xét hai tam giác vuông: ∆ABC và ∆ADE có:
AB = AD (cmt)
AC = AE (cmt)
∆ABC = ∆ADE (hai cạnh góc vuông)
⇒ BC = DE (hai cạnh tương ứng)
b) Do ∆ADE vuông cân tại A (gt)
⇒ ∠ADB = ∠ABD = 45⁰
Do ∆AEC vuông cân tại A (gt)
⇒ ∠ACE = ∠AEC = 45⁰
⇒ ∠ACE = ∠ADB = 45⁰
Mà ∠ACE và ∠ADB là hai góc so le trong
⇒ DB // EC
c) Do AH ⊥ BC (gt)
⇒ MH ⊥ CN
Do AF ⊥ MC (gt)
⇒ NF ⊥ MC
∆CMN có:
MH ⊥ CN (cmt)
NF ⊥ MC (cmt)
⇒ MH và NF là hai đường cao của ∆CMN
Mà MH cắt NF tại A
⇒ CA là đường cao thứ ba của ∆CMN
⇒ CA ⊥ MN
d) Em xem lại đề nhé

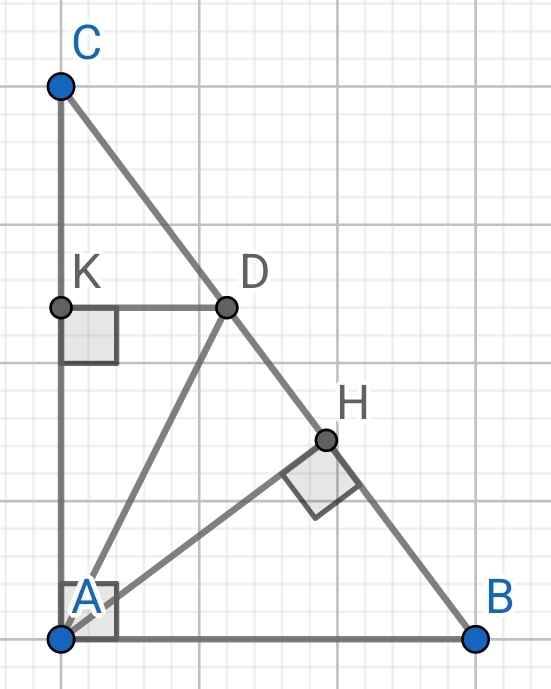
a) ∆ABD có:
BA = BD (gt)
⇒ ∆ABD cân tại B
⇒ ∠BAD = ∠BDA
b) Do DK ⊥ AC (gt)
AB ⊥ AC (do ∆ABC vuông tại A)
⇒ DK // AB
⇒ ∠ADK = ∠BAD (so le trong)
Mà ∠BAD = ∠BDA (cmt)
⇒ ∠ADK = ∠BDA
⇒ ∠ADK = ∠HDA
Xét hai tam giác vuông: ∆ADK và ∆ADH có:
AD là cạnh chung
∠ADK = ∠HDA (cmt)
⇒ ∆ADK = ∆ADH (cạnh huyền - góc nhọn)
⇒ ∠DAK = ∠DAH (hai góc tương ứng)
⇒ ∠DAC = ∠DAH
⇒ AD là tia phân giác của ∠HAC
c) Do ∆ADK = ∆ADH (cmt)
⇒ AK = AH (hai cạnh tương ứng)
d) ∆CDK vuông tại K
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CK < CD
Mà AK = AH (cmt)
BA = BD (cmt)
Cộng vế với vế, ta có:
CK + AK + AB < CD + AH + BD
⇒ AB + AC < BC + AH
a: Xet ΔBAD có BA=BD
nên ΔBAD cân tại B
=>\(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔDHA vuông tại H)
\(\widehat{DAC}+\widehat{BAD}=90^0\)
mà \(\widehat{BDA}=\widehat{BAD}\)
nên \(\widehat{HAD}=\widehat{DAC}\)
=>AD là phân giác của góc HAC
c: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔAHD=ΔAKD
=>AH=AK
d: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>\(AH\cdot BC=AB\cdot AC\)
\(\left(AB+AC\right)^2-\left(BC+AH\right)^2\)
\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-AH^2-2\cdot BC\cdot AH\)
\(=BC^2+2\cdot AH\cdot BC-BC^2-2\cdot BC\cdot AH-AH^2\)
\(=-AH^2< 0\)
=>\(\left(AB+AC\right)^2< \left(BC+AH\right)^2\)
=>AB+AC<BC+AH


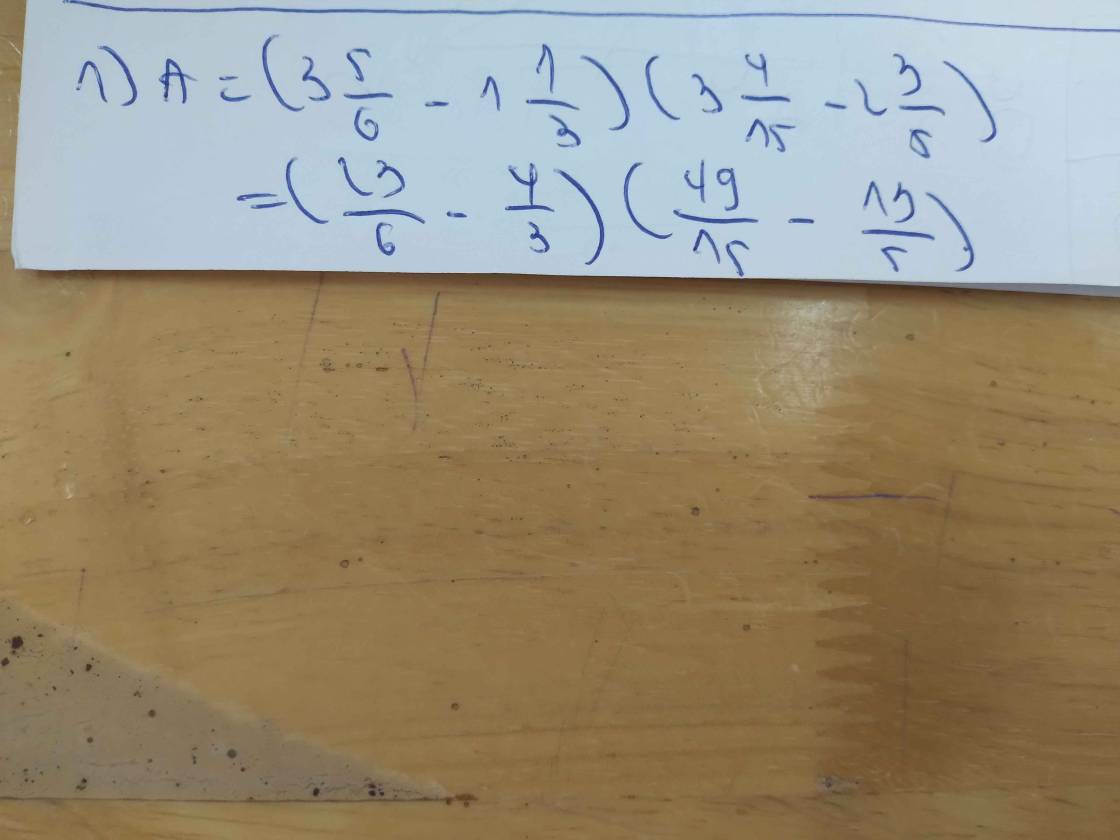

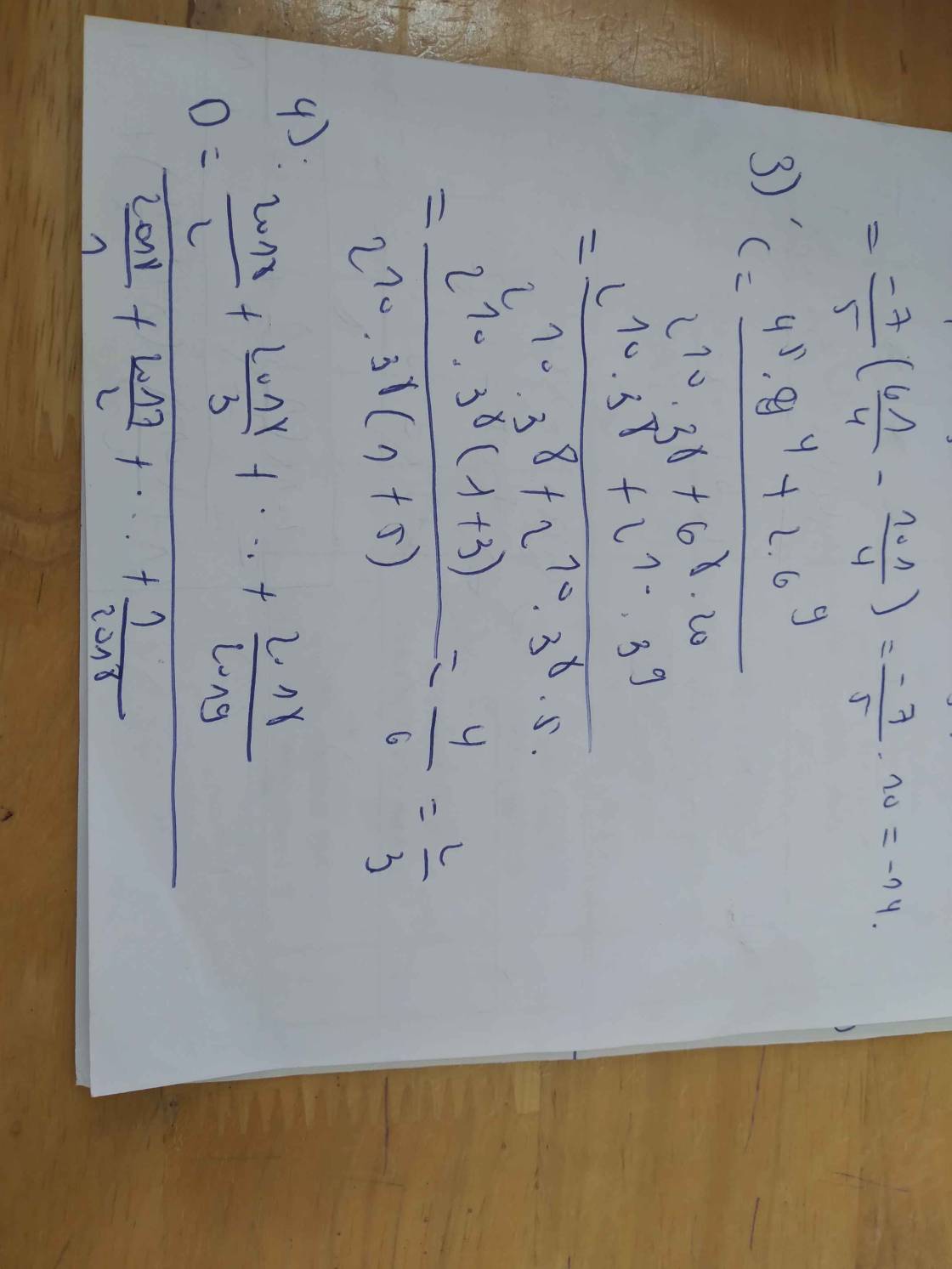

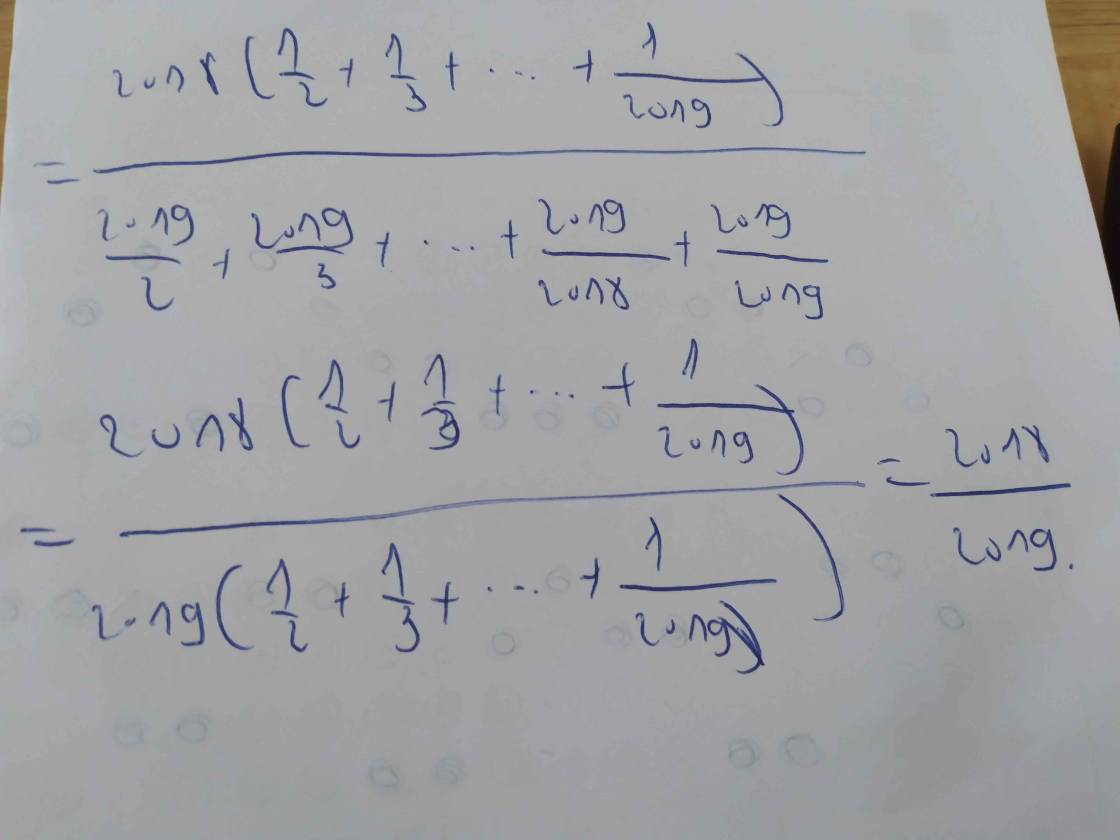
a: f(x)=A(x)+B(x)
\(=4x^3+5x^2-3x+4-4x^3-4x^2+2x-3\)
\(=x^2-x+1\)
b: \(f\left(0\right)=0^2-0+1=1\)
\(f\left(1\right)=1^2-1+1=1\)
c: Đặt f(x)=0
=>\(x^2-x+1=0\)
=>\(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=0\)
=>\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\)(vô lý)
=>f(x) không có nghiệm
c: Đặt f(x)=2024
=>\(x^2-x+1=2024\)
=>\(x^2-x-2023=0\)(1)
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-2023\right)=8093>0\)
Do đó: Phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-\sqrt{8093}}{2}\notin Z\\x_2=\dfrac{1+\sqrt{8093}}{2}\notin Z\end{matrix}\right.\)
=>f(x) luôn khác 2024 với mọi số nguyên x