Thay mỗi chữ dưới đây bởi chữ số thích hợp :ab.caa+cb.aba=bd.ba0 giải chi tiết nhé!cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số bị che mờ và viết lằng nhằng là số 454
Chọn: A: 454


ABCD là hình vuông nên OA=OC => d( A,(SBD) ) = d( C,(SBD) )
Kẻ AH vuông SO
BD vuông AO, BD vuông SA nên BD vuông (SAO) => BD vuông AH
=> AH vuông (SBD)
=> d( A,(SBD) ) = AH
Xét SAO : \(\dfrac{1}{AH^2}\) = \(\dfrac{1}{SA^2}\) + \(\dfrac{1}{AO^2}\)
SA = 3a, AO = \(a\sqrt{2}\) => AH = \(\dfrac{3a\sqrt{22}}{11}\)
Vậy khoảng cách từ C đến (SBD) = \(\dfrac{3a\sqrt{22}}{11}\)

27 x 37 + 27 x 63
= 27 x (37 + 63)
= 27 x 100
= 2700

a: Vì AI và AE là hai tia đối nhau
nên A nằm giữa E và I
b: A nằm giữa E và I
=>IE=IA+AE=4+2=6(cm)
c: Vì AK và AI là hai tia đối nhau
nên A nằm giữa K và I
ta có: A nằm giữa K và I
mà AK=AI(=2cm)
nên A là trung điểm của KI
d: 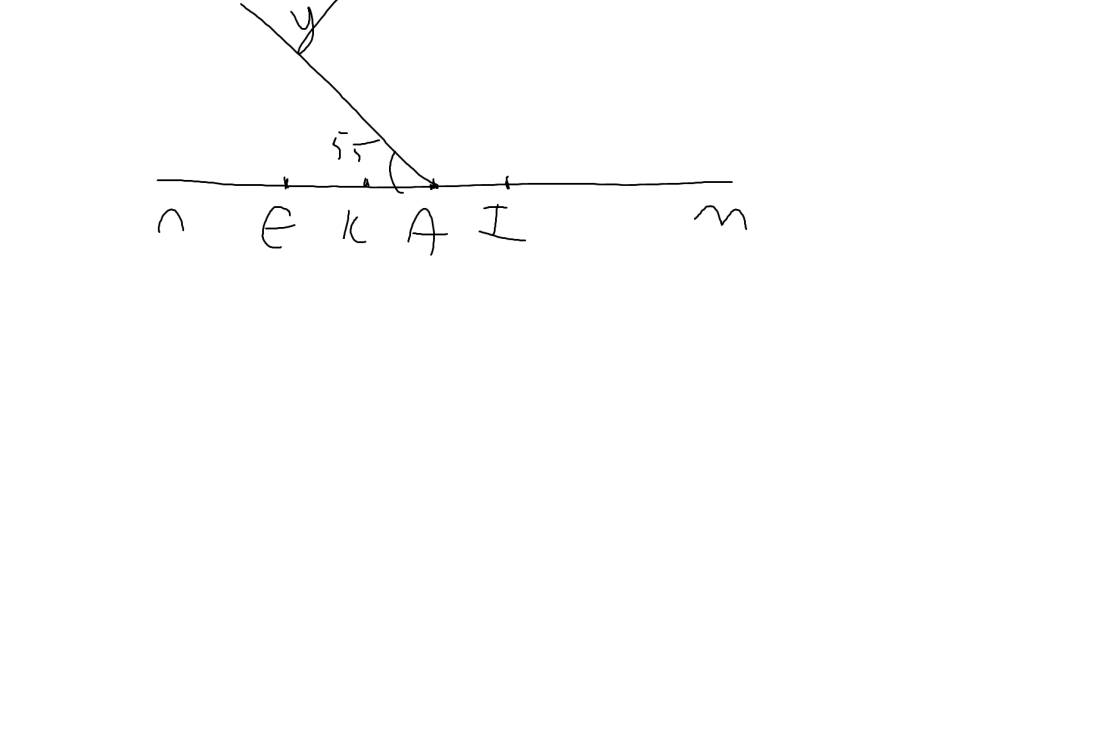

\(E=\dfrac{10n+6}{2n-3}=\dfrac{10n-15+21}{2n-3}=5+\dfrac{21}{2n-3}\)
Để E có giá trị lớn nhất thì \(\dfrac{21}{2n-3}\) max
=>2n-3=1
=>2n=4
=>n=2
Để E min thì 2n-3=-1
=>2n=2
=>n=1
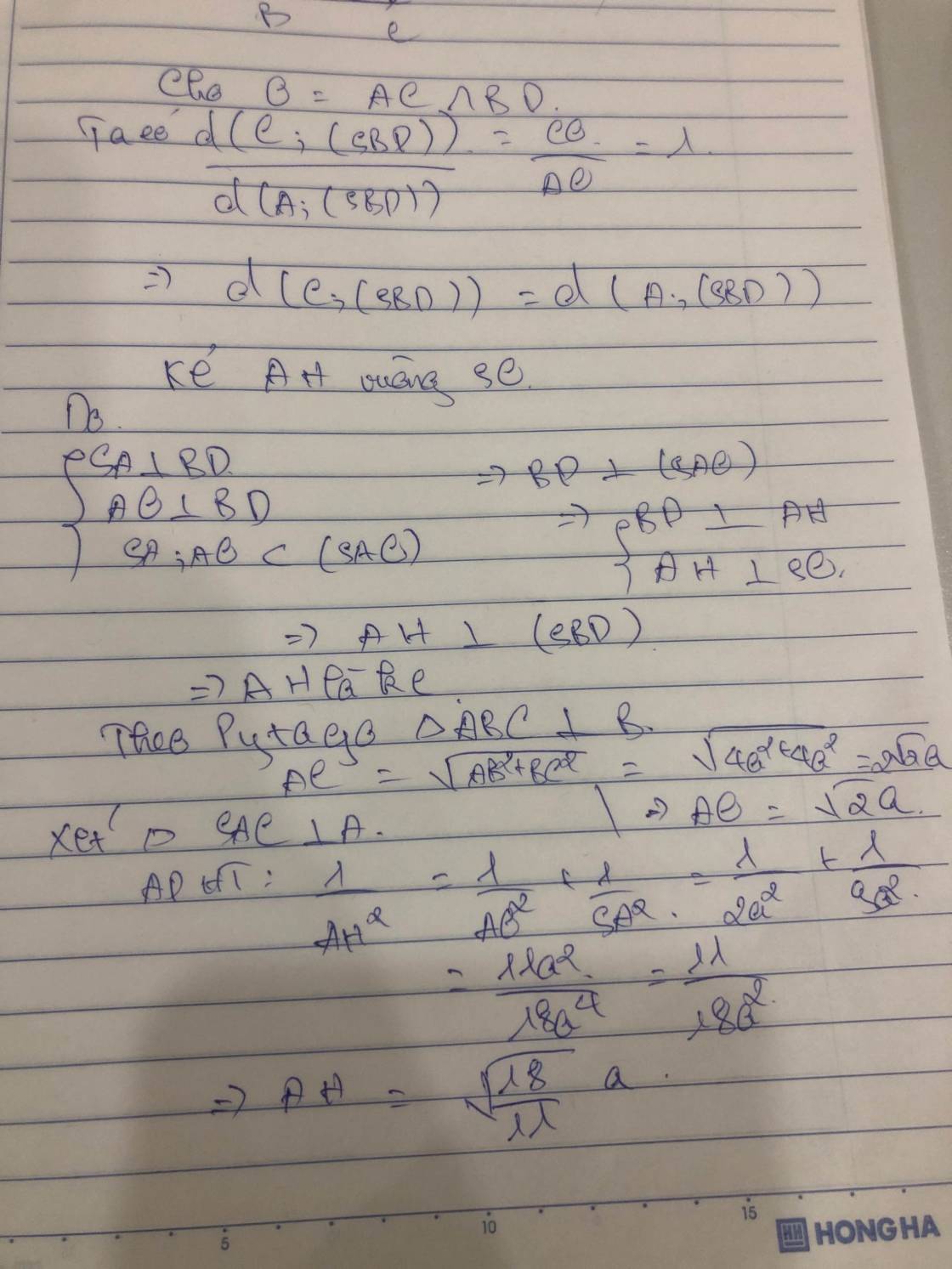
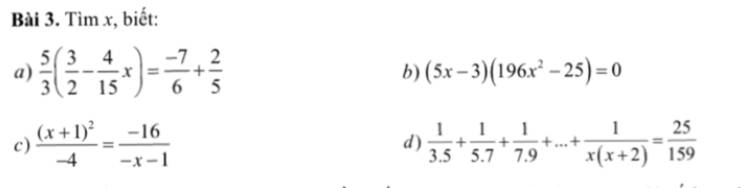




\(\overline{ab,caa}+\overline{cb,aba}=\overline{bd,ba0}\)
\(\Rightarrow\overline{abcaa}+\overline{cbaba}=\overline{bdba0}\) (nhân 2 vế với 1000)
\(VP⋮10\Rightarrow VT⋮10\Rightarrow a=0\) hoặc \(a=5\)
Với \(a=0\)
\(\Rightarrow\overline{bc00}+\overline{cb0b0}=\overline{bdb00}\)
\(VP⋮100\Rightarrow VT⋮100\) mà \(\overline{bc00}⋮100\Rightarrow\overline{cb0b0}⋮100\Rightarrow b=0\)
\(\Rightarrow\overline{c00}+\overline{c0000}=\overline{d000}\) do VP là số có 4 chữ số nên trường hợp a=0 bị loại
Với \(a=5\)
\(\Rightarrow\overline{5bc55}+\overline{cb5b5}=\overline{bdb50}\)
\(\Rightarrow1000x\overline{5bc}+55+1000x\overline{cb5}+\overline{b5}=\overline{bdb50}\)
\(VP⋮25\Rightarrow VT⋮25\) mà \(1000x\overline{5bc}⋮25;1000x\overline{cb5}⋮25\Rightarrow55+\overline{b5}⋮25\)
\(55+\overline{b5}=55+10xb+5=10xb+50+10\)
\(50⋮25\Rightarrow10xb+10⋮25\Rightarrow b=4\) hoặc \(b=9\)
Với \(b=4\)
\(\Rightarrow\overline{54c55}+\overline{c4545}=\overline{4d450}\) Ta thấy \(\overline{54c55}>\overline{4d450}\)
=> b=4 loại
Với \(b=9\)
\(\Rightarrow\overline{59c55}+\overline{c9595}=\overline{9d950}\)
\(\Rightarrow59055+100xc+10000xc+9595=90950+1000xd\)
\(10100xc=22300+1000xd\)
\(101xc=223+10xd\)
\(\Rightarrow\overline{c0c}-223=10xd\)
\(10xd⋮10\Rightarrow\overline{c0c}-223⋮10\Rightarrow c=3\)
\(\Rightarrow101xc-223=101x3-223=80=10xd\Rightarrow d=8\)
Thử
59355+39595=98950 Thỏa mãn đề bài
Kết luận: a=5; b=9; c=3; d=8