A=(x-1)^10+(y-3)^10+2024
tìm giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B=1-2-3+4+5-6-7+8-...-99+100
=>B=(1-2-3+4)+(5-6-7+8)-...-(97-98-99+100)
= 0+0-...-0=0
\(B=1-2-3+4+5-6-7+8-...-99+100\)
\(B=\left(1-2-3+4\right)+\left(5-6-7+8\right)-...+\left(97-98-99+100\right)\)
\(B=0+0-...-0\)
\(B=0\)

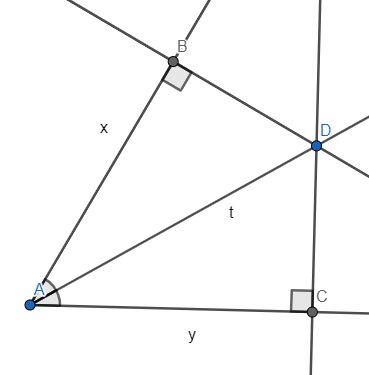
Vì At là tia phân giác của \(\widehat{xAy}\) nên \(\widehat{BAD}=\widehat{CAD}\)
Xét ΔBAD vuông tại B và ΔCAD vuông tại C có:
- AD là cạnh chung
- \(\widehat{BAD}=\widehat{CAD}\) (chứng minh trên)
Suy ra ΔBAD = ΔCAD (cạnh huyền - góc nhọn), từ đó AB = AC (vì hai cạnh tương ứng)


\(-\dfrac{3}{4}.\dfrac{4}{11}+\left(-\dfrac{5}{4}\right).\dfrac{4}{11}=\dfrac{4}{11}\left(-\dfrac{3}{4}-\dfrac{4}{4}\right)=\dfrac{4}{11}.\left(-\dfrac{4}{7}\right)=-\dfrac{16}{77}\)
\(\dfrac{7}{12}-\left(-\dfrac{1}{5}\right)-\dfrac{5}{6}+\dfrac{2}{3}+\left(-\dfrac{1}{5}\right)\)
\(=\dfrac{7}{12}+\dfrac{1}{5}-\dfrac{5}{6}+\dfrac{2}{3}-\dfrac{1}{5}\)
\(=\dfrac{7}{12}-\dfrac{5}{6}+\dfrac{2}{3}=\dfrac{7}{12}-\dfrac{10}{12}+\dfrac{8}{12}=\dfrac{5}{12}\)

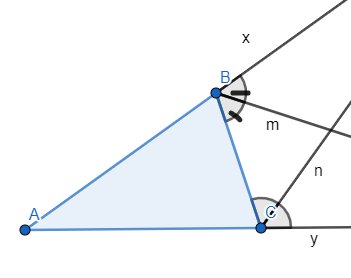
a) Giả sử Bm // Cn. Khi đó ta có:
\(\widehat{xBm}=\widehat{BCn}\) (hai góc đồng vị) và \(\widehat{BCn}+\widehat{CBm}=180^o\) (hai góc trong cùng phía)
\(\Rightarrow\widehat{xBm}+\widehat{mBC}=\widehat{xBC}=180^o\) (a)
Mà \(\widehat{ABC}\) và \(\widehat{xBC}\) là hai góc kề bù (vì \(\widehat{xBC}\) là góc ngoài đỉnh B)
\(\Rightarrow\widehat{ABC}+\widehat{mBC}=180^o\)
\(\Rightarrow\widehat{mBC}=180^o-\widehat{ABC}\)
\(\Rightarrow\widehat{mBC}< 180^o\) (b)
Từ (a) và (b) suy ra vô lí, suy ra Bm không song song với Cn
Vậy Bm cắt Cn

\(18^3< 32^3< 32^9\)
\(\Rightarrow18^3< 32^9\Rightarrow\left(-18\right)^3>\left(-32\right)^9\)
Để so sánh hai số này, chúng ta có thể tính giá trị của mỗi số và so sánh kết quả.
Đầu tiên, tính giá trị của (-32)^9:
(-32)^9 = -134217728
Tiếp theo, tính giá trị của (-18)^3:
(-18)^3 = -5832
Kết quả là (-32)^9 = -134217728 lớn hơn (-18)^3 = -5832.

\(\dfrac{1}{7}\) = 0,(142875)
Mỗi chu kì tuần hoàn của số thập phân có số chữ số là: 6 chữ số.
103 : 6 = 17 dư 1
Vậy chữ số thứ 103 sau dấu phẩy là chữ thứ 1 nhất của chu kỳ thứ:
17 + 1 = 18
Và đó là chữ số 1
Chọn B. 1

A=(x-1)10+(y-3)10+2024.Vì mũ chẵn nên kết quả không thể âm
=>x=0;y=0 và giá trị nhỏ nhất sẽ là:0+0+2024=2024