Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A) \(...=\left(7y-3\right)^3\)
B) \(...=\left(4y-3\right)^3\)
C) \(...=x^4+2x^2+1-\left(y^2+2y+1\right)\)
\(=\left(x^2+1\right)^2-\left(y+1\right)^2\)
D) \(...=x^2-6x+9-\left(y^2-10y+25\right)\)
\(=\left(x-3\right)^2-\left(y-5\right)^2\)

Lời giải:
$3x-2y+6xy=1$
$\Rightarrow (3x+6xy)-(2y+1)=0$
$\Rightarrow 3x(1+2y)-(2y+1)=0$
$\Rightarrow (1+2y)(3x-1)=0$
$\Rightarrow 1+2y=0$ hoặc $3x-1=0$
$\Rightarrow y=\frac{-1}{2}$ hoặc $x=\frac{-1}{3}$ (vô lý vì $x,y$ là số nguyên)
Vậy không tồn tại $x,y$ thỏa mãn đề.

a, -(-12) + (+19) - (+12) + 8 - 19
= 12 + 19 - 12 + 8 - 19
= ( 12 - 12) + ( 19- 19) + 8
= 0 + 0 + 8
= 8
b, (59 - 78) - (42 - 78 + 59)
= 59 - 78 - 42 + 78 - 59
= (59 - 59) - 42 - ( 78 - 78)
= 0 - 42 - 0
= -42
c, ( - 68 + 103) - (-50 - 68 + 103)
= -68 + 103 + 50 + 68 - 103
= (-68 + 68) + ( 103 - 103) + 50
= 0 + 0 + 50
= 50
a) \(...=12+19-12+8-19=8\)
b) \(...=-19-23=-42\)
c) \(...=35-\left(-15\right)=35+15=50\)

`@` `\text {Ans}`
`\downarrow`
\(3^2\cdot2^5\cdot\left(\dfrac{2}{3}\right)^2\)
`=`\(\left(3\cdot\dfrac{2}{3}\right)^2\cdot2^5\)
`=`\(2^2\cdot2^5=2^7\)
\(3^2\cdot2^5\cdot\left(\dfrac{2}{3}\right)^2\)
\(=2^5\cdot\left(3\cdot\dfrac{2}{3}\right)^2\)
\(=2^5\cdot\left(\dfrac{3\cdot2}{3}\right)^2\)
\(=2^5\cdot2^2\)
\(=2^{2+5}\)
\(=2^5\)

Ta có:
`x : y : z = 3 : 8 : 5`
`\Rightarrow `\(\dfrac{x}{3}=\dfrac{y}{8}=\dfrac{z}{5}\)
`\Rightarrow `\(\dfrac{3x}{9}=\dfrac{y}{8}=\dfrac{2z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{3x}{9}=\dfrac{y}{8}=\dfrac{2z}{10}=\dfrac{3x+y-2z}{9+8-10}=\dfrac{14}{7}=2\)
`\Rightarrow`\(\dfrac{x}{3}=\dfrac{y}{8}=\dfrac{z}{5}=2\)
`\Rightarrow`
`x = 3.2 = 6`
`y = 8.2 = 16`
`z = 5.2 = 10`
Vậy, `x = 6; y = 16; z = 10.`

(x+1)7=(x+1)5
=>(x+1)7-(x+1)5=0
=>(x+1)2x(x+1)5-(x+1)5=0
=>(x+1)5x(x+12-1)=0
=>x=0;-1-2
(\(x+1\))7 = (\(x\) + 1)5
(\(x\) + 1)7 - (\(x\) + 1)5 = 0
(\(x\) + 1)5{(\(x\) + 1)2 - 1) = 0
\(\left[{}\begin{matrix}\left(x+1\right)^5=0\\\left(x+1\right)^2-1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x+1=0\\\left(x+1\right)^2=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x+1=1\\x+1=-1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=0\\x=-2\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -2; -1; 0}

a) Ta có: HA = 2RcosA HB = 2RcosB HC = 2RcosC AB = 2RsinC AC = 2RsinB Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2RsinC + 2RsinB Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < sinC + sinB Áp dụng bất đẳng thức tam giác, ta có: sinC + sinB > sin(A + B) = sinCOSA + cosCSINA = cosA + cosB Vậy ta có: cosA + cosB + cosC < sinC + sinB Do đó, ta có HA + HB + HC < AB + AC. b) Ta có: AB + BC + CA = 2R(sinA + sinB + sinC) = 2R(sinA + sinB + sin(A + B)) = 2R(2sin(A + B/2)cos(A - B/2) + sin(A + B)) = 4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B) Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2332 (4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B)) Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) Áp dụng bất đẳng thức tam giác, ta có: sin(A + B) > sinC = sin(A + B/2 + B/2) = sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) Vậy ta có: 2sin(A + B/2)cos(A - B/2) + sin(A + B) < 2sin(A + B/2)cos(A - B/2) + sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + sin(B/2)cos(A + B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2)) Vậy ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) < 1166(sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2))) Do đó, ta có HA + HB + HC < 2332(AB + BC + CA).

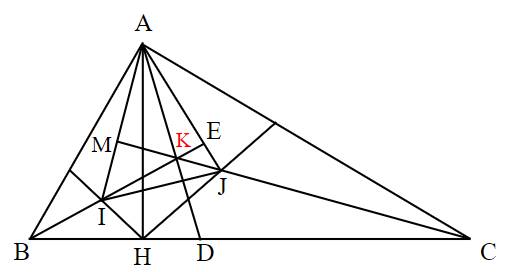
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)
a-3b/2=5a-6b/3
=>a-5a=-6b/3+3b/2
=>-4a=-b/2
Nhân cả 2 vế với -2,ta được:
8a=b
p=a2+32/b2+72
Thay a=8a vào
p=(8a)2+32/(8a)2+72=64a2+9/64a2+49
Vậy kết quả của p là:64a2+9/64a2+49