4/7 x-x = -9/14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
d; \(\dfrac{3}{5}\) : (-5) = \(\dfrac{3}{5}\) x \(\dfrac{1}{\left(-5\right)}\) = \(\dfrac{3}{-25}\) = \(\dfrac{-3}{25}\)
e; \(\dfrac{-4}{15}\): 2 = \(\dfrac{-4}{15}\) x \(\dfrac{1}{2}\) = \(\dfrac{-4}{30}\)
f; 24 : \(\dfrac{-6}{7}\) = 24 x \(\dfrac{7}{-6}\) = \(\dfrac{28}{-1}\) = -28
Bài 3:
b; \(\dfrac{-4}{5}\) : \(\dfrac{2}{7}\) + \(\dfrac{4}{7}\)
= \(\dfrac{-4}{5}.\dfrac{7}{2}\) + \(\dfrac{4}{7}\)
= \(\dfrac{-14}{5}\) + \(\dfrac{4}{7}\)
= \(\dfrac{-98}{35}\) + \(\dfrac{20}{35}\)
= \(\dfrac{-78}{35}\)

\(\dfrac{1}{2}x-\dfrac{3}{5}x=-\dfrac{2}{3}\)
\(x\left(\dfrac{1}{2}-\dfrac{3}{5}\right)=-\dfrac{2}{3}\)
\(\dfrac{1}{10}x=-\dfrac{2}{3}\)
\(x=-\dfrac{20}{3}\)

Lời giải:
Gọi $d=ƯCLN(3n+1, n(3n+2))$
$\Rightarrow 3n+1\vdots d; n(3n+2)\vdots d$
$\Rightarrow n(3n+1)+n\vdots d$
Mà $3n+1\vdots d\Rightarrow n\vdots d$
$\Rightarrow 3n+1-3n\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy ps $\frac{3n+1}{n(3n+2)}$ là phân số tối giản.

\(\dfrac{2}{5}+\dfrac{3}{4}:x=-\dfrac{1}{2}\)
\(\Rightarrow\dfrac{3}{4}:x=-\dfrac{1}{2}-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{3}{4}:x=-\dfrac{9}{10}\)
\(\Rightarrow x=\dfrac{3}{4}:-\dfrac{9}{10}\)
\(\Rightarrow x=-\dfrac{5}{6}\)
Vậy; ...

\(\dfrac{5355}{918}=\dfrac{5355:153}{918:153}=\dfrac{35}{6}\)

\(\dfrac{1}{2}a^2+1=2\)
\(\Rightarrow\dfrac{1}{2}a^2=2-1\)
\(\Rightarrow\dfrac{1}{2}a^2=1\)
\(\Rightarrow a^2=2\)
\(\Rightarrow a^2=\left(\sqrt{2}\right)^2\)
\(\Rightarrow a\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
\(\dfrac{1}{2a^2+1}=2\)
\(2a^2+1=1\)
\(2a^2=0\)
\(a^2=0\)
\(a=0\)

1.2.3.4.5.6.7.8.9 - 1.2.3.4.5.6.7.8 - 1.2.3.4.5.6.7 - 8²
= 1.2.3.4.5.6.7.(8.9 - 8 - 1) - 64
= 5040.63 - 64
= 317520 - 64
= 317456
\(1\times2\times3\times4\times5\times6\times7\times8\times9-1\times2\times3\times4\times5\times6\times7\times8-1\times2\times3\times4\times5\times6\times7-8^2\)
\(=1\times2\times3\times4\times5\times6\times7\times\left(8\times9-8-1\right)-64\)
\(=5040\times63-64\)
\(=317520-64\)
\(=317456\)

Lời giải:
a.
$\frac{1}{a}+\frac{-1}{b}=\frac{1}{a-b}$
$\Rightarrow \frac{b-a}{ab}=\frac{1}{a-b}$
$\Rightarrow (b-a)(a-b)=ab$
$\Rightarrow -(a-b)^2=ab$
Với $a,b\in\mathbb{N}^*$, $ab>0$ còn $-(a-b)^2\leq 0$
Do đó $-(a-b)^2\neq ab$
$\Rightarrow$ không tồn tại $a,b\in\mathbb{N}^*$ thỏa mãn điều kiện đề.
b.
$\frac{5}{2a}=\frac{1}{6}+\frac{b}{3}$
$\frac{15}{6a}=\frac{1+2b}{6}=\frac{a+2ab}{6a}$
$\Rightarrow a+2ab=15$
$\Rightarrow a(1+2b)=15$
Do $a,b$ nguyên nên $a, 1+2b$ nguyên. Mà tích $a(1+2b)=15$ nên xét các TH sau:
TH1: $a=1, 2b+1=15\Rightarrow a=1; b=7$
TH2: $a=-1, 2b+1=-15\Rightarrow a=-1; b=-8$
TH3: $a=15, 2b+1=1\Rightarrow a=15; b=0$
TH4: $a=-15; 2b+1=-1\Rightarrow a=-15; b=-1$
TH5: $a=3, 2b+1=5\Rightarrow a=3; b=2$
TH6: $a=-3, 2b+1=-5\Rightarrow a=-3; b=-3$
TH7: $a=5; 2b+1=3\Rightarrow a=5; b=1$
TH8: $a=-5; 2b+1=-3\Rightarrow a=-5; b=-2$


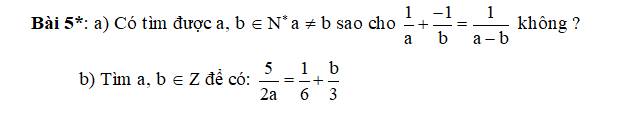 Giúp mình với . Cảm ơn rất nhiều !
Giúp mình với . Cảm ơn rất nhiều !
\(\dfrac{4}{7}x-x=-\dfrac{9}{14}\)
\(\left(\dfrac{4}{7}-1\right)x=-\dfrac{9}{14}\)
\(-\dfrac{3}{7}x=-\dfrac{9}{14}\)
\(x=-\dfrac{9}{14}:\dfrac{-3}{7}\)
\(x=\dfrac{3}{2}\)
\(\dfrac{4}{7}x-x=-\dfrac{9}{14}\)
\(\Rightarrow x\cdot\left(\dfrac{4}{7}-1\right)=-\dfrac{9}{14}\)
\(\Rightarrow x\cdot\dfrac{-3}{7}=\dfrac{-9}{14}\)
\(\Rightarrow x=\dfrac{-9}{14}:\dfrac{-3}{7}\)
\(\Rightarrow x=\dfrac{3}{2}\)
Bạn chỉnh lại môn học nhé.