Mình làm câu 2 trước nhé:

đkxđ: \(\dfrac{1}{2}< x\le2\)

 Áp dụng BĐT Bunyakovsky, ta có \(VT=\left(1.\sqrt{x}+1.\sqrt{2-x}\right)\)\(\le\sqrt{\left(1^2+1^2\right)\left[\left(\sqrt{x}\right)^2+\left(\sqrt{2-x}\right)^2\right]}\) \(=2\). ĐTXR \(\Leftrightarrow x=2-x\Leftrightarrow x=1\) (nhận). Vậy \(VT\le2\)     (1)

 Mặt khác, ta có \(\left(x-1\right)^2\ge0\) \(\Leftrightarrow x^2-\left(2x-1\right)\ge0\) \(\Leftrightarrow\left(x-\sqrt{2x-1}\right)\left(x+\sqrt{2x-1}\right)\ge0\). Do \(x+\sqrt{2x-1}>0\) nên điều này có nghĩa là \(x\ge\sqrt{2x-1}\) \(\Rightarrow\dfrac{x}{\sqrt{2x-1}}\ge1\) \(\Leftrightarrow\dfrac{2x}{\sqrt{2x-1}}\ge2\) hay \(VP\ge2\)  (2). ĐTXR \(\Leftrightarrow x=1\) (nhận)

 Từ (1) và (2) suy ra \(VT\le2\le VP\), do đó pt đã cho \(\Leftrightarrow VT=VP\) \(\Leftrightarrow x=1\) 

 Vậy pt đã cho có nghiệm duy nhất \(x=1\)

Không=))

Lời giải:
Coi số sách ngày đầu Mai đọc là 3 phần thì số sách ngày hai Mai đọc là 4 phần. 

Tổng số phần bằng nhau:

$3+4=7$ (phần) 

Số sách đọc ngày đầu: $238:7\times 3=102$ (trang sách) 

Số sách đọc ngày hai: $238:7\times 4=136$ (trang sách)

Lời giải:

a. Thời gian người đó đi quãng đường AB: 

$90:36=2,5$ (giờ) (=2h30')

b. Người đó đến B lúc:

$9h15'+2h30'+10'=11h55'$

Lời giải:

a. $3\times 15+18:(6+3)=45+18:9=45+2=47$
b. (3\times 15+18):(6+3)=7$

c. $3\times (15+18:6+3)=63$

9 người

9km/h ạ mik ghi nhầm

                                              Bài giải

 Ta có sơ đồ:

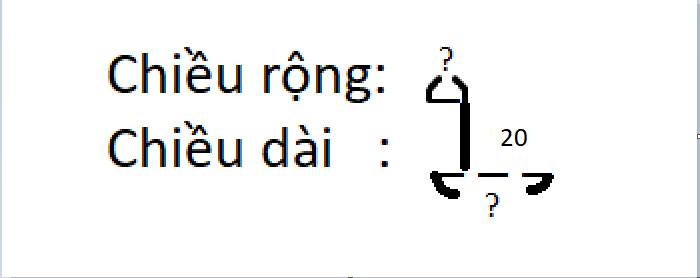
                            Hiệu số phần bằng nhau là:

                                     3 - 1 = 2 ( phần )

                                   Chiều rộng là:

                                  20 : 2 x 3 = 30 ( cm )

                                    Chiều dài là:

                                 20 + 30 = 50 ( cm )

a,                             Diện tích ruộng vườn là:

                                50 x 30 = 1500 ( cm2 )

b,                       1500 cm2 gấp 100m2 số lần là:

                               1500 : 100 = 15 ( lần )

                               Có số yến khoai là:

                                15 x 3 = 45 ( yến )

                             Đổi : 45 yến = 450 kg

                                              Đáp số: a, 1500 cm2

                                                           b,  450 kg

                                Bài giải

                     Vận tốc của ca nô là:

         ( 22,5 + 1,6 ) : 2 = 12,05 ( km/giờ )

                                 Đáp số: 12,05 km/giờ

Vận tốc ca nô xuôi dòng = vận tốc ca nô +vận tốc dòng nước

Vận tốc ca nô khi nước lặng là:

22,5  - 1,6 = 20,9 (km/h)

Đáp số: 20,9 km/h