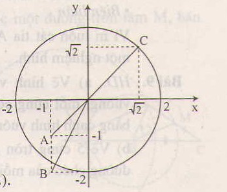
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(-1;-1), B(-1;-2),C(√2;√2)C(2;2) đối với đường tròn tâm O bán kính 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
4 tháng 7 2017
Ta có: \(a^5+b^5\ge a^2b^2\left(a+b\right)\)
\(\Leftrightarrow a^5+b^5+2abc\ge a^2b^2\left(a+b\right)+2abc\)
\(\ge ab\left[ab\left(a+b\right)+2c\right]\ge ab\left[2\left(a+b\right)+2c\right]=2ab\left(a+b+c\right)\) (áp dụng với \(a,b,c\ge\sqrt{2}\))
\(\Rightarrow\frac{1}{a^5+b^5+2abc}\le\frac{1}{2ab\left(a+b+c\right)}\)
Áp dụng vào bài toán ta được
\(P\le\frac{1}{2xy\left(x+y+z\right)}+\frac{1}{2yz\left(x+y+z\right)}+\frac{1}{2zx\left(x+y+z\right)}\)
\(=\frac{x+y+z}{2xyz\left(x+y+z\right)}=\frac{1}{2xyz}\)
TA
3 tháng 7 2017
a ; \(3x-7\sqrt{x}+4=0
\)
\(3x-3\sqrt{x}-4\sqrt{x}+4=0\)\(\left(\sqrt{x}-1\right)\left(3\sqrt{x}-4\right)=0\)
từ đó suy ra x
4 tháng 7 2017
\(a,\frac{2}{3+2\sqrt{2}}-\frac{7}{1-2\sqrt{2}}+\frac{4}{\sqrt{5}-1}+\sqrt{8}-2\)
\(=\frac{2.\left(3-2\sqrt{2}\right)}{9-8}-\frac{7.\left(1+2\sqrt{2}\right)}{1-8}+\frac{4.\left(\sqrt{5}+1\right)}{5-1}+2\sqrt{2}-2\)
\(=6-4\sqrt{2}-\frac{7.\left(1+2\sqrt{2}\right)}{-7}+\frac{4.\left(\sqrt{5}+1\right)}{4}+2\sqrt{2}-2\)
\(=6-4\sqrt{2}+1+2\sqrt{2}+\sqrt{5}+1+2\sqrt{2}-2\)
\(=6+\sqrt{5}\)
\(b,\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{5}}\)
\(=\frac{1-\sqrt{2}}{1-2}+\frac{\sqrt{3}-\sqrt{2}}{3-2}+\frac{\sqrt{4}-\sqrt{5}}{4-5}\)
\(=\frac{1-\sqrt{2}}{-1}+\frac{\sqrt{3}-\sqrt{2}}{1}+\frac{\sqrt{4}-\sqrt{5}}{-1}\)
\(=-1+\sqrt{2}+\sqrt{3}-\sqrt{2}-2+\sqrt{5}\)
\(=-3+\sqrt{3}+\sqrt{5}\)
\(c,\sqrt{4-2\sqrt{3}}+2\sqrt{3}\)
\(=\sqrt{\left(\sqrt{3}-1\right)^2}+2\sqrt{3}\)
\(=\sqrt{3}-1+2\sqrt{3}\)
\(=-1+3\sqrt{3}\)
\(d,A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\)
\(=\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}+\frac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)
\(=\frac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}+\frac{\sqrt{\left(\sqrt{3}+1\right)^2}}{\sqrt{2}}\)
\(=\frac{\sqrt{3}-1}{\sqrt{2}}+\frac{\sqrt{3}+1}{\sqrt{2}}\)
\(=\frac{\sqrt{3}-1+\sqrt{3}+1}{\sqrt{2}}\)
\(=\frac{2\sqrt{3}}{\sqrt{2}}\)
\(=\sqrt{6}\)
\(e,B=\sqrt{\frac{2}{2+\sqrt{3}}}\)
Ta có \(\frac{2}{2+\sqrt{3}}=\frac{2.\left(2-\sqrt{3}\right)}{4-3}=4-2\sqrt{3}\)
Thay lại ta được \(\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}-1\)
.... Đúng thì ủng hộ nha ....
Kết bạn với mình ... ;) ;)
4 tháng 7 2017
\(a,\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-12\sqrt{7}+18+12\sqrt{7}\)
\(=32\)
\(b,\left(3\sqrt{5}+2\sqrt{3}\right).\sqrt{5}-\sqrt{60}\)
\(=15+2\sqrt{15}-2\sqrt{15}\)
\(=15\)
Đúng thì ủng hộ nha ...
Kết bạn với mình .. ;) ;)
KD
0
CH
\(\sqrt{\frac{1}{^{\left(a-b\right)^2}}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}}\)
0
3 tháng 7 2017
Căn thức có nghĩa \(\Leftrightarrow x^2-3\ge0\Rightarrow\sqrt{3}\le x\le-\sqrt{3}\)
\(\Leftrightarrow x^2-2x-3\ge0\)
\(\Leftrightarrow x\left(x+2\right)\ge0\)
\(\Leftrightarrow x^2+5x+6\ge0\)
SL
3 tháng 7 2017
Bạn tìm điều kiện để cái trong căn lớn hơn bằng 0 la ok luôn mà
LA
3 tháng 7 2017
Ta có a² + \(\sqrt{a}\) + \(\sqrt{a}\) ≥ 3a ( 1 )
b² + \(\sqrt{b}\) + \(\sqrt{b}\) ≥ 3b ( 2 )
c² + \(\sqrt{c}\) + \(\sqrt{c}\) ≥ 3c ( 3 )
Cộng từng vế ( 1 ) ( 2 ) ( 3 ) cho ta
a² + b² + c² + 2 ( \(\sqrt{a}+\sqrt{b}+\sqrt{c}\) ) ≥ 3 ( a + b + c ) = 9
2 ( \(\sqrt{a}+\sqrt{b}+\sqrt{c}\)) ≥ 9 - ( a² + b² + c² )
2 ( \(\sqrt{a}+\sqrt{b}+\sqrt{c}\) ) ≥ 9 - ( a + b + c )² + 2 (ab + bc + ca) = 2 (ab + bc + ca)
Vậy\(\sqrt{a}+\sqrt{b}+\sqrt{c}\) ≥ ab + bc + ca
Dấu bằng xãy ra khi và chỉ khi a = b = c = 1
Vậy......
Khoảng cách d từ gốc tọa độ đến điểm (x;y) được tính theo công thức d=√x2+y2d=x2+y2
Ta có OA=√2<2⇒AOA=2<2⇒A nằm trong đường tròn (O;2).
OB=√5>2⇒BOB=5>2⇒B nằm ngoài đường tròn (O;2).
OC=2⇒COC=2⇒C nằm trên đường tròn (O;2).