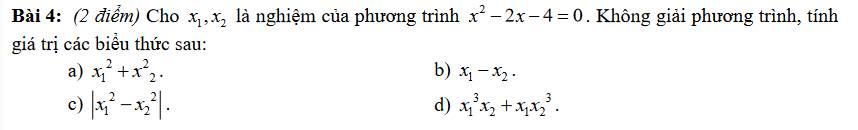
giúp mik câu b,c,d với :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x_1+x_2=-\dfrac{b}{a}=-5;x_1x_2=2\)
\(x_1^2\cdot x_2^3+x_2^2\cdot x_1^3\)
\(=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)\)
\(=2^2\cdot\left(-5\right)=-20\)

Pt: \(x^2+5x+2=0\)
Theo vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-5}{1}=-5\\x_1x_2=\dfrac{2}{1}=2\end{matrix}\right.\)
a) \(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2\cdot2=25-4=21\)
b) \(x_1^3+x_2^3=\left(x_1+x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\right]\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=\left(-5\right)\cdot\left[\left(-5\right)^2-3\cdot2\right]=-95\)
c) \(\left|x_1-x_2\right|=\sqrt{\left|x_1-x_2\right|^2}=\sqrt{x_1^2+x_2^2-2\left|x_1x_2\right|}\)
\(=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|}=\sqrt{\left(-5\right)^2-2\cdot2-2\cdot\left|2\right|}=\sqrt{17}\)
d) \(x_1^2x_2^3+x_2^2x_1^3=x_1^2x_2^2\left(x_1+x_2\right)=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)=2^2\cdot\left(-5\right)=-20\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=2\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2.2=21\)
\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(-5\right)^3-3.2.\left(-5\right)=-95\)
\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-5\right)^2-4.2}=\sqrt{17}\)
\(x_1^2x_2^3+x_1^3x_2^2=\left(x_1x_2\right)^2\left(x_1+x_2\right)=2^2.\left(-5\right)=-20\)

+ Đông Nam Bộ:
--> Đông Nam Bộ có địa hình chủ yếu là đồi núi thấp và thoải.
--> Chủ yếu là đất xám, đất ba dan thích hợp trồng cây công nghiệp như cà phê, hồ tiêu, mía đường, thuốc lá, hoa quả.
--> Thuộc loại cận xích đạo gió mùa, nóng ẩm quanh năm thích hợp cho việc trồng trọt cả 4 mùa.
--> Sông Đồng Nai có giá trị về thủy điện đồng thời cung cấp nguồn nước cho sản xuất và sinh hoạt của con người.
--> Tuy rừng không nhiều nhưng là nơi đảm bảo sự sống cho sinh thủy ở các sông và là địa điểm du lịch thú vị.
--> Nhiều thủy, hải sản, biển ấm và ngư trường rộng, đặc biệt gần đường hàng hải quốc tế thuận lợi cho khai thác thủy hải sản, dầu khí, giao thông vận tải và du lịch.
+ Đồng Bằng Sông Cửu Long:
--> Đồng bằng rộng lớn, diện tích khoảng 4 triệu ha và khá bằng phẳng.
--> Đất có 3 loại (phù sa ngọt, đất phèn và đất mặn). Trong đó, đất phù sa ngọt có độ màu mỡ cao thuận lợi để thâm canh lúa nước.
--> Cận xích đạo gió mùa nóng ẩm quanh năm, lượng mưa dồi dào.
--> Sông Mê Công đem lại nguồn lợi lớn về phù sa và thuỷ sản, hệ thống kênh rạch chằng chịt thuận lợi giao thông thuỷ bộ và nuôi thuỷ sản nước ngọt, sinh vật phong phú, đa dạng.


Gọi thời gian đi từ A đến B là x(giờ)
(ĐK: x>0)
Thời gian đi từ B đến C là x+0,5(giờ)
Độ dài quãng đường từ A đến B là 10x(km)
Độ dài quãng đường từ B đến C là 9(x+0,5)(km)
Độ dài AC là 33km nên ta có:
10x+9(x+0,5)=33
=>19x+4,5=33
=>19x=33-4,5=30-1,5=28,5
=>x=1,5(nhận)
vậy: Thời gian đi từ A đến B là 1,5 giờ
Thời gian đi từ B đến C là 1,5+0,5=2 giờ

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp đường tròn đường kính OA
tâm là trung điểm của OA
b: Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{ABD}=\widehat{BED}\)
mà \(\widehat{BED}=\widehat{DAK}\)(hai góc so le trong, BE//AC)
nên \(\widehat{KAD}=\widehat{KBA}\)
Xét ΔKAD và ΔKBA có
\(\widehat{KAD}=\widehat{KBA}\)
\(\widehat{AKD}\) chung
Do đó: ΔKAD~ΔKBA
=>\(\dfrac{KA}{KB}=\dfrac{KD}{KA}\)
=>\(KA^2=KB\cdot KD\)
Xét (O) có
\(\widehat{KCD}\) là góc tạo bởi tiếp tuyến CK và dây cung CD
\(\widehat{CBD}\) là góc nội tiếp chắn cung CD
Do đó: \(\widehat{KCD}=\widehat{CBD}\)
Xét ΔKCD và ΔKBC có
\(\widehat{KCD}=\widehat{KBC}\)
\(\widehat{CKD}\) chung
Do đó: ΔKCD~ΔKBC
=>\(\dfrac{KC}{KB}=\dfrac{KD}{KC}\)
=>\(KC^2=KB\cdot KD\)
=>KC=KA
=>K là trung điểm của AC

a: Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{ACB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}=45^0\)
Xét tứ giác ANMB có \(\widehat{ANB}=\widehat{AMB}=90^0\)
nên ANMB là tứ giác nội tiếp
b: Xét (O) có \(\widehat{BNA}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung BA và CE
=>\(\widehat{BNA}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CE}\right)\)
=>\(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CE}=90^0\cdot2=180^0\)
=>\(sđ\stackrel\frown{CE}=90^0\)
Xét (O) có \(\widehat{BMA}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung BA và DC
=>\(\widehat{BMA}=\dfrac{1}{2}\left(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CD}\right)\)
=>\(sđ\stackrel\frown{CD}+90^0=2\cdot\widehat{BMA}=180^0\)
=>\(sđ\stackrel\frown{CD}=90^0\)
\(sđ\stackrel\frown{ED}=sđ\stackrel\frown{CD}+sđ\stackrel\frown{DE}=90^0+90^0=180^0\)
=>E,O,D thẳng hàng
=>DE là đường kính của (O)
Xét (O) có
ΔDAE nội tiếp
DE là đường kính
Do đó; ΔDAE vuông tại A
=>DA\(\perp\)IE tại A
mà DA\(\perp\)BC
nên BC//IA
Xét (O) có
ΔDBE nội tiếp
DE là đường kính
Do đó: ΔDBE vuông tại C
=>DB\(\perp\)BE
mà BE\(\perp\)CA
nên DB//CA
Xét tứ giác ACBI có
AC//BI
AI//BC
Do đó: ACBI là hình bình hành

Gọi chiều dài của mảnh vườn là: \(x\left(m\right)\)
chiều rộng của mảnh vườn là: \(y\left(m\right)\)
ĐK: \(x,y>0\)
Chu vi của mảnh vườn là 130m ta có:
\(\left(x+y\right)\cdot2=130\Leftrightarrow x+y=\dfrac{130}{2}=65\left(1\right)\)
Hai lần chiều dài hơn ba lần chiều rộng 35m nên ta có:
\(2x-3y=35\left(2\right)\)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}x+y=65\\2x-3y=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=130\\2x-3y=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=95\\x+y=65\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=19\\x=65-19=46\end{matrix}\right.\left(tm\right)\)
Diện tích của mảnh vườn là: \(19\cdot46=874\left(m^2\right)\)
a: Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=2;x_1x_2=-4\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=2^2-2\cdot\left(-4\right)=4+8=12\)
b: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=2^2-4\cdot\left(-4\right)=20\)
=>\(x_1-x_2=\pm2\sqrt{5}\)
c: \(\left|x_1^2-x_2^2\right|\)
\(=\left|\left(x_1-x_2\right)\left(x_1+x_2\right)\right|\)
\(=\left|2\sqrt{5}\cdot2\right|=4\sqrt{5}\)
d: \(x_1^3\cdot x_2+x_1\cdot x_2^3\)
\(=x_1x_2\left(x_1^2+x_2^2\right)\)
\(=-4\cdot12=-48\)