Cho 𝛥𝐴𝐵𝐶 cân tại A, B=47o ; Gọi M là trung điểm của BC.
a) Tính số đo các góc của tam giác ABC
b) Chứng minh : 𝛥𝐴𝐵𝑀 = 𝛥𝐴𝐶𝑀
c) Chứng minh : AM + BM > AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot15=10\left(cm\right)\)
b: Xét ΔABM và ΔCEM có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MB=ME
Do đó: ΔMAB=ΔMCE
=>\(\widehat{MAB}=\widehat{MCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BA//CE
d: Xét ΔNBF và ΔNAC có
\(\widehat{NBF}=\widehat{NAC}\)(BF//AC)
NB=NA
\(\widehat{BNF}=\widehat{ANC}\)(hai góc đối đỉnh)
Do đó: ΔNBF=ΔNAC
=>NF=NC
Xét ΔNAF và ΔNBC có
NA=NB
\(\widehat{ANF}=\widehat{BNC}\)(hai góc đối đỉnh)
NF=NC
Do đó: ΔNAF=ΔNBC
=>AF=BC
ΔNAF=ΔNBC
=>\(\widehat{NAF}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
Xét ΔMAE và ΔMCB có
MA=MC
\(\widehat{AME}=\widehat{CMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMCB
=>AE=CB
ΔMAE=ΔMCB
=>\(\widehat{MAE}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF(=BC)
nên A là trung điểm của EF


\(D=-16x^5-28x^4+16x^3-20x^2+32x+2016\)
\(=4x\left(-4x^4-7x^3+4x^2-5x+8\right)+2016\)
\(=4x\cdot0+2016=2016\)

a: A(x)+B(x)
\(=-3x^3+5x^2+4x+1+3x^3+6x^2-8x+9\)
\(=11x^2-4x+10\)
A(x)-B(x)
\(=-3x^3+5x^2+4x+1-3x^3-6x^2+8x-9\)
\(=-6x^3-x^2+12x-8\)
b: C(x)+D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}+4x^3-5x^2-3x-\dfrac{1}{4}\)
\(=3x^3+2x-1\)
C(x)-D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}-4x^3+5x^2+3x+\dfrac{1}{4}\)
\(=-5x^3+10x^2+8x-\dfrac{1}{2}\)
c: E(x)+F(x)
\(=3x^3+7x^2+5x-8+3x^3+7x^2-9x+1\)
\(=6x^3+14x^2-4x-7\)
E(x)-F(x)
\(=3x^3+7x^2+5x-8-3x^3-7x^2+9x-1\)
\(=14x-9\)
d: G(x)+H(x)
\(=5x^4-6x^3-3x^2-2x+8+x^4+3x^2-3x-5\)
\(=6x^4-6x^3-5x+3\)
G(x)-H(x)
\(=5x^4-6x^3-3x^2-2x+8-x^4-3x^2+3x+5\)
\(=4x^4-6x^3-6x^2+x+13\)
e: I(x)+J(x)
\(=5x^4-2x^3-6x^2+7x+6+2x^3+3x^2-7x-5\)
\(=5x^4-3x^2+1\)
I(x)-J(x)
\(=5x^4-2x^3-6x^2+7x+6-2x^3-3x^2+7x+5\)
\(=5x^4-4x^3-9x^2+14x+11\)
f: K(x)+L(x)
\(=4x^4+3x^3+5x^2-2x+6-4x^4-3x^3-4x^2+2x-9\)
\(=x^2-3\)
K(x)-L(x)
\(=4x^4+3x^3+5x^2-2x+6+4x^4+3x^3+4x^2-2x+9\)
\(=8x^4+6x^3+9x^2-4x+15\)
g: M(x)+N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19+6x^4-4x^3+3x^2+\dfrac{1}{2}x-20\)
\(=x^4-2x^2-39\)
M(x)-N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19-6x^4+4x^3-3x^2-\dfrac{1}{2}x+20\)
\(=-11x^4+8x^3-8x^2-x+1\)
h:
\(O\left(x\right)=x^5+x^3-4x-x^5+3x+7\)
\(=\left(x^5-x^5\right)+x^3+\left(-4x+3x\right)+7\)
\(=x^3-x+7\)
\(P\left(x\right)=3x^2-x^3+8x-3x^2-14\)
\(=-x^3+\left(3x^2-3x^2\right)+8x-14=-x^3+8x-14\)
O(x)+P(x)
\(=x^3-x+7-x^3+8x-14\)
\(=7x-7\)
O(x)-P(x)
\(=x^3-x+7+x^3-8x+14\)
\(=2x^3-9x+21\)

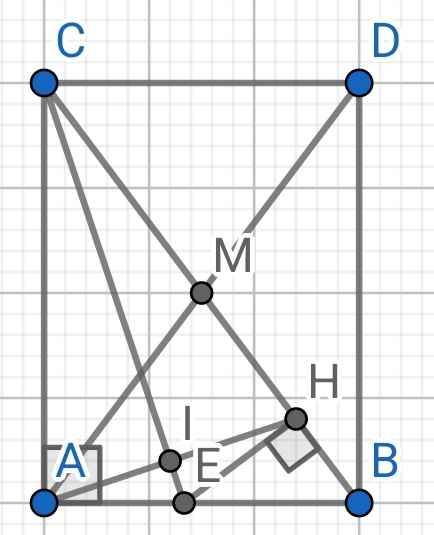
a) ∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠BCA = 90⁰ (hai góc nhọn trong tam giác vuông phụ nhau)
b) Do CE là đường phân giác của ∆ABC (gt)
⇒ CE là tia phân giác của ∠ACB
⇒ ∠ACE = ∠BCE
⇒ ∠ACE = ∠HCE
Xét hai tam giác vuông: ∆ACE và ∆HCE có:
CE là cạnh chung
∠ACE = ∠HCE (cmt)
⇒ ∆ACE = ∆HCE (cạnh huyền - góc nhọn)
⇒ AC = HC (hai cạnh tương ứng)
c) Do ∆ACE = ∆HCE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
⇒ E nằm trên đường trung trực của AH (1)
Do AC = HC (cmt)
⇒ C nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ CE là đường trung trực của AH
Mà I là giao điểm của AH và CE (gt)
⇒ I là trung điểm của AH
⇒ IA = IH
d) Trên tia đối của tia MA lấy điểm D sao cho AM = DM
⇒ M là trung điểm của AD
Do M là trung điểm của BC (gt)
⇒ BM = CM
Xét ∆ABM và ∆DCM có:
AM = DM
∠AMB = ∠DMC (đối đỉnh)
BM = CM (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
⇒ ∠BAM = ∠CDM (hai góc tương ứng)
Mà ∠BAM và ∠CDM là hai góc so le trong
⇒ AB // CD
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ CD ⊥ AC
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABD và ∆CDB có:
AB = CD (cmt)
DB là cạnh chung
⇒ ∆ABD = ∆CDB (hai cạnh góc vuông)
⇒ AD = BC (hai cạnh tương ứng)
Mà M là trung điểm của AD (cmt)
⇒ AD = 2AM
⇒ BC = 2AM


Gọi số quyển sách của An,Bình, Cường lần lượt là a(quyển),b(quyển),c(quyển)
(ĐK: \(a,b,c\in Z^+\))
Số sách của An,Bình,Cường lần lượt tỉ lệ với 3;4;5 nên \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Số sách của Bình ít hơn tổng quyển sách của An và Cường là 8 quyển nên a+c-b=8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+c-b}{3+5-4}=\dfrac{8}{4}=2\)
=>a=3*2=6; b=2*4=8; c=2*5=10
vậy: số quyển sách của An,Bình, Cường lần lượt là 6 quyển; 8 quyển; 10 quyển

Giải
a; Gọi giá tiền của cây thước là y (đồng)
Số tiền còn lại của Lan sau khi mua là
200 000 - y - 2y = 200 000 - 3y (đồng)
b; Số tiền còn lại của Lan sau khi mua một cây thước là:
200 000 - y
Số bút mà Lan có thể mua là:
\(\dfrac{200000-y}{2y}\)

Bài 1:
M(\(x\)) = 3\(x^{3^{ }}\) - \(x^2\) + 3 + 2\(x^3\)
N(\(x\)) = - 2\(x^3\) - \(x\) + \(x^2\) + 3
M(\(x\)) + N(\(x\)) = 3\(x^3\) - \(x^2\) + 3 + 2\(x^3\) - 2\(x^3\) - \(x\) + \(x^2\) + 3
M(\(x\)) + N(\(x\)) = (3\(x^3\) + 2\(x^3\) - 2\(x^3\)) - (\(x^2\) - \(x^2\)) - \(x\) + (3 + 3)
M(\(x\)) + N(\(x\)) = 3\(x^3\) - \(x\) + 6
Bài 2:
a = \(\dfrac{x-2}{3x+1}\) - \(\dfrac{x}{5}\)
Thay \(x\) = - 5 vào biểu thức a ta có:
a = \(\dfrac{-5-2}{3.\left(-5\right)+1}\) - \(\dfrac{-5}{5}\)
a = \(\dfrac{-7}{-14}\) + 1
a = \(\dfrac{1}{2}+1\)
a = \(\dfrac{3}{2}\)
a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=47^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot47^0=86^0\)
b: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
c Xét ΔAMB có AM+BM>AB
mà AB=AC(ΔABC cân tại A)
nên AM+BM>AC