Tìm x sao cho giá trị biểu thức -3x nhỏ hơn giá trị biểu thức -7x+5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vì (a-1)2 ≥ 0 nên a2 +1 ≥ 2a ∀mọi x (1)
vì (b-1)2 ≥ 0 nên b2 +1 ≥ 2b ∀ mọi x (2)
từ 1 và 2 ⇒ a2+b2 ≥ 2a+2b
⇒ A≥ 2(a+b)=2
dấu''=' xảy ra khi a=b=1/2

a/
Xét tg vuông ABC và tg vuông HBA có \(\widehat{ACB}=\widehat{HAB}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg ABC đồng dạng với tg HBA (g.g.g)
b/
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=5\sqrt{5}\) (Pitago)
\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông băng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{81}{5\sqrt{5}}=\dfrac{81\sqrt{5}}{25}\)
\(\Rightarrow CH=BC-BH=5\sqrt{5}-\dfrac{81\sqrt{5}}{25}=\dfrac{44\sqrt{5}}{25}\)
Ta có
\(AH^2=BH.CH\) (trong tg vuông bình phường đường cao thuộc cạnh huyền băng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH^2=\dfrac{81\sqrt{5}}{25}.\dfrac{44\sqrt{5}}{25}\) Khai căn ra AH
c/
Xét tg vuông BHI và tg vuông BEC có \(\widehat{CBE}\) chung
=> tg BHI đồng dạng với tg BEC (g.g.g)
\(\Rightarrow\dfrac{BI}{BC}=\dfrac{BH}{BE}\Rightarrow BI.BE=BH.BC\left(dpcm\right)\)


a) \(\left|x^2-x+2\right|=3x+7\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+2=3x+7\left(ĐK:x\ge-\dfrac{7}{3}\right)\\-x^2+x-2=3x+7\left(ĐK:x\le-\dfrac{7}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x-3x+2-7=0\\-x^2+x-3x+2-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-4x-5=0\\-x^2-2x-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x-5x-5=0\\-\left(x^2+2x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\left(x+1\right)-5\left(x+1\right)=0\\-\left(x^2+2x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)\left(x-5\right)=0\\-\left(x^2+2x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\text{ hoặc }x-5=0\\-\left(x^2+2x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\text{ hoặc }x=5\\\left(-x^2+2x+5\right)=0\left(\text{Vô lý}\right)\end{matrix}\right.\)

Vì \(x^2+1\ne0\) nên ta có thể viết lại:
\(\left(x^2+1\right)Q=2x^2+2x+2\Leftrightarrow Qx^2+Q=2x^2+2x+2\)\(\Leftrightarrow Qx^2-2x^2-2x+Q-2=0\Leftrightarrow\left(Q-2\right)x^2-2x+Q-2=0\) (*)
pt (*) có nghiệm khi \(\Delta'=\left(-1\right)^2-\left(Q-2\right)\left(Q-2\right)=1-\left(Q-2\right)^2\ge0\)\(\Leftrightarrow\left(Q-2\right)^2\le1\)\(\Leftrightarrow-1\le Q-2\le1\)\(\Leftrightarrow1\le Q\le3\) (đpcm)

\(a,\)
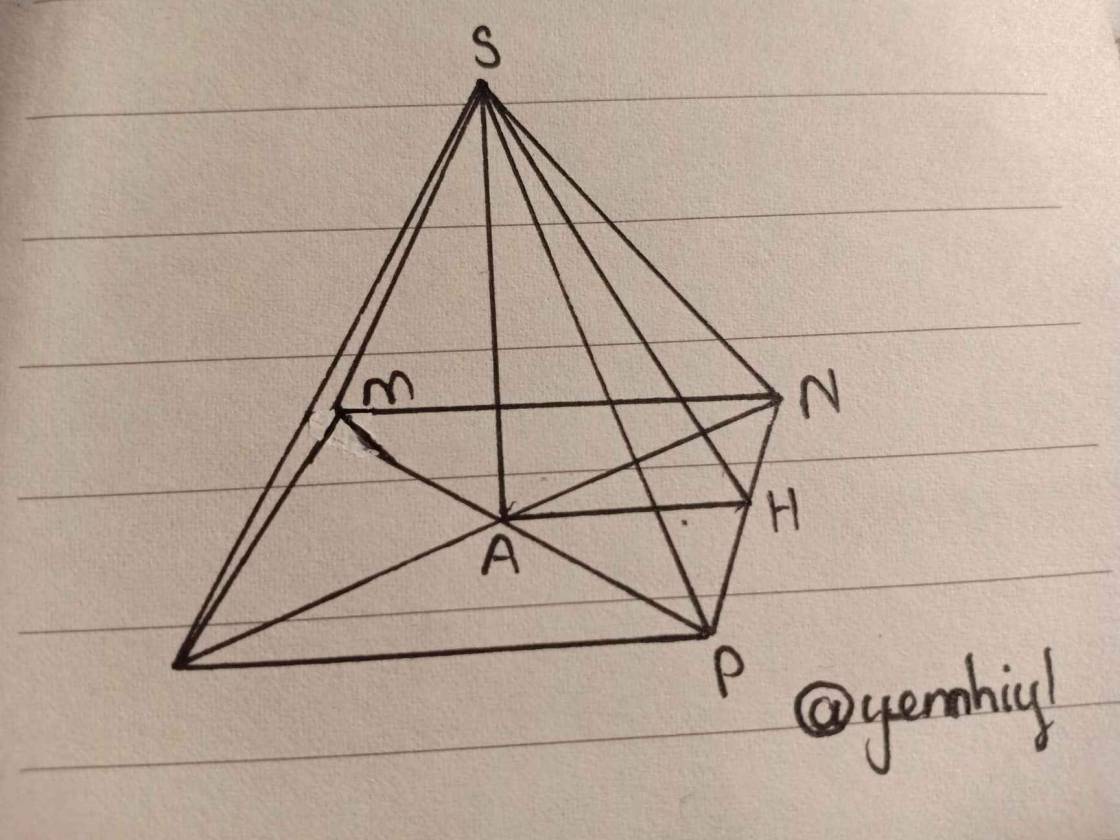
Lều có dạng hình chóp tứ giác đều có chiều cao SA
\(\rightarrow\) Đỉnh hình chóp là S, A là tâm của đáy (đáy là hình vuông)
Gọi đáy là hình vuông MNPQ
\(\rightarrow A\) là giao điểm của MP, NQ
Bán kính đường tròn ngoại tiếp đáy là 6cm
\(\rightarrow AM=AN=AP=AQ=6cm\)
\(\rightarrow MP=NQ=2.6=12cm\)
\(S_{MNPQ}=\dfrac{1}{2}.MP.NQ=\dfrac{1}{2}.12.12=72cm^2\)
Vậy thể tích không khí trong lều là:
\(V=\dfrac{1}{3}.S_{MNPQ}.SA=\dfrac{1}{3}.72.9=216cm^3\)
\(b,\)
Kẻ trung đoạn SH của mặt bên SPN \(\rightarrow\) H là trung điểm PN
\(\Delta ANP\) vuông ở A \(\rightarrow NP^2=AN^2+AP^2\rightarrow NP^2=6^2+6^2\rightarrow NP=6\sqrt{2}cm\)
Ta có: AH là đường trung tuyến \(\rightarrow AH=\dfrac{1}{2}.NP=\dfrac{1}{2}.6\sqrt{2}=3\sqrt{2}cm\)
\(\Delta SAH\) vuông ở A \(\rightarrow SH^2=AH^2+SA^2\rightarrow SH^2=\left(3\sqrt{2}\right)^2+9^2\rightarrow SH=3\sqrt{11}cm\)
\(P_{MNPQ}=C_{MNPQ}=4.NP=4.6\sqrt{2}=24\sqrt{2}cm\)
Vậy số vải bạt cần dùng để dựng chiếc trại đó là:
\(S_{xq}=\dfrac{1}{2}.C_{MNPQ}.SH=\dfrac{1}{2}.24\sqrt{2}.3\sqrt{11}=36\sqrt{22}cm^2\)
 có ai làm dc ko giúp mình
có ai làm dc ko giúp mình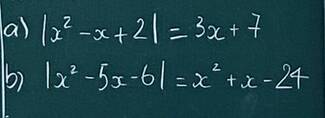
-3x < -7x+5 <=> 4x<5 <=>x<5/4 vậy x < 5/4 để giá trị BT -3x nhỏ hơn giá trị BT -7x+5
-3x<-7x+5
<=>-3x+7x<5
<=>4x<5
<=>x<5/4
xin 1 tick nhé