0 

7197x547x0

=7197x(547x0)

=7197x0

=0

\(y=\dfrac{x^2-3x+1}{x-2}\)

\(D=R\ne\left\{2\right\}\)

\(\lim\limits_{x\rightarrow2^+}y=\dfrac{-1}{0^+}=-\infty\)

Vậy TCĐ của HS là: x=2

Hoặc cách khác: 

Xét mẫu bằng 0 với giá trị đó nếu tử khác 0 => Là TCĐ

nếu tử bằng 0 => HS không có TCĐ

.

\(y=\dfrac{x^2-3x+1}{x-2}=\dfrac{x\left(x-2\right)-\left(x-2\right)-1}{x-2}=x-1-\dfrac{1}{x-2}\)

Ta thấy: \(\lim\limits_{x\rightarrow+\infty}\left[y-\left(x-1\right)\right]=\lim\limits_{x\rightarrow+\infty}-\dfrac{1}{x-2}=0\)

Vậy: y=x-1 là TCX của HS

6777

Lớp 1 ? 

Diện tích hình tròn là:

   \(3,14\times25\times25:4=490,625\left(cm^2\right)\)

          Đáp số: \(490,625cm^2\)

Bán kính hình tròn đó là :

\(25\div2=12,5\left(cm\right)\)

S hình tròn đó là :

\(12,5\times12,5\times3,14=490,625\left(cm^2\right)\)

          bài làm

Tổng số phần bằng nhau là: 

5 + 3 = 8 (phần)

Một cái bút có giá:

72 : 8 x 3 = 27000 (đồng)

d/s

Giá tiền của 1 quyển truyện là :

\(72000\div\left(5+3\right)\times5=45000\left(\text{đ}\text{ồng}\right)\)

Giá tiền của 1 cái bút là :

\(72000-45000=27000\left(\text{đ}\text{ồng}\right)\)

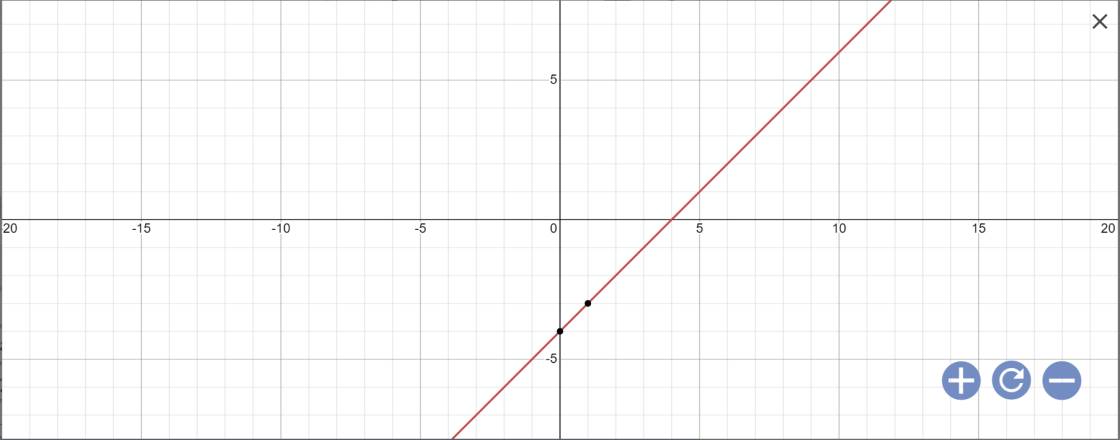
x-y=4

=>y=x-4

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=x-4\end{matrix}\right.\)

Biểu diễn nghiệm:

X x 123 = 322 + 776

X x 123 = 1098

X = 1098 : 123

X = 1098/123

Chú ý lần sau không ghi nội dung không liên quan đến bài tập bạn nhé

\(X\times123=322+766\\ \text{X}\times123=1088\\ \text{X}=1=1088\div123\\ \text{X}=\dfrac{1088}{123}\)

a: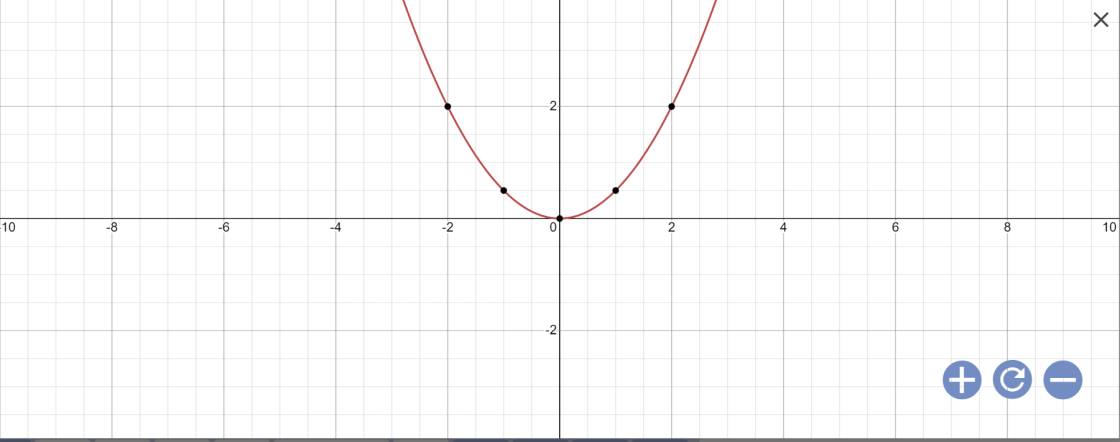 

b: Thay x=0 và y=-2 vào (d1), ta được:

\(a\cdot0+b=-2\)

=>b=-2

=>(d1): y=ax-2

Thay x=1 và y=3 vào (d1), ta được:

\(a\cdot1-2=3\)

=>a-2=3

=>a=5

Vậy: (d1): y=5x-2

c: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=2x+m\)

=>\(x^2=4x+2m\)

=>\(x^2-4x-2m=0\)

\(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(-2m\right)=8m+16\)

Để (P) cắt (d2) tại hai điểm phân biệt thì 8m+16>0

=>8m>-16

=>m>-2

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-2m\end{matrix}\right.\)

\(x_1+x_2-2x_1x_2=2024\)

=>\(4-2\cdot\left(-2m\right)=2024\)

=>4m+4=2024

=>m+1=506

=>m=505(nhận)

Quãng đường anh ta đi dài:

\(13234\times2=26468\left(m\right)\)

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\)

\(\Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]-105=0\)

\(\Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)-105=0\) (1)

Đặt \(x^2+10x+20=t\), khi đó (1) trở thành:

\(\left(t-4\right)\left(t+4\right)-105=0\)

\(\Leftrightarrow t^2-16-105=0\)

\(\Leftrightarrow t^2-11^2=0\)

\(\Leftrightarrow\left(t-11\right)\left(t+11\right)=0\)

\(\Rightarrow\left(x^2+10x+20-11\right)\left(x^2+10x+20+11\right)=0\)

\(\Leftrightarrow\left(x^2+10x+9\right)\left(x^2+10x+31\right)=0\)

\(\Leftrightarrow\left(x^2+9x+x+9\right)\left[\left(x+5\right)^2+6\right]=0\)

\(\Leftrightarrow x\left(x+9\right)+\left(x+9\right)=0\) (vì \(\left(x+5\right)^2+6>0;\forall x\))

\(\Leftrightarrow\left(x+9\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+9=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=-1\end{matrix}\right.\)

Vậy phương trình đã cho có tập nghiệm là $S=\{-9;-1\}$.

$Toru$

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\\ \Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]=105\\ \Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)=105\\ \Leftrightarrow\left(x^2+10x+20-4\right)\left(x^2+10x+20+4\right)=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2-4^2=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2=121\\ \)

\(\Rightarrow\left[{}\begin{matrix}x^2+10x+20=11\left(1\right)\\x^2+10x+20=-11\left(2\right)\end{matrix}\right.\)

Giải (1):

\(x^2+10x+9=0\\ \Leftrightarrow\left(x^2+x\right)+\left(9x+9\right)=0\\ \Leftrightarrow x\left(x+1\right)+9\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-9\end{matrix}\right.\)

Giải (2):

Nhận thấy: \(x^2+10x+20=\left(x+5\right)^2-5\ge-5\forall x\inℝ\)

Vậy pt (2) vô nghiệm

Vậy tập nghiệm pt là: \(S=\left\{-1;-9\right\}\)