Ta có: \(1=a^2+b^2+c^2\ge ab+bc+ca\).

\(P=\dfrac{a^3}{b+2c}+\dfrac{b^3}{c+2a}+\dfrac{c^3}{a+2b}=\dfrac{a^4}{ab+2ca}+\dfrac{b^4}{bc+2ab}+\dfrac{c^4}{ca+2bc}\)

\(\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{3\left(ab+bc+ca\right)}=\dfrac{1}{3\left(ab+bc+ca\right)}\ge\dfrac{1}{3}\)

Dấu \(=\) xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\).

Thể tích của bể là: 25 x 15 x 22 = 8250 (cm³)

Đổi: 1L = 1 dm³; 8250 cm³ = 8,25 dm³

Thể tích của nước là: 1 x 7 = 7 (L)

Vì 7 < 8,25 nên khi cho 7 lít nước vào thì vẫn chưa đấy bể.

không đầy bể

ko bt

\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)

\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)

\(\Leftrightarrow2x^3-6x^2-6x-8=0\)

\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)

\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)

\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)

Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)

\(\Rightarrow x-4=0\Leftrightarrow x=4\)

Lời giải:
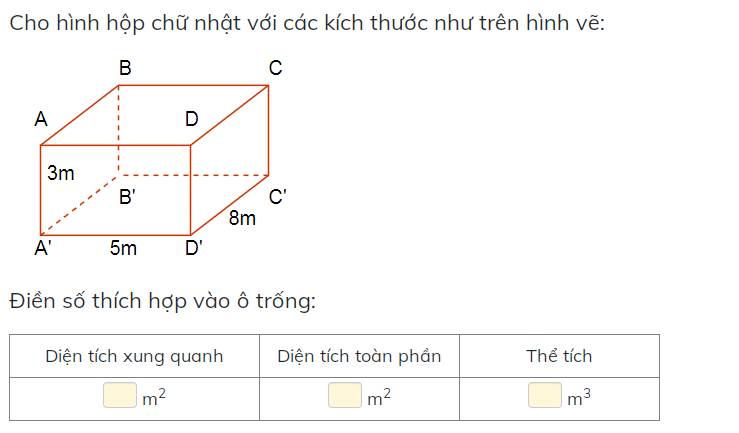
Diện tích xung quanh: $2(3.5+3.8)=78$ (m²)

Diện tích toàn phần: $78+2.5.8=158$ (m²)

Thể tích: $3\times 5\times 8=120$ (m³)

Diện tích xung quanh là 78 m\(^2\).

Diện tích toàn phần là 158 m\(^2\).

Thể tích là 120 m\(^3\).

Điều kiện: \(x\ne1\)

\(\Leftrightarrow\dfrac{2}{x-1}-1>0\)

\(\Leftrightarrow\dfrac{2-x+1}{x-1}>0\)

\(\Leftrightarrow\dfrac{3-x}{x-1}>0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-x>0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-x< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 3\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x>3\\x< 1\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow1< x< 3\)