bạn nhớ vote cho mình nhaa

a) Vì tam giác ABC cân tại A nên ta có:

Góc BAC = Góc BCA = 47^o
Góc ABC = 180o - 2 x 47^o = 86^o
b) Ta có:

AB = AC (do tam giác ABC cân tại A)
BM = MC (do M là trung điểm của BC)
∠ABM = ∠ACM = 90^o - 47^o = 43^o (do ∠BAC = 47^o và ∠BAM, ∠CAM là góc vuông) 
Vậy, 𝛥𝐴𝐵𝑀 = 𝛥𝐴𝐶𝑀 (theo định lý tam giác cân)
c) Ta có:

AM + BM = AB + BM (do AB = AM)
AB + BM > AC (do tổng độ dài hai cạnh của một tam giác luôn lớn hơn cạnh còn lại) 
Vậy, AM + BM > AC

a: Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

b: Ta có: ΔBAD=ΔBED

=>DA=DE

Ta có: ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}=90^0\)

=>DE\(\perp\)BC tại E

Xét ΔDAK vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó; ΔDAK=ΔDEC

=>AK=EC

c: Ta có; ΔDAK=ΔDEC

=>DK=DC 

=>D nằm trên đường trung trực của KC(1)

Ta có: IK=IC

=>I nằm trên đường trung trực của KC(2)

Ta có: BA+AK=BK

BE+EC=BC
mà BA=BE và AK=EC

nên BK=BC

=>B nằm trên đường trung trực của KC(3)

Từ (1),(2),(3) suy ra B,D,I thẳng hàng

A) Chứng minh Tam giác BAD = Tam giác BED

Xét hai tam giác BAD và BED, ta có:

BA = BE (theo giả thiết)
∠BAD = ∠BED (do DE là tia phân giác của ∠B)
Do đó, tam giác BAD = tam giác BED (theo trường hợp cạnh - góc - cạnh).

B) Chứng minh AK = EC

Do tam giác BAD = tam giác BED, ta có AD = ED.

Gọi K là giao điểm của BA và DE, ta có:

AK + KD = AD
EK + KD = ED
Do AD = ED, suy ra AK + KD = EK + KD. Do đó, AK = EK.

C) Chứng minh ba điểm B, D, I thẳng hàng

Gọi I là trung điểm của CK. Do AK = EK và AI = IC (do I là trung điểm), ta có tam giác AKE = tam giác ICE (theo trường hợp cạnh - cạnh - cạnh).

Do đó, ∠AKE = ∠ICE. Khi đó, ta có ∠BKI = ∠BID. Do đó, B, D, I thẳng hàng.

Ta có: AK+KB=AB

AH+HC=AC

mà AK=AH và AB=AC

nên KB=HC

Xét ΔKBC và ΔHCB có

KB=HC

\(\widehat{KBC}=\widehat{HCB}\)

CB chung

Do đó: ΔKBC=ΔHCB

=>\(\widehat{KCB}=\widehat{HBC}\)

=>\(\widehat{OBC}=\widehat{OCB}\)

=>ΔOBC cân tại O

=>OB=OC

=>O nằm trên đường trung trực của BC

Bạn nên ghi hẳn đề bài ra để mọi người hỗ trợ tốt hơn nhé.

Lời giải:

a.

$A(x)=14x^4+(-x^3+x^3)+(3x-5x+x-6x+5x)-1$

$=14x^4-2x-1$
$B(x)=-4x^4-3x^2+(3x+2x+3x)+(-5-5)$
$=-4x^4-3x^2+8x-10$

b,c.

$C(x)=A(x)+B(x)=14x^4-2x-1+(-4x^4-3x^2+8x-10)$

$=14x^4-2x-1-4x^4-3x^2+8x-10$

$=(14x^4-4x^4)-3x^2+(-2x+8x)-(1+10)$

$=10x^4-3x^2+6x-11$

Hệ số cao nhất của $C(x)$ là hệ số gắn liền với đơn thức bậc cao nhất trong cấu tạo của $C(x)$, là $10$
Hệ số tự do của $C(x)$ là hệ số không gắn liền với biến, là $-11$

D(x)=A(x)-B(x)=14x^4-2x-1-(-4x^4-3x^2+8x-10)$

$=14x^4-2x-1+4x^4+3x^2-8x+10$

$=(14x^4+4x^4)+3x^2+(-2x-8x)+(-1+10)$

$=18x^4+3x^2-10x+9$
Hệ số cao nhất của $D(x)$ là $18$

Hệ số tự do của $D(x)$ là $9$

d.

$C(-1)=10(-1)^4-3(-1)^2+6(-1)-11=-10$
$C(1)=10.1^4-3.1^2+6.1-11=2$

$D(1)=18.1^4+3.1^2-10.1+9=20$

$D(0)=18.0^4+3.0^2-10.0+9=9$

4 năm nữa em trả lời nghen

giúp ik :(((

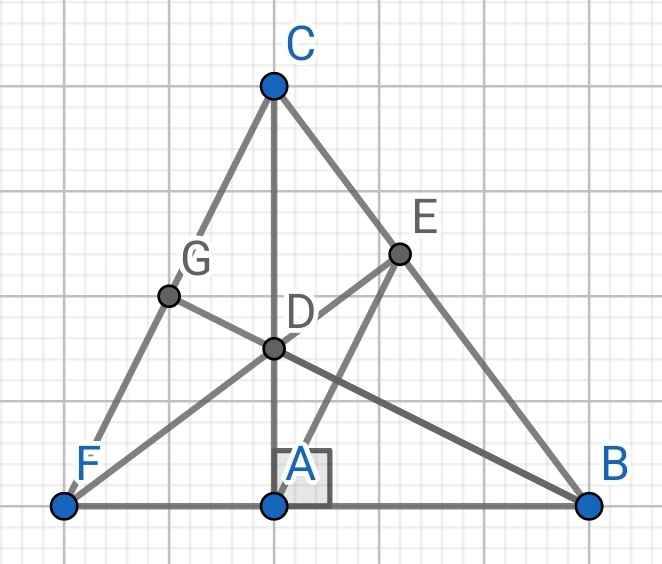
a) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét ∆BDA và ∆BDE có:

BD là cạnh chung

∠ABD = ∠EBD (cmt)

AB = BE (gt)

⇒ ∆BDA = ∆BDE (c-g-c)

b) Do ∆BDA = ∆BDE (cmt)

⇒ AD = DE (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AE (1)

Do BA = BE (gt)

⇒ B nằm trên đường trung trực của AE (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE

⇒ BD ⊥ AE

c) Do ∆BAD = ∆BAE (cmt)

⇒ ∠BAD = ∠BED (hai góc tương ứng)

⇒ ∠BED = 90⁰

⇒ DE ⊥ BE

⇒ DE ⊥ BC

⇒ FE ⊥ BC

⇒ FE là đường cao của ∆BCF

Do CA AB (∆ABC vuông tại A)

⇒ CA ⊥ BF

⇒ CA là đường cao thứ hai của ∆BCF

Mà D là giao điểm của CA và FE

⇒ BD là đường cao thứ ba của ∆BCF

⇒ BD ⊥ CF

Mà BD ⊥ AE (cmt)

⇒ AE // CF

d) Do BD là tia phân giác của ∠ABC (gt)

⇒ BD là tia phân giác của ∠FBC

⇒ BD là đường phân giác của ∆BCF

∆BCF có:

BD là đường cao (cmt)

BD là đường phân giác (cmt)

⇒ ∆BCF cân tại B

⇒ BD là đường trung trực của ∆BCF

Mà M là trung điểm của CF (gt)

⇒ B, D, M thẳng hàng

           Giải:

a; Xét tam giác BDA và tam giác BDE có:

BA = BE (gt)

\(\widehat{ABD}\) = \(\widehat{DBE}\) (gt)

Cạnh BD (chung)

Vậy \(\Delta\) BDA = \(\Delta\) BDE (C-g-c)

b; Xét tam giác ABE có

   BA = BE (gt)

  ⇒ tam giác ABE cân tại B

 BD là phân giác của góc ABE (gt)

 ⇒ BD \(\perp\) AE (vì trong tam giác cân đường phân giác cũng là đường cao)

c; \(\Delta\) BDA = \(\Delta\) BDE (cmt)

⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 90⁰

Xét tam giác vuông EBF và tam giác vuông ABC có:

      BE = AB

      \(\widehat{FBE}\) = \(\widehat{CBA}\)

⇒ \(\Delta\) EBF  =  \(\Delta\) ABC (góc nhọn, cạnh góc vuông)

⇒ BF = BC 

⇒ \(\Delta\) BFC  cân tại B

⇒ BD \(\perp\) FC (trong tam giác cân đường cao cũng là đường phân giác)

Mặt khác BD \(\perp\) AE (cmt)

⇒ AE // FC (vì hai đường thẳng cùng vuông góc đường thẳng thứ ba thì song song với nhau)

d; BD là phân giác của tam giác cân BFC nên BD là đường trung tuyến của FC, mà M là trung điểm CF vậy B, D, M thẳng hàng vì qua một đỉnh của tam giác chỉ kẻ được một trung tuyến ứng với cạnh đối diện của đỉnh đó. 

Đề bài cụ thể là gì vậy bạn?