cho ∆ abc có hai đường cao bd và ce cắt nhau tại h . gọi M là trung điểm của ED và N là trung điểm của BC chứng minh rằng a, ∆HEB~∆HBC. b, AB.AE=AC AD từ đó suy ra góc AED = góc ACB. c, MN vuông góc với ED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Tích hai số sau lớn hơn tích hai số đầu là 192 nên ta có:
\(\left(a+2\right)\left(a+1\right)-a\left(a+1\right)=192\)
=>\(a^2+3a+2-a^2-a=192\)
=>2a+2=192
=>a+1=96
=>a=95
=>a+1=96; a+2=97
vậy: ba số cần tìm là 95;96;97
Gọi 3 STN liên tiếp lần lượt là: \(x;x+1;x+2\left(ĐK:x\inℕ\right)\)
Tích hai số sau: \(\left(x+1\right)\left(x+2\right)\) và tích hai số đầu: \(x\left(x+1\right)\)
Theo bài ra, ta có:
\(\left(x+1\right)\left(x+2\right)-x\left(x+1\right)=192\\ \Rightarrow x^2+x+2x+2-x^2-x=192\\ \Rightarrow2x=190\\ \Rightarrow x=95\left(TM\right)\)
Vậy 3 STN phải tìm: 95;96;97

Gọi hai số cần tìm là a,b
Tổng của chúng gấp 5 lần hiệu của chúng nên ta có:
\(a+b=5\left(a-b\right)\)
=>\(5a-5b=a+b\)
=>4a=6b
=>2a=3b
=>\(\dfrac{a}{3}=\dfrac{b}{2}=k\)
=>a=3k; b=2k
Tích của chúng bằng 24 lần hiệu của chúng nên ta có:
\(a\cdot b=24\left(a-b\right)\)
=>\(2k\cdot3k=24\left(3k-2k\right)\)
=>\(6k^2=24k\)
=>\(k^2=4k\)
=>k(k-4)=0
=>\(\left[{}\begin{matrix}k=0\\k=4\end{matrix}\right.\)
TH1: k=0
=>\(a=3\cdot0=0;b=2\cdot0=0\)
TH2: k=4
=>\(a=3\cdot4=12;b=2\cdot4=8\)

\(3\cdot\left(-35\right)\cdot\left(-37\right)-\left(-15\right)\cdot37\)
\(=105\cdot37+15\cdot37\)
\(=37\left(105+15\right)=37\cdot120=4440\)
4,(-35).15 -(-15)-37 5,(-154).(-235)+154.(-35) 6,(-25).(-17).4+(-20)

\(1.237.\left(-28\right)+28.137\)
\(=237.\left(-28\right)+28.137\)
\(=\left(-237\right).28+28.137\)
\(=28.\left[\left(-237\right)+137\right]\)
\(=28.\left(-100\right)\)
\(=-2800\)
1237 x (-28) + 28 x 137
= 1237 x (-28) - (-28) x 137
= (-28) x (1237 - 137)
= (-28) x 1100
= (-28) x (1000 + 100)
= (-28) x 1000 + (-28) x 100
= (-28000) + (-2800)
= (-30800)


A = a(b² + c²) + b(a² + c²) + c(a² + b²) + 3abc
= ab² + ac² + a²b + bc² + a²c + b²c + 3abc
= (ab² + a²b + abc) + (a²c + ac² + abc) + (b²c + bc² + abc)
= ab(a + b + c) + ac(a + c + b) + bc(b + c + a)
= (a + b + c)(ab + ac + bc)
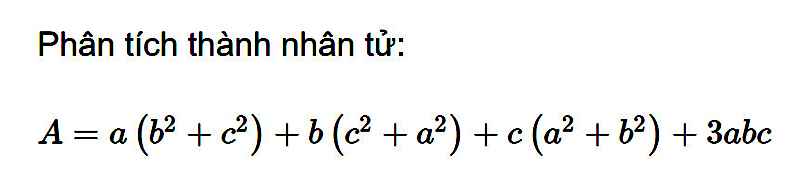
a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB~ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE~ΔABC
=>\(\widehat{AED}=\widehat{ACB}\)
c: Ta có: ΔEBC vuông tại E
mà EN là đường trung tuyến
nên \(NE=\dfrac{BC}{2}\left(1\right)\)
ΔDBC vuông tại D
mà DN là đường trung tuyến
nên \(DN=\dfrac{BC}{2}\left(2\right)\)
Từ (1),(2) suy ra ND=NE
=>ΔNDE cân tại N
ΔNDE cân tại N
mà NM là đường trung tuyến
nên NM\(\perp\)DE