Hãy kể tên các vị vua trong lịch sử việt nam
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{3}{x+1}-\dfrac{3x+2}{x^3+1}\)(ĐKXĐ: x<>-1)
\(=\dfrac{3}{x+1}-\dfrac{3x+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3\left(x^2-x+1\right)-3x-2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3x^2-3x+3-3x-2}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{3x^2-6x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(m^2(x-1)=2(2x-3)+m\\\Leftrightarrow m^2x-m^2=4x-6+m\\\Leftrightarrow m^2x-4x=m^2+m-6\\\Leftrightarrow (m^2-4)x=(m-2)(m+3)\text{ (1) }\)
+, Xét \(m^2-4=0\Leftrightarrow m=\pm2\)
*) Với \(m=2\) thì pt (1) trở thành:
\(\left(2^2-4\right)x=\left(2-2\right)\left(2+3\right)\)
\(\Leftrightarrow0x=0\) (luôn đúng)
\(\Rightarrow m=2\) thì pt (1) có vô số nghiệm
*) Với \(m=-2\) thì pt (1) trở thành:
\(\left[\left(-2\right)^2-4\right]x=\left(-2-2\right)\left(-2+3\right)\)
\(\Leftrightarrow0x=-4\) (vô lí)
\(\Rightarrow m=-2\) thì pt vô nghiệm
+, Xét \(m^2-4\ne0\Leftrightarrow m\ne\pm2\)
Khi đó, pt (1) tương đương:
\(\left(m-2\right)\left(m+2\right)x=\left(m-2\right)\left(m+3\right)\)
\(\Leftrightarrow x=\dfrac{m+3}{m+2}\) (do \(m\ne\pm2\)) \(\Rightarrow m\ne\pm2\) thì pt có nghiệm \(x=\dfrac{m+3}{m+2}\).
Vậy: ...

Đây là dạng toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp bezout như sau.
\(x^2\) + \(x\) - \(xy\) = 3y + 5
\(x^2\) + \(x\) - 5 = 3y + \(xy\)
\(x^2\) + \(x\) - 5 = y.(3 + \(x\))
y = \(\dfrac{x^2+x-5}{3+x}\) (1); (đk \(x\) ≠ -3)
y \(\in\) Z ⇔ \(x^2\) + \(x\) - 5 ⋮ 3 + \(x\)
Theo bezout ta có:
\(x^2\) + \(x\) - 5 ⋮ 3 + \(x\)
⇔ (-3)2 + (-3) - 5 ⋮ 3 + \(x\)
⇔ 1 ⋮ 3 + \(x\)
3 + \(x\) \(\in\) Ư(1) = {-1; 1}
\(x\) \(\in\) {-4; -2}
Lập bảng ta có:
| \(x\) | - 4 | -2 |
| y = \(\dfrac{x^2+x-5}{3+x}\) | -7 | -3 |
Theo bảng trên ta có: (\(x;y\)) = (-4; -7); (-2; -3)
Vậy (\(x;y\)) = (-4; -7); (-2; -3)

Bạn thử code này nhé
program RENUM;
var
S: string;
frequency: array[0..9] of integer; // Mảng đếm số lần xuất hiện của các số từ 0 đến 9
maxFreq, maxNum, i, num: integer;
begin
// Khởi tạo tất cả các phần tử trong mảng đếm về 0
for i := 0 to 9 do
frequency[i] := 0;
// Nhập xâu ký tự S từ bàn phím
writeln('Nhap vao xau ky tu S: ');
readln(S);
// Đếm số lần xuất hiện của các số từ 0 đến 9 trong xâu S
for i := 1 to length(S) do
begin
if (S[i] >= '0') and (S[i] <= '9') then
begin
num := ord(S[i]) - ord('0');
frequency[num] := frequency[num] + 1;
end;
end;
// Tìm số có số lần xuất hiện nhiều nhất và nhỏ nhất
maxFreq := 0;
maxNum := 0;
for i := 0 to 9 do
begin
if frequency[i] > maxFreq then
begin
maxFreq := frequency[i];
maxNum := i;
end;
end;
// In ra số xuất hiện nhiều nhất
if maxFreq > 0 then
writeln('So xuat hien nhieu nhat la: ', maxNum)
else
writeln('Trong xau khong co so nao.');
readln;
end.

Giải
Số hình lập phương được sơn đúng một mặt là:
(4 - 2) x (4 - 2) x 6 = 24 (hình)
Số hình lập phương có đúng hai mặt được sơn là:
(4 - 2) x 12 = 24 (hình)
Kết luận: a, có 24 hình lập phương nhỏ được sơn đúng một mặt
có 24 hình lập phương nhỏ được sơn đúng hai mặt
a) Ở mỗi mặt, có hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).
Ở sáu mặt có: (hình).
b) Ở mỗi cạnh, có hình lập phương được sơn hai mặt (các hình ghi dấu "").
Ở cạnh có : (hình).

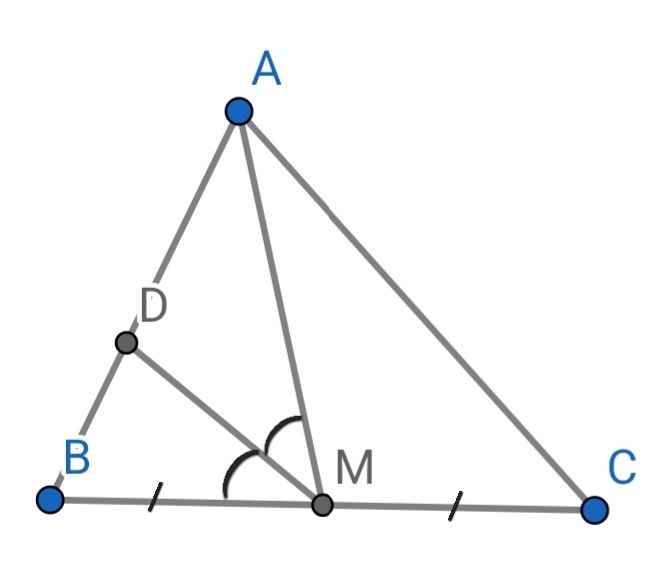
Do M là trung điểm của BC (gt)
⇒ BM = BC : 2 = 30 : 2 = 15 (cm)
BD = AB - AD = 10 - 6 = 4 (cm)
Do MD là đường phân giác của ∆AMB (gt)
⇒ AD/BD = AM/BM
⇒ AM = AD . BM : BD
= 6 . 15 : 4
= 22,5 (cm)
Ta có:
Suy ra cm
là trung tuyến của suy ra là trung điểm của
Suy ra cm.
Xét có là phân giác của góc nên
Do đó (cm).

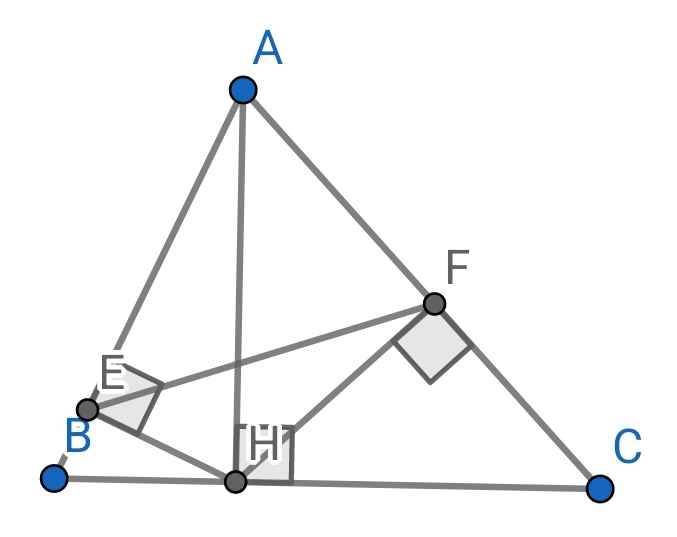
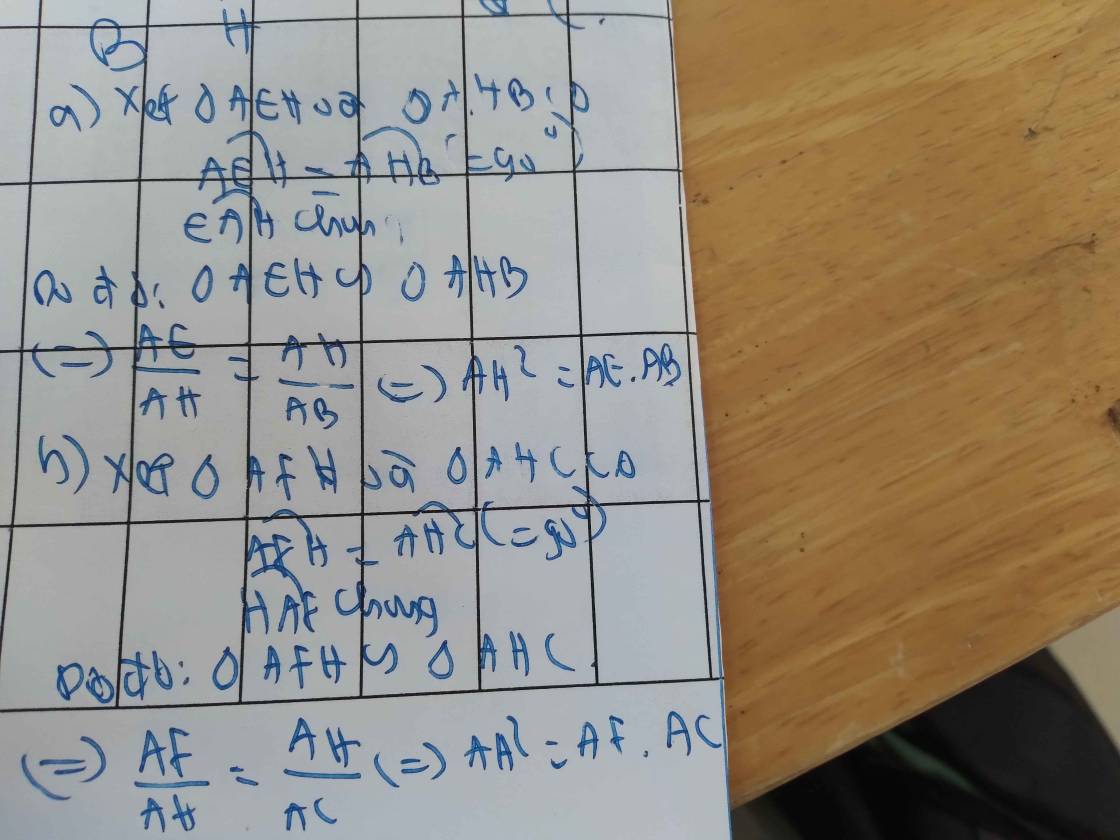
a) Xét hai tam giác vuông: ∆AEH và ∆AHB có:
∠A chung
⇒ ∆AEH ∽ ∆AHB (g-g)
⇒ AH/AB = AE/AH
⇒ AH² = AE.AB
b) Xét hai tam giác vuông: ∆AFH và ∆AHC có:
∠A chung
⇒ ∆AFH ∽ ∆AHC (g-g)
⇒ AH/AC = AF/AH
⇒ AH² = AF.AC
Mà AH² = AE.AB (cmt)
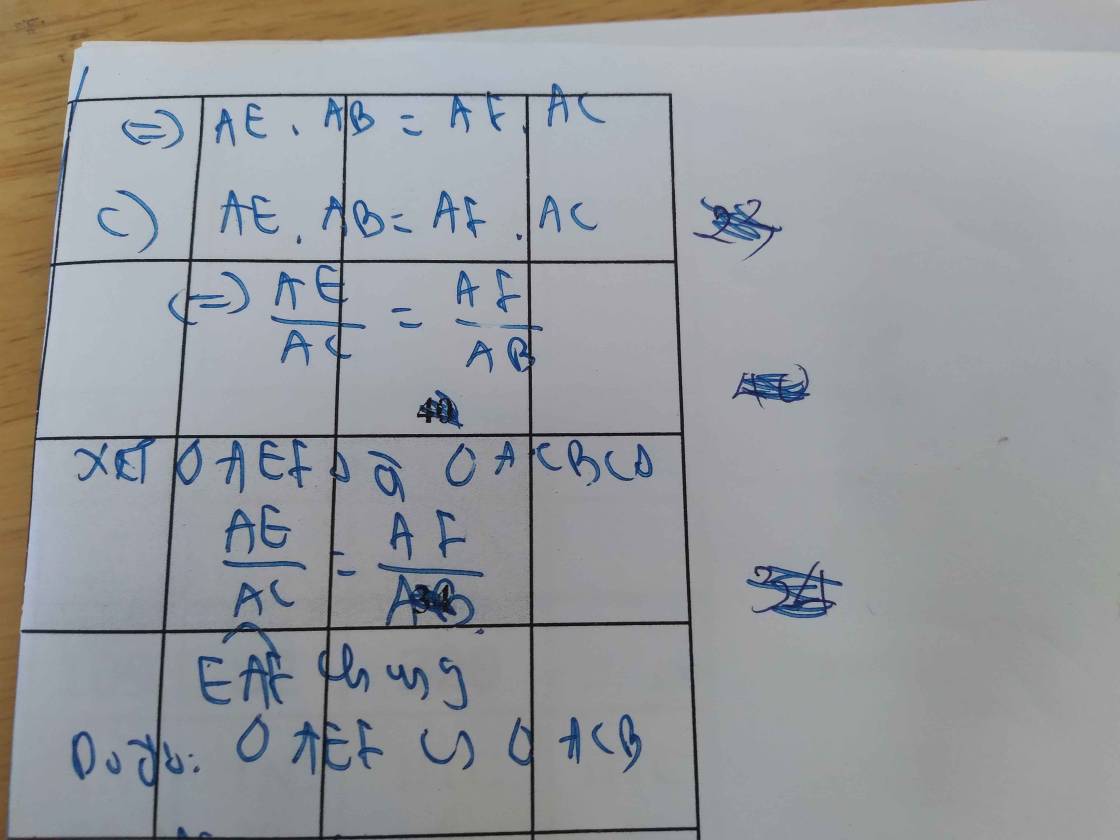
⇒ AE.AB = AF.AC
c) Do AE.AB = AF.AC (cmt)
⇒ AE/AC = AF/AB
Xét ∆AEF và ∆ACB có:
AE/AC = AF/AB (cmt)
∠A chung
⇒ ∆AEF ∽ ∆ACB (c-g-c)
Gọi p và p' lần lượt là chu vi của ∆AEF và ∆ACB
⇒ p/p' = 20/30= 2/3
Do ∆AEF ∽ ∆ACB (cmt)
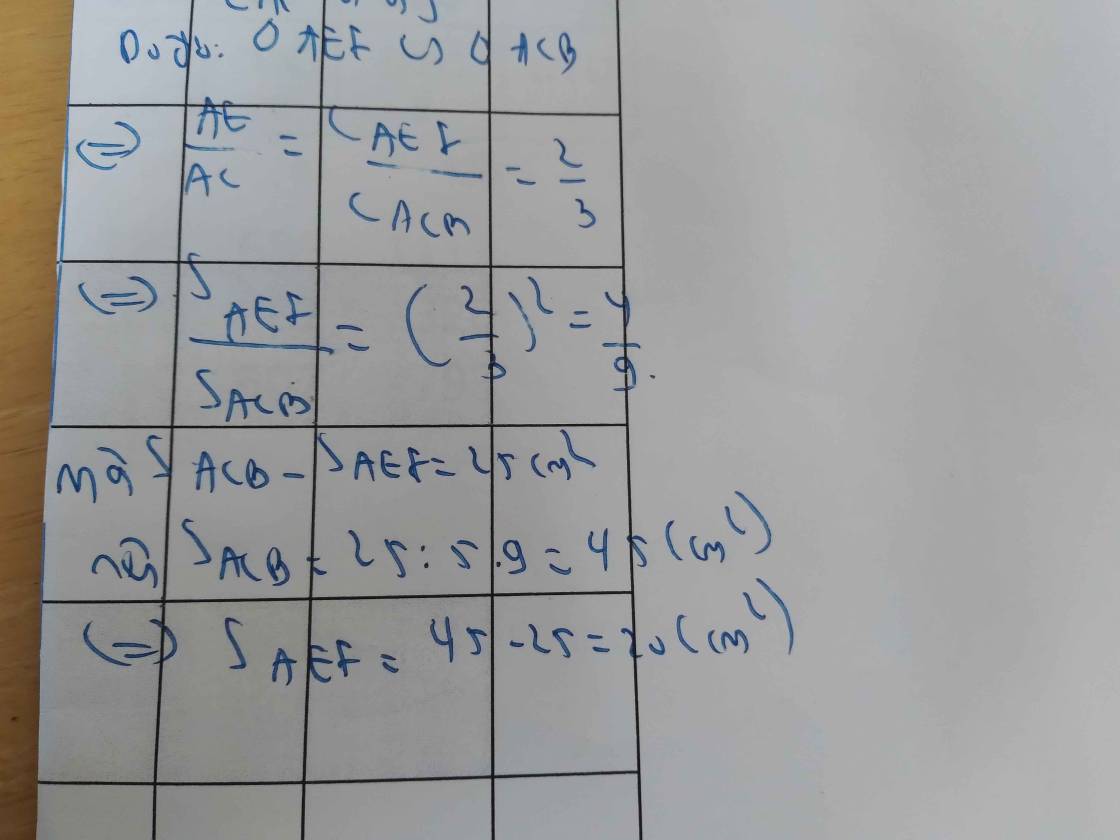
⇒ AE/AC = AF/AB = EF/BC = p/p' = 2/3
Gọi x, y lần lượt là diện tích của ∆AEF và ∆ACB
Do ∆AEF ∽ ∆ACB (cmt)
⇒ x/y = (2/3)² = 4/9
⇒ x/4 = y/9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/4 = y/9 = (y - x)/(9 - 4) = 25/5 = 5
x/4 = 5 ⇒ x = 5.4 = 20 (cm²)
y/9 = 5 ⇒ y = 5.9 = 45 (cm²)
Vậy diện tích ∆AEF là 20 cm², diện tích ∆ACB là 45 cm²

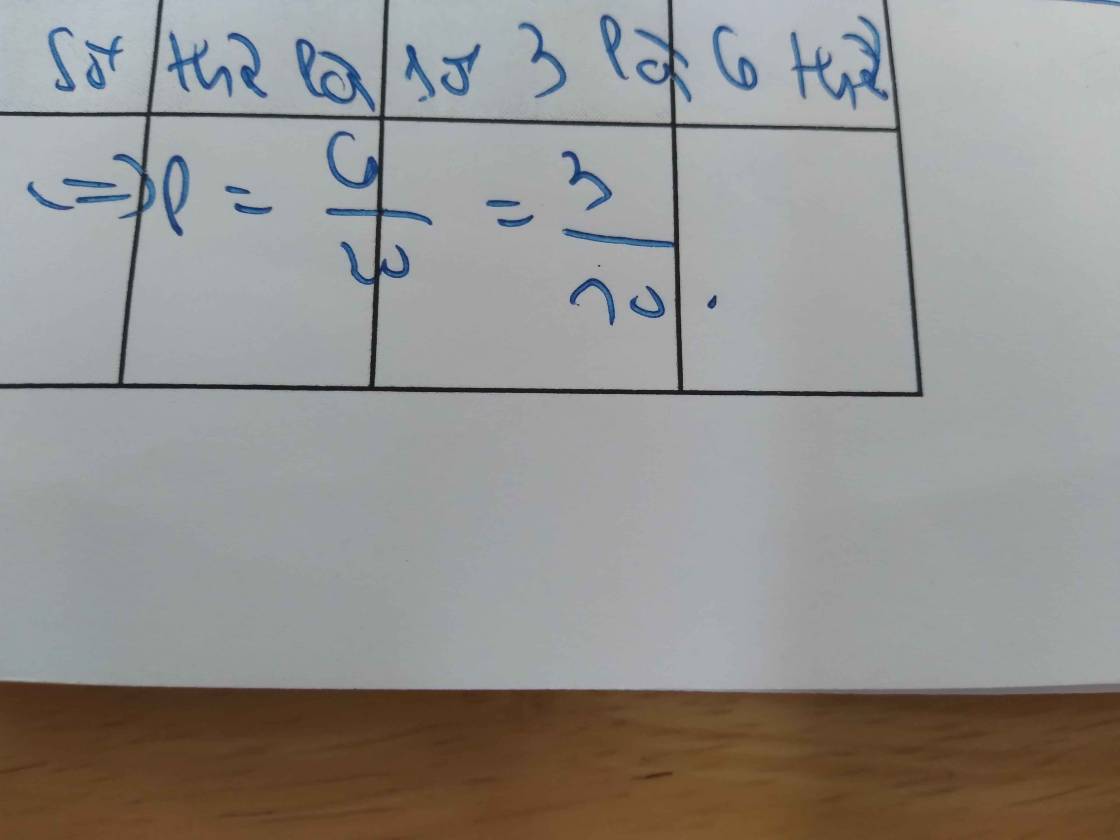
Có 6 khả năng rút được thẻ số 3 nên xác suất của biến cố "Thẻ rút ra là thẻ đánh số 3" là:
P = 6/20 = 3/10

Giải:
Đổi 1 giờ 30 phút = 1,5 giờ
Cứ một giờ ca nô xuôi dòng được: 1 : 1,5 = \(\dfrac{2}{3}\)(quãng sông AB)
Cứ một giờ ca nô ngược dòng được: 1 : 2 = \(\dfrac{1}{2}\) (quãng sông AB)
Cứ một giờ dòng nước chảy được: (\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) : 2 = \(\dfrac{1}{12}\)(quãng sông AB)
Quãng sông AB dài là: 3 : \(\dfrac{1}{12}\) = 36 (km)
Vận tốc ca nô khi ngược dòng là: 36 : 2 = 18 (km/h)
Vận tốc riêng của ca nô là: 18 + 3 = 21 (km/h)
Kết luận: Quãng sông AB dài 36 km
Vận tốc riêng của ca nô là 21 km/h
Gọi x (km/h) là vận tốc riêng của ca nô (x > 3)
Vận tốc đi xuôi dòng từ A đến B: x + 3 (km/h)
1 giờ 30 phút = 1,5 giờ
Quãng đường đi xuôi dòng: (x + 3).1,5 (km)
Vận tốc đi ngược dòng từ B về A: x - 3 (km/h)
Quãng đường đi ngược dòng: (x - 3).2 (km)
Do đi cùng một quãng đường AB nên ta có phương trình:
(x + 3).1,5 = (x - 3).2
1,5x + 4,5 = 2x - 6
2x - 1,5x = 4,5 + 6
0,5x = 10,5
x = 10,5 : 0,5
x = 21 (nhận)
Vậy vận tốc riêng của ca nô là 21 km/h
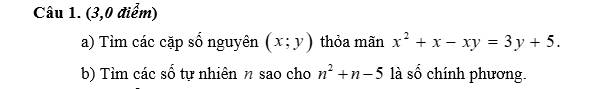
Tham khỏa : mình cop mạng
Nhà Mạc
<p mso-margin-top-alt:auto;text-align:center;margin-bottom:auto"="" style="box-sizing: border-box; margin: 0px 0px 10px;">(1527 - 1592)Mạc Thái Tổ (Đăng Dung)
1527 – 1529
Minh Đức
Mạc Thái Tông (Đăng Doanh)
1530 – 1540
Đại Chính
Mạc Hiến Tông
(Phúc Hải)
1541 – 1546
Quảng Hoà
Mạc Tuyên Tông
(Phúc Nguyên)
1546 -1561
Vĩnh Định (1547), Cảnh Lịch (1548 - 1553), Quang Bảo (1554 - 1561)
Mạc Mậu Hợp
1562 - 1592
Thuần Phúc (1562 - 1565), Sùng Khang (1566 - 1577), Diên Thành (1578 - 1585),Đoan Thái (1586 - 1587), Hưng Trị (1590), Hồng Ninh (1591 - 1592)
Nhà Hậu Lê
(Lê Trung Hưng)
Lê Trang Tông
1533 – 1548
Nguyên Hoà
Lê Trung Tông
1548 – 1556
Thuận Bình
Lê Anh Tông
1556 – 1573
Thiên Hữu (1557), Chính Trị (1588 - 1571), Hồng Phúc (1572 – 1573)
Lê Thế Tông
1573 – 1599
Gia Thái (1573 - 1577), Quang Hưng (1578 – 1599)
Lê Kính Tông
1600 - 1619
Thuận Đức (1600), Hoằng Định (1601 1919)
Lê Thần Tông
1619 - 1643
Vĩnh Tộ (1620 - 1628), Đức Long (1629 - 1634), Dương Hoà (1635 - 1643)
Lê Chân Tông
1643 - 1649
Phúc Thái
Lê Thần Tông
1649 - 1662
Khánh Đức (1649 - 1652), Thịnh Đức (1653 - 1657), Vĩnh Thọ (1658 - 1662), Vạn Khánh (1662). Thần Tông làm vua lần thứ 2 sau khi Chân Tông chết không có con nối dõi
Lê Huyền Tông
1662 - 1671
Cảnh Trị
Lê Gia Tông
1672 – 1675
Dương Đức (1672 - 1673), Đức Nguyên (1674 - 1675)
Lê Hy Tông
1676 – 1705
Vĩnh Trị (1676 – 1680), Chính Hoà (1681 - 1705)
Lê Dụ Tông
1705 – 1728
Vĩnh Thịnh (1705 - 1720), Bảo Thái (1720 - 1729)
Lê Đế Duy Phường (Hôn Đức Công)
1729 – 1732
Vĩnh Khánh
Lê Thuần Tông
1732 – 1735
Long Đức
Lê Ý Tông
1735 – 1740
Vĩnh Hựu
Lê Hiển Tông
1740 – 1786
Cảnh Hưng
Lê Mẫn Đế
1787 - 1789
Chiêu Thống
Triều Tây Sơn
Thái Đức Hoàng Đế (Nguyễn Nhạc)
1778 – 1793
Thái Đức
(1778 - 1802)
Quang Trung Hoàng Đế (Nguyễn Huệ)
1789 – 1792
Quang Trung
Cảnh Thịnh Hoàng Đế (Nguyễn Quang Toản)
1792 - 1802
Cảnh Thịnh (1792 - 1801), Bảo Hưng (1801 – 1802)
Chúa Trịnh
Trịnh Kiểm
1545 – 1569
Trịnh Cối
1569 – 1570
Trịnh Tùng
1570 – 1623
Thành Tổ Triết Vương
Trịnh Tráng
1623 – 1652
Văn Tổ Nghị Vương
Trịnh Tạc
1653 – 1682
Hoằng Tổ Dương Vương
Trịnh Căn
1682 – 1709
Chiêu Tổ Khang Vương
Trịnh Bách
1684
Trịnh Bính
1688
Trịnh Cương
1709 – 1729
Hy Tổ Nhân Vương
Trịnh Giang
1729 – 1740
Dụ Tổ Thuận Vương
Trịnh Doanh
1740 – 1767
Nghị Tổ Ân Vương
Trịnh Sâm
1767 – 1782
Thái Tổ Thịnh Vương
Trịnh Cán
1782
Trịnh Tông (Tr.Khải)
1782 – 1786
Đoan Nam Vương
Trịnh Bồng
1786 - 1787
Án Đô Vương
Chúa Nguyễn
1600 - 1802
Nguyễn Hoàng
1600 – 1613
Nguyễn Phúc Nguyên
1613 – 1635
Nguyễn Phúc Lan
1635 – 1648
Nguyễn Phúc Tần
1648 – 1687
Nguyễn Phúc Trăn
1687 – 1691
Nguyễn Phúc Chu
1691 – 1725
Nguyễn Phúc Chú
1725 – 1738
Nguyễn Phúc Khoát
1738 – 1765
Nguyễn Phúc Thuần
1765 – 1777
Nguyễn Phúc Ánh
1780 - 1802
Nhà Nguyễn
1802 - 1945
Nguyễn Thế Tổ
1802 – 1819
Gia Long
Nguyễn Thánh Tổ
1820 – 1840
Minh Mạng
Nguyễn Hiến Tổ
1841 – 1847
Thiệu Trị
Nguyễn Dực Tông
1848 – 1883
Tự Đức
Nguyễn Dục Đức
1883
Làm vua được 3 ngày
Nguyễn Hiệp Hoà
6 - 11/1883
Hiệp Hoà
Nguyễn Giản Tông
12 – 8/1884
Kiến Phúc
Nguyễn Hàm Nghi
1884 – 1885
Hàm Nghi
Nguyễn Cảnh Tông
1885 – 1888
Đồng Khánh
Nguyễn Thành Thái
1889 – 1907
Thành Thái
Nguyễn Duy Tân
1907 – 1916
Duy Tân
Nguyễn Hoằng Tông
1916 – 1925
Khải Định
Nguyễn Bảo Đại
1925 - 1945
Bảo Đại