Lời giải:
$A=a^2+ab+b^2-3b-3a+3$

$4A=4a^2+4ab+4b^2-12a-12b+12$

$=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+9+(3b^2-6b+3)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $A_{\min}=0$. Giá trị này đạt tại $2a+b-3=b-1=0$

$\Leftrightarrow b=1; a=1$

Câu B tương tự câu A nhé. Chỉ khác mỗi đặt tên biến.

---------------

$C=x^2+5y^2-4xy+2y-3$

$=(x^2-4xy+4y^2)+(y^2+2y)-3$

$=(x-2y)^2+(y^2+2y+1)-4$

$=(x-2y)^2+(y+1)^2-4\geq 0+0-4=-4$

Vậy $C_{\min}=-4$. Giá trị này đạt tại $x-2y=y+1=0$

$\Leftrightarrow y=-1; x=-2$

Lời giải:

$x^3+y^3=(x+y)^3-3xy(x+y)=2^3-3xy.2=8-6xy$

$=8-3.2xy=8-3[(x+y)^2-(x^2+y^2)]=8-3(2^2-34)=98$

----------------

$x^4+y^4=(x^2+y^2)^2-2x^2y^2=34^2-\frac{1}{2}(2xy)^2$

$=34^2-\frac{1}{2}[(x+y)^2-(x^2+y^2)]^2=34^2-\frac{1}{2}(2^2-34)^2=706$

Đề sai, em xem lại đề nhé

Lời giải:

a. Áp dụng định lý Pitago: 

$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) 

Dễ thấy $DM$ là đường trung bình của tam giác ABC ứng với cạnh $AC$

$\Rightarrow DM\parallel AC$

$\Rightarrow DM\perp AB$

Tam giác $MBD$ và $MAD$ có:

$BD=DA$

$\widehat{MDB}=\widehat{MDA}=90^0$

$DM$ chung

$\Rightarrow \triangle MBD=\triangle MAD$ (c.g.c)

$\Rightarrow MA=MB=\frac{BC}{2}=10:2=5$ (cm)

c.

Tứ giác $AEBM$ có 2 đường chéo $AB, EM$ cắt nhau tại trung điểm $D$ của mỗi đường nên $AEBM$ là hình bình hành.

Mà $AB\perp EM$ ở $D$ (suy ra từ việc cm $MD\perp AB$)

$\Rightarrow AEBM$ là hình thoi.

c.

Để $AEBM$ là hình vuông thì $\widehat{AMB}=90^0$

$\Leftrightarrow AM\perp BC$

$\Leftrightarrow$ trung tuyến $AM$ đồng thời là đường cao 

$\Leftrightarrow \triangle ABC$ cân tại $A$

Hình vẽ:

\(3x^2+2y^2=5xy\)

\(\Leftrightarrow3x^2+2y^2-5xy=0\)

\(\Leftrightarrow2\left(x^2-2xy+y^2\right)+x^2-xy=0\)

\(\Leftrightarrow2\left(x-y\right)^2+x\left(x-y\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left[2\left(x-y\right)+x\right]=0\)

\(\Leftrightarrow\left(x-y\right)\left(3x-2y\right)=0\)

\(\Leftrightarrow3x-2y=0\Leftrightarrow x=\dfrac{2y}{3}\) Thay vào S

\(\Rightarrow S=\dfrac{y+\dfrac{4y}{3}}{y-\dfrac{4y}{3}}=-7\)

P = \(\dfrac{2x+3}{x+3}\) (đk \(x\ne\) - 3; \(x\in\) Z^-

P \(\in\) Z ⇔ 2\(x\) + 3 ⋮ \(x\) + 3

              2\(x\) + 6  -3 ⋮ \(x\) + 3

          2.(\(x\) + 3) - 3 ⋮ \(x\) + 3

                          3  \(⋮\)  \(x\) + 3

\(x\) + 3 \(\in\) Ư(3) = {-3;  -1; 1; 3}

Lập bảng ta có: 

Vì  \(x\) \(\in\) Z^- nên theo bảng trên ta có:

\(x\) \(\in\) {- 6; - 4; -2}

Ta có

\(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\Rightarrow\dfrac{BM}{AM}=\dfrac{CN}{AN}\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\) => MN//BC (Talet)

\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\)  (1)

Ta có

\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\Rightarrow\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{a+b}\)

\(\Rightarrow AM=\dfrac{b^2}{a+b}\) Thay vào (1)

\(\Rightarrow\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{a+b}=\dfrac{MN}{a}\Rightarrow MN=\dfrac{ab}{a+b}\)

Ta có

����=����=��AMBM​=ACBC​=ba​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

����=����=��ANCN​=ABBC​=ba​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

⇒����=����⇒����=����⇒AMBM​=ANCN​⇒CNBM​=ANAM​ => MN//BC (Talet)

⇒����=����⇒���=���⇒ABAM​=BCMN​⇒bAM​=aMN​  (1)

Ta có

����=����=��BMAM​=BCAC​=ab​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

⇒���=���=��+���+�=���+�=��+�⇒bAM​=aBM​=a+bAM+BM​=a+bAB​=a+bb​

⇒��=�2�+�⇒AM=a+bb2​ Thay vào (1)

⇒�2�+��=���⇒��+�=���⇒��=���+�⇒ba+bb2​​=aMN​⇒a+bb​=aMN​⇒MN=a+bab​
 

\(\left(-\dfrac{3x}{5y^2}\right).\left(-\dfrac{5y^2}{6x^3}\right)\)

\(=\dfrac{-3x.\left(-5y^2\right)}{5y^2.6x^3}\)

\(=\dfrac{1}{2x^2}\)

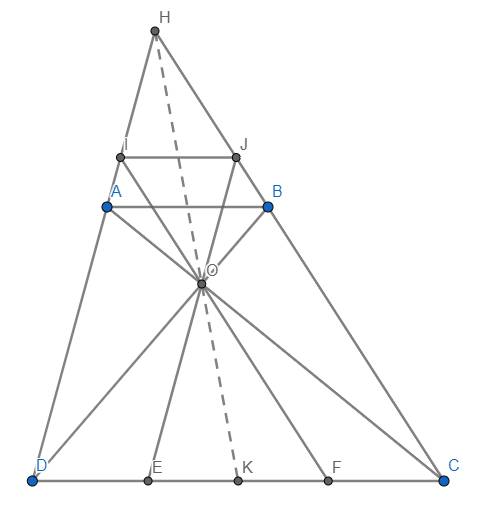
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)

Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)

c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)

Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\) 

Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB

d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)