Gọi hai góc so le trong là \(\widehat{AEF};\widehat{EFD}\); Ey;Fx lần lượt là phân giác của góc AEF;góc EFD

Vì AB//CD nên \(\widehat{AEF}=\widehat{EFD}\)(hai góc so le trong)

mà \(\widehat{yEF}=\dfrac{\widehat{AEF}}{2};\widehat{xFE}=\dfrac{\widehat{EFD}}{2}\)

nên \(\widehat{yEF}=\widehat{xFE}\)

mà hai góc này là hai góc ở vị trí so le trong

nên Ey//Fx

a) TH1: x = 1 

=> Giá tiền phải trả là: 11000 (đồng) 

TH2: x > 1 

=> Giá tiền phải trả là:

11000 + 10000(x - 1) 

= 11000 + 10000x - 10000 

= 10000x + 1000 (đồng) (1) 

b) Người đó đi 50km ta thay x = 50 vào (1) ta có:

10000*50 + 1000 

= 500000 + 1000 

= 501000 (đồng) 

Bài 4: \(8^{10}\cdot125^{10}< =2^n\cdot5^n< =20^{16}\cdot5^{16}\)

=>\(1000^{10}< =10^n< =100^{16}\)

=>\(10^{30}< =10^n< =10^{32}\)

=>30<=n<=32

mà n là số tự nhiên

nên \(n\in\left\{30;31;32\right\}\)

Bài 1:

1: \(3^{-2}\cdot3^4\cdot3^n=3^7\)

=>\(3^n\cdot3^2=3^7\)

=>n+2=7

=>n=7-2=5

2: \(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)

=>\(2^n\left(\dfrac{1}{2}+4\right)=2^5\cdot9\)

=>\(2^n=9\cdot2^5:\dfrac{9}{2}=2^6\)

=>n=6

Bài 2:

1: \(243>=3^n>=9\)

=>\(3^2< =3^n< =3^5\)

=>2<=n<=5

mà n là số tự nhiên

nên \(n\in\left\{2;3;4;5\right\}\)

2: \(2^{n+3}\cdot2^n=144\)

=>\(2^{2n+3}=144\)

=>\(2n+3=log_2144\)

=>\(2n=log_2144-3\)

=>\(n=\dfrac{log_2144-3}{2}\left(loại\right)\)

Bài 3:

\(10^x:5^y=20^y\)

=>\(10^x=20^y\cdot5^y=100^y=10^{2y}\)

=>x=2y

vậy: \(\left(x;y\right)\in\){(2k;k)|\(k\in N\)}

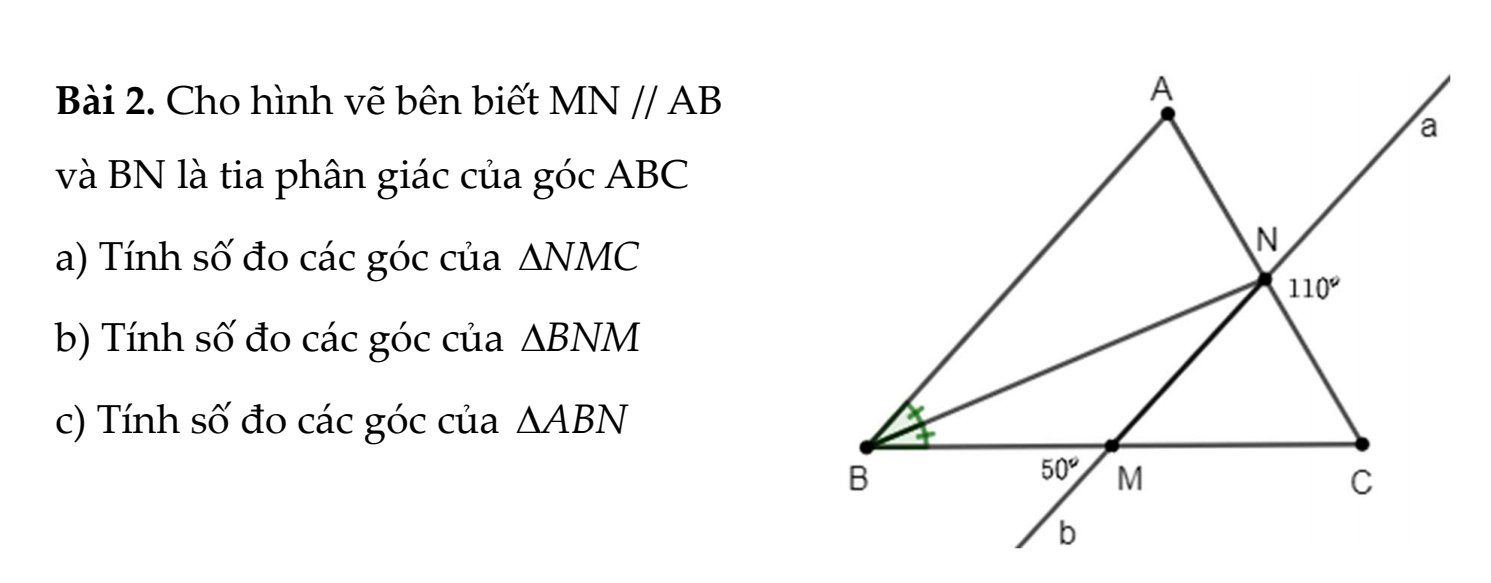
a: Ta có: \(\widehat{bMB}=\widehat{NMC}\)(hai góc đối đỉnh)

mà \(\widehat{bMB}=50^0\)

nên \(\widehat{NMC}=50^0\)

Ta có: \(\widehat{MNC}+\widehat{aNC}=180^0\)(hai góc kề bù)

=>\(\widehat{MNC}+110^0=180^0\)

=>\(\widehat{MNC}=70^0\)

Xét ΔMNC có \(\widehat{NMC}+\widehat{MNC}+\widehat{C}=180^0\)

=>\(\widehat{C}+50^0+70^0=180^0\)

=>\(\widehat{C}=60^0\)

b: Ta có: \(\widehat{NMB}+\widehat{NMC}=180^0\)(hai góc kề bù)

=>\(\widehat{NMB}+50^0=180^0\)

=>\(\widehat{NMB}=130^0\)

Ta có: MN//AB

=>\(\widehat{CMN}=\widehat{CBA}\)(hai góc đồng vị)

=>\(\widehat{CBA}=50^0\)

BN là phân giác của góc CBA

=>\(\widehat{NBM}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔNMB có \(\widehat{NMB}+\widehat{BNM}+\widehat{NBM}=180^0\)

=>\(\widehat{MNB}=180^0-130^0-25^0=25^0\)

c: BN là phân giác của góc CBA

=>\(\widehat{ABN}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

=>\(\widehat{BAN}+60^0+50^0=180^0\)

=>\(\widehat{BAN}=70^0\)

Xét ΔBAN có \(\widehat{BAN}+\widehat{ABN}+\widehat{ANB}=180^0\)

=>\(\widehat{ANB}=180^0-75^0-25^0=85^0\)

\(\dfrac{15}{34}+\dfrac{15}{17}+\dfrac{19}{34}-1\dfrac{15}{17}+\dfrac{2}{3}\)

\(=\dfrac{15}{34}+\dfrac{19}{34}+\dfrac{15}{17}-1-\dfrac{15}{17}+\dfrac{2}{3}\)

\(=1-1+\dfrac{2}{3}=\dfrac{2}{3}\)

\(\dfrac{11}{5}-\left(0,35+x\right)=1\dfrac{1}{2}\\ \dfrac{11}{5}-\left(\dfrac{7}{20}+x\right)=\dfrac{3}{2}\\ \dfrac{11}{5}-\dfrac{7}{20}-x=\dfrac{3}{2}\\ \dfrac{44}{20}-\dfrac{7}{20}-x=\dfrac{3}{2}\\ \dfrac{37}{20}-x=\dfrac{3}{2}\\ x=\dfrac{37}{20}-\dfrac{3}{2}\\ x=\dfrac{7}{20}\)

`4^3<=2^x<=2^10`

`=>(2^2)^3<=2^x<=2^10`

`=>2^(2*3)<=2^x<=2^10`

`=>2^6<=2^x<=2^10`

`=>6<=x<=10` 

giúp mình với ạ

\(\left(9-\dfrac{1}{2}-\dfrac{3}{4}\right):\left(7-\dfrac{1}{4}-\dfrac{5}{8}\right)\)

\(=\left(\dfrac{36}{4}-\dfrac{2}{4}-\dfrac{3}{4}\right):\left(\dfrac{56}{8}-\dfrac{2}{8}-\dfrac{5}{8}\right)\)

\(=\dfrac{31}{4}:\dfrac{49}{8}=\dfrac{31}{4}\cdot\dfrac{8}{49}=\dfrac{62}{49}\)