Để giải dạng bài này ta phải quy các góc về 1 duy nhất ví dụ quy tất cả ra góc A

có: 2A = 3B => B=2A/3

2A = 4C => C= 2A/4= A/2

2A=6D => D=2A/6 = A/3

A+B+C+D = A + 2A/3 + A/2 + A/3

=A(1+2/3 + 1/2 + 1/3)

=5A/2 = 360 độ

=> A = 360x2/5 = 144 độ

B =2A/3 = 2x144/3= 96 độ

C = A/2 = 144/2 = 72 độ

D=  A/3 = 144/3 = 48 độ

Mọi thắc mắc tới toán có thể liên hệ để được giải đáp thêm

Nửa chu vi hcn là: `78:2=39(m)`

Gọi chiều dài hcn ban đầu là: `x (m)`       `ĐK: 3 < x < 39`

`=>` Chiều rộng hcn ban đầu là: `39-x(m)`

Vì nếu giảm chiều dài `3` đơn vị chiều rộng tăng `4` đơn vị thì hcn thành hvg nên ta có ptr:

       `x-3=39-x+4`

`<=>2x=46`

`<=>x=23` (t/m)

Vậy diện tích hcn ban đầu là: `23.(39-23)=368 m^2`

Nửa chu vi hcn là: $78:2=39\left(m\right)$

Gọi chiều dài hcn ban đầu là: $x\left(m\right)$       $ĐK:3<x<39$

$\Rightarrow$ Chiều rộng hcn ban đầu là: $39-x\left(m\right)$

Vì nếu giảm chiều dài $3$ đơn vị chiều rộng tăng $4$ đơn vị thì hcn thành hvg nên ta có ptr:

       $x-3=39-x+4$

$\iff 2x=46$

$\iff x=23$ (t/m)

Vậy diện tích hcn ban đầu là: $23.(39-23)=368m^2$

`(4x^2-4x+1)-(x+1)^2`

`=(2x-1)^2-(x+1)^2`

`=(2x-1-x-1)(2x-1+x+1)`

`=(x-2).3x`

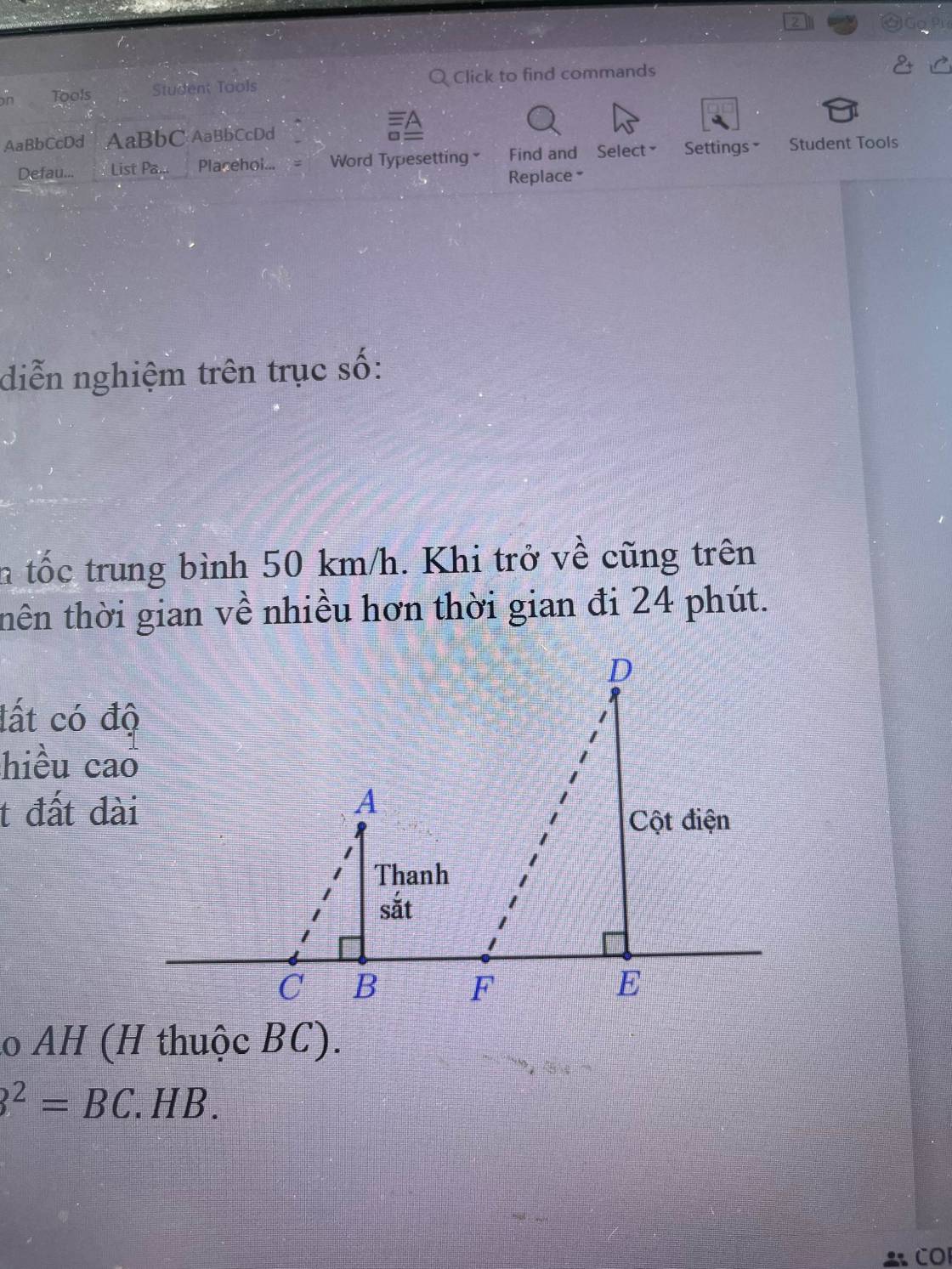
Do các tia sáng được coi là song song nên ta có \(AC//DF\Rightarrow\widehat{ACB}=\widehat{DFE}\) (hai góc đồng vị)

Ta có: \(EF=1,6m;AB=1,8m;BC=0,4m\)

Xét \(\Delta ABC\) và \(\Delta DEF\) có:

\(\widehat{ABC}=\widehat{DEF}=90^0;\widehat{ACB}=\widehat{DFE}\)

\(\Rightarrow\Delta ABC\sim\Delta DEF\) (g.g)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{DE}{EF}\Rightarrow DE=\dfrac{AB.EF}{BC}=\dfrac{1,8.1,6}{0,4}=7,2\left(m\right)\)

Vậy chiều cao cột điện là \(7,2m\).

Vì `AB //// DE=>\hat{ACB}=\hat{DFE}` (`2` góc đồng vị)

Xét `\triangle ABC` và `\triangle DEF` có:

    `{(\hat{ACB}=\hat{DFE}),(\hat{ABC}=\hat{DEF}(=90^o)):}`

  `=>\triangle ABC` $\backsim$ `\triangle DEF` (g-g)

   `=>[AB]/[BC]=[DE]/[EF]`

   `=>[1,8]/[0,4]=[DE]/[1,6]`

   `=>DE=7,2(m)` là chiều cao của cột điện

Hình thang ABCD có hai cạnh bên AD=BC nên nó là hình thang cân

Vậy \(\widehat{D}=\widehat{C}\)

a) Ta có: AB² + AC² = 15² + 20² = 25².

\(\Rightarrow\) BC = 25.

Nên theo định lí Py ta go ( mình trình bày mong bạn thông cảm)

\(\Rightarrow\) Tam giác ABC vuông

b). \(\Delta ACH\approx\Delta BCA\) ( gg ) ( do góc H = góc A = 90; góc C chung ).

\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\Leftrightarrow\dfrac{20}{HC}=\dfrac{25}{20}\Rightarrow HC=\dfrac{20.20}{25}=16\) ( cm ).

c). Ta có: \(MN//AC\)  ( đtb ).

mà \(AC\text{⊥ }AB\)

\(\Rightarrow MN\text{⊥ }AB\)

Xét \(\Delta BIM\) và \(\Delta NBM\) ( gg ).

\(\Rightarrow\dfrac{BM}{IM}=\dfrac{NM}{BM}\Leftrightarrow BM^2=IM.NM\)

A B C D E M

Xét tg cân ABC có

\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{BAC}}{2}=\dfrac{180^o-100^o}{2}=40^o\)

Do BD là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABD}=\widehat{CBD}=\dfrac{40^o}{2}=20^o\)

Trong đoạn BC lấy E sao cho BE=BD

=> tg BID cân tại B => BD=BE (1)

\(\Rightarrow\widehat{BDE}=\widehat{BED}=\dfrac{180^o-\widehat{CBD}}{2}=\dfrac{180^o-20^o}{2}=80^o\)

Xét tg CDE có

\(\widehat{BED}=\widehat{ACB}+\widehat{CDE}\) (trong tg góc ngoài bằng tổng 2 góc trong không kề với nó)

\(\Rightarrow\widehat{CDE}=\widehat{BED}-\widehat{ACB}=80^o-40^o=40^o=\widehat{ACB}\)

=> tg CDE cân tại E => ED=EC (2)

Xét tg ABD có

\(\widehat{ADB}=180^o-\widehat{BAC}-\widehat{ABD}=180^o-100^o-20^o=60^o\)

\(\Rightarrow\widehat{ADE}=\widehat{ADB}+\widehat{BDE}=60^o+80^o=140^o\)

Xét tứ giác ABED có

\(\widehat{ABC}+\widehat{ADE}=40^o+140^o=180^o\) 

=> ABED là tứ giác nội tiếp (Tứ giác có tổng hai góc đối nhau =

180 độ là tứ giác nội tiếp)

\(\Rightarrow\widehat{AED}=\widehat{ABD}\) (góc nội tiếp cùng chắn cung AD)

\(\Rightarrow\widehat{DAE}=\widehat{EBD}\) (góc nội tiếp cùng chắn cung ED)

Mà \(\widehat{ABD}=\widehat{EBD}\)

\(\Rightarrow\widehat{AED}=\widehat{DAE}\) => tg DAE cân tại D => ED=AD (3)

Từ (1) (2) (3) => BD+AD=BE+EC=BC (đpcm)

A B C N I K M D

a/

AM+AN=2AB

Mà

AM=AB-BM

AN=AC+CN

tg ABC cân tại A => AB=AC

=> AB-BM+AB+CN=2AB => BM=CN

b/

Từ N dựng đường thẳng //AB cắt BC kéo dài tại D

Ta có

\(\widehat{ABC}=\widehat{CDN}\) (góc so le trong) (1)

\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân ABC) (2)

\(\widehat{ACB}=\widehat{DCN}\) (góc đối đỉnh) (3)

Từ (1) (2) (3) => \(\widehat{CDN}=\widehat{DCN}\) => tg NCD cân tại N => CN=DN

Mà CN=BM (cmt) 

=> BM=DN mà DN//BM => BMDN là hình bình hành (Tứ giác có cawoj cạnh đối // và = nhau là hbh)

=> IM=IN (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)

Lời giải:
PT $\Leftrightarrow 3-x+3x^2=5-10x$

$\Leftrightarrow 3x^2+9x-2=0$

$\Leftrightarrow 9x^2+27x-6=0$

$\Leftrightarrow (3x+\frac{9}{2})^2=\frac{105}{4}$

$\Rightarrow x=\pm \frac{\sqrt{105}}{6}-\frac{3}{2}$