Tính:\(A=\frac{2x+y}{2x^2-xy}+\frac{16x}{y^2-4x}\)\(+\frac{2x-y}{2x^2+xy}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ gt => ab+bc+ca=0
\(a^2+2bc=a^2+bc+\left(-ab-ac\right)=a\left(a-b\right)-c\left(a-b\right)=\left(a-b\right)\left(a-c\right)\)
Tương tự \(\hept{\begin{cases}b^2+2ac=\left(b-a\right)\left(b-c\right)\\c^2+2ab=\left(c-a\right)\left(c-b\right)\end{cases}}\)
\(A=\frac{1}{\left(a-b\right)\left(a-c\right)}+\frac{1}{\left(b-a\right)\left(b-c\right)}+\frac{1}{\left(c-a\right)\left(c-b\right)}=\frac{b-c+c-a+a-b}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=0\)
Ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Rightarrow ab+bc+ca=0\)
\(\Rightarrow bc=-ab-ca\)
Vậy thì \(a^2+2bc=a^2+bc-ab-ac=a\left(a-b\right)-c\left(a-b\right)=\left(a-c\right)\left(a-b\right)\)
Tương tự ta cũng có:
\(b^2+2ac=\left(b-c\right)\left(b-a\right)\)
\(c^2+2ab=\left(c-a\right)\left(c-b\right)\)
Vậy thì \(A=\frac{1}{a^2+2bc}+\frac{1}{b^2+2ac}+\frac{1}{c^2+2ab}\)
\(A=\frac{1}{\left(a-b\right)\left(a-c\right)}+\frac{1}{\left(b-a\right)\left(b-c\right)}+\frac{1}{\left(c-a\right)\left(c-b\right)}\)
\(A=\frac{-b+c+a-c-a+b}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(A=0.\)

lm tiếp như sau:
\(2x^2-5x\ge3\)
\(\Leftrightarrow2x^2-5x-3\ge0\)
\(\Leftrightarrow2\left(x^2-\frac{5}{2}x-\frac{3}{2}\right)\ge0\)
\(\Leftrightarrow2\left(x^2+\frac{1}{2}x-3x-\frac{3}{2}\right)\ge0\)
\(\Leftrightarrow2\left(x+\frac{1}{2}\right)\left(x-3\right)\ge0\)
Ta có bảng xét dấu
| x | -1/2 3 |
| x+1/2 | - 0 + // + |
| x-3 | - // - 0 + |
| (x+1/2)(x-3) | + 0 - 0 + |
| 2(x+1/2)(x-3) | + 0 - 0 + |
Do đó: \(2\left(x+\frac{1}{2}\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow x\le\frac{1}{2};x\ge3\)
\(x-5\ge\frac{3-x^2}{x}\)
\(\Leftrightarrow\frac{x\left(x-5\right)}{x}\ge\frac{3-x^2}{x}\)
\(\Leftrightarrow x^2-5x\ge3-x^2\)
\(\Leftrightarrow2x^2-5x\ge3\)

\(a,\left(x-3\right)^2-4=0\)
\(\Leftrightarrow\left(x-3\right)^2=4\)
\(\Rightarrow x-3=\pm2\)
\(\hept{\begin{cases}x-3=2\Rightarrow x=5\\x-3=-2\Rightarrow x=1\end{cases}}\)
Vậy \(x=5\)hoặc \(x=1\)
\(b,x^2-2x=24\)
\(\Leftrightarrow x^2-2x+1-1=24\)
\(\Leftrightarrow\left(x-1\right)^2=24+1=25\)
\(\Leftrightarrow x-1=\pm5\)
\(\hept{\begin{cases}x-1=5\Rightarrow x=6\\x-1=-5\Rightarrow x=-4\end{cases}}\)
Vậy \(x=6\) hoặc \(x=-4\)
\(c,\left(2x+1\right)^2+\left(x+3\right)^2-5\left(x-7\right)\left(x+7\right)=0\)
\(\Leftrightarrow4x^2+4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)
\(\Leftrightarrow4x^2+4x+1+x^2+6x+9-5x^2+245=0\)
\(\Leftrightarrow10x+255=0\)
\(\Leftrightarrow10x=-255\)
\(\Leftrightarrow x=\frac{-51}{2}\)
\(d,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\)
\(\Leftrightarrow x^3-27+x\left(2x-x^2+4-2x\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
\(\Leftrightarrow4x-27=1\)
\(\Leftrightarrow4x=28\)
\(\Leftrightarrow x=7\)

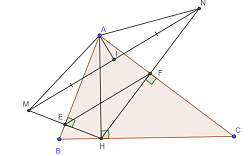
a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.

a) (2x - 5)(3x + b) = ax^2 + x + c
<=> 6x^2 + 2bx -15x -5b = ax^2 + x + c
<=> -ax^2 + 2bx -5b -c = -6x^2 +16x
Đồng nhất hệ số ta có :
+) -a = -6 => a= 6
+) 2b = 16 => b= 8
+) -5b -c= 0 => c= -40
c ) (ax+b)( x^2 -x-1)= ax^3 - cx^2 - 1
<=> ax^3 -ax^2-ax +bx^2-bx-b= ax^3 - cx^2 - 1
<=> (c+b-a)x^2 -(a+b)x -b = -1
Đồng nhất hệ số ta được:
+) c+b-a =0
+) -a-b = 0
+) -b = -1 => b= 1
Thay b=1 ta được a = -1 và c= -2
<p>a) (2x - 5)(3x + b) = ax^2 + x + c<br><=> 6x^2 + 2bx -15x -5b = ax^2 + x + c<br><=> -ax^2 + 2bx -5b -c = -6x^2 +16x<br>Đồng nhất hệ số ta có :<br>+) -a = -6 => a= 6<br>+) 2b = 16 => b= 8<br>+) -5b -c= 0 => c= -40</p>

Giải:
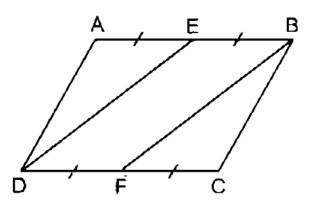
Ta có: AB = CD ( tính chất hình bình hành)
\(EB=\frac{1}{2}AB\left(gt\right)\)
\(FD=\frac{1}{2}CD\left(gt\right)\)
Suy ra: EB = FB (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
A B C D E F
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)


Bài 2:
a) \(VP=\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)\)
\(=a^3+b^3=VT\) (đpcm)
b) \(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
\(=a^3+ab^2+ac^2-a^2b-abc-a^2c+a^2b+b^3+bc^2-ab^2-b^2c-abc\)\(+a^2c+b^2c+c^3-abc-bc^2-ac^2\)
\(=a^3+b^3+c^3-3abc\)
Bài 1:
\(N=\frac{x\left|x-2\right|}{x^2+8x-20}+12x-3\)
\(=\frac{x\left|x-2\right|}{\left(x-2\right)\left(x+10\right)}+12x-3\)
Nếu \(x\ge2\)thì: \(N=\frac{x\left(x-2\right)}{\left(x-2\right)\left(x+10\right)}+12x-3\)
\(=\frac{x}{x+10}+12x+3\) (lm tiếp nhé)
Nếu \(x< 2\) thì: \(N=\frac{x\left(2-x\right)}{\left(x-2\right)\left(x+10\right)}+12x-3\)
\(=\frac{-x}{x+10}+12x-3\) (lm tiếp nhé)
kết quả này có đúng không thì mình chưa chắc bạn nhé : \(\frac{4x+16}{y^2-4x}\)