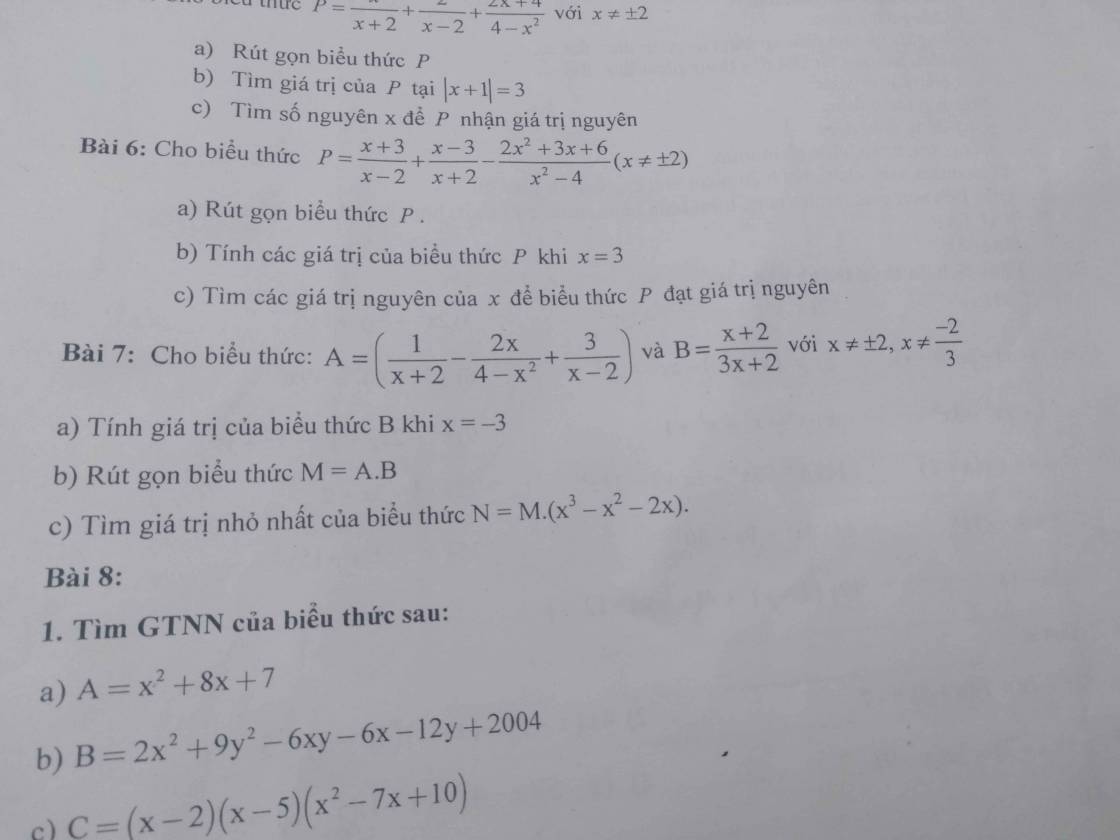 Có ai giúp mình bài 6 câu a với ạ. Mình cảm ơn ạ
Có ai giúp mình bài 6 câu a với ạ. Mình cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`3(x-2)^2+(x-1)^3-x^3=7`
`<=>3x^2-12x+12+x^3-3x^2+3x-1-x^3=7`
`<=>-9x=-4`
`<=>x=4/9`
Vậy `S={4/9}`
\(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=7\)
\(\Leftrightarrow3\left(x^2-4x+4\right)+x^3-3x^2+3x-1-x^3=7\)
\(\Leftrightarrow3x^2-12x+12+\left(x^3-x^3\right)-3x^2+3x-1=7\)
\(\Leftrightarrow\left(3x^2-3x^2\right)+\left(-12x+3x\right)+\left(12-1\right)=7\)
\(\Leftrightarrow-9x+11=7\)
\(\Leftrightarrow9x=4\)
\(\Leftrightarrow x=\dfrac{4}{9}\)

Ta có:
(x+a)(x+b)(x+c) = x^3 + (a+b+c)x^2 +(ab+bc+ca)x + abc
VT = (x^2+ax+bx+ab)(x+c)
= x^3 + ax^2 + bx^2 + abx + cx^2 + cax + bcx + abc (1)
VP = x^3 + (a+b+c)x^2 +(ab+bc+ca)x + abc
= x^3 + ax^2 + bx^2 + abx + cx^2 + cax + bcx + abc (2)
Từ (1) và (2), suy ra:
(x+a)(x+b)(x+c) = x^3 + (a+b+c)x^2 +(ab+bc+ca)x + abc
Mình chỉ làm đc phần a thui, thông cảm nha :)))


H=x2+y2-xy-x+y+1
=>4H=4x2+4y2-4xy -4x +4y +4
4H= (4x2+y2+1-4xy-4x+2y)+3y2+2y +3
4H=(2x-y-1)2+3(y2+\(\dfrac{2}{3}y\) +\(\dfrac{1}{9}\))+ \(\dfrac{8}{3}\)
4H = (2x-y-1)2+3(y+\(\dfrac{1}{3}\) )2 \(+\dfrac{8}{3}\) \(\ge\)\(\dfrac{8}{3}\)(vì \(\left(2x-y-1\right)^2\ge0\forall x,y;3\left(y+\dfrac{1}{3}\right)^2\ge0\forall y\)
=> H \(\ge\dfrac{2}{3}\)
Dấu ''=' xảy ra khi \(\left\{{}\begin{matrix}y=-\dfrac{1}{3}\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy Hmin= 2/3khi x=1/3;y=-1/3
\(H=x^2+y^2-xy-x+y+1\)
\(\Rightarrow4H=4x^2+4y^2-4xy-4x+4y+4\)
\(\Leftrightarrow4A=4x^2+y^2+1-4xy+2y-4x+3y^2+2y+3\)
\(\Rightarrow3.4A=3\left(2x-y-1\right)^2+9y^2+6y+9\)
\(\Leftrightarrow12A=3\left(2x-y-1\right)^2+\left(9y^2+6y+1\right)+8\)
\(\Leftrightarrow12A=3\left(2x-y-1\right)^2+\left(3y+1\right)^2+8\)
Mà \(3\left(2x-y-1\right)^2+\left(3y+1\right)^2+8\ge8\forall x,y\)
\(\Rightarrow12A\ge8\)
\(\Rightarrow A\ge\dfrac{8}{12}=\dfrac{2}{3}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}2x-y-1=0\\3y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=-\dfrac{1}{3}\end{matrix}\right.\)

Như này thì tìm Dmin nhỉ ?
D=x2-xy+x+y2-2y+2015
=>4D=4x2-4xy+4x-8y +8060
4D = (4x2+y2+1-4xy+4x-2y) +3y2-6y +8059
4D = (2x-y+1)2 +3(y2-2y+1) +8056
4D=(2x-y+1)2+3(y-1)2+8056
Vì (2x-y+1)2 \(\ge0\forall xy\) 3(y-1)2 \(\ge0\forall y\)
=> 4D\(\ge\) 8056
=> D\(\ge\) 2014
Dấu ''='' xảy ra khi \(\left\{{}\begin{matrix}\left(2x-y+1\right)^2=0\\3\left(y-1\right)^2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x-y+1=0\\y-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x=y-1\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy Dmin =2014 khi x=0 ;y=1

Gọi x(m) (x>0) là chiều dài mảnh đất hình chữ nhật
Chiều rộng mảnh đất hình chữ nhật là: x-6(m)
Ta có pt : x(x-6)=91
<=>x2-6x-91=0
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=13\\x_2=-7\left(loại\right)\left(x>0\right)\end{matrix}\right.\)
Vậy chiều dài là 13m
Chiều rộng là 13-6=7 (m)
Chu vi vườn hoa là :
2(13+7)=40(m)

\(\left(\sqrt{3}-\sqrt{2}\right)\sqrt{5+2\sqrt{6}}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)\sqrt{3+2+2.\sqrt{3}.\sqrt{2}}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)\left|\sqrt{3}+\sqrt{2}\right|\)
\(=\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)\)
\(=1\)

\(P=\left(\dfrac{2}{x-3}+\dfrac{x^2+3}{9-x^2}+\dfrac{x-1}{x+3}\right):\left(\dfrac{2x-1}{2x+1}-1\right)\)
\(=\left(\dfrac{2}{x-3}-\dfrac{x^2+3}{x^2-9}+\dfrac{x-1}{x+3}\right):\left(\dfrac{2x-1}{2x+1}-\dfrac{2x+1}{2x+1}\right)\)
\(=\dfrac{2\left(x+3\right)-x^2-3+\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}:\dfrac{2x-1-2x-1}{2x+1}\)
\(=\dfrac{2x+6-x^2-3+x^2-4x+3}{\left(x-3\right)\left(x+3\right)}:\dfrac{-2}{2x+1}\)
\(=\dfrac{-2x+6}{\left(x-3\right)\left(x+3\right)}:\dfrac{-2}{2x+1}\)
\(=\dfrac{-2}{\left(x+3\right)}\times\dfrac{2x+1}{-2}\)
\(=\dfrac{2x+1}{x+3}\)


\(P=\dfrac{x+3}{x-2}+\dfrac{x-3}{x+2}-\dfrac{2x^2+3x+6}{x^2-4}\left(x\ne\pm2\right)\)
\(=\dfrac{\left(x+3\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{\left(x-3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x^2+3x+6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+5x+6}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-5x+6}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x^2+3x+6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x^2+5x+6\right)+\left(x^2-5x+6\right)-\left(2x^2+3x+6\right)}{\left(x-2\right)\left(x+2\right)}\)\
\(=\dfrac{x^2+5x+6+x^2-5x+6-2x^2-3x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-3x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=-\dfrac{3}{x+2}\)
Với x khác cộng trừ 2