Giúp me vs ah. Gia đình Hà muốn mua 1 căn nhà ở trung tâm tp Hà Tĩnh để thuận tiện cho việc mua sắm, đi học của con, và khám bệnh khi cần thiết sao cho khoảng cách từ căn nhà đó đến siêu thị, bệnh viện, trường học đều bằng nhau. Hãy giúp Hà xác định vị trí căn nhà cần mua ở đâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.

Gọi A là biến cố "quả bóng lấy ra là số nguyên tố"
=>A={5}
=>n(A)=1
\(P\left(A\right)=\dfrac{1}{5}\)
Gọi B là biến cố "Quả bóng lấy ra ghi số chia hết cho 5"
=>B={5;10;15;20;25}
=>n(B)=5
\(P\left(B\right)=\dfrac{5}{5}=1\)
Gọi C là biến cố "Quả bóng lấy ra ghi số chia hết cho 6"
=>C=\(\varnothing\)
=>\(P\left(C\right)=0\)
a: Biến cố chắc chắn là biến cố B
b: \(P\left(A\right)=\dfrac{1}{5}\)
a, Biến cố "quả bóng lấy ra ghi số nguyên tố" là biến cố ngẫu nhiên
Biến cố " quả bóng lấy ra ghi số chia hết cho 5" là biến cố chắc chắn
Biến cố " quả bóng lấy ra ghi số chia hết cho 6" là biến cố không thể
b, Xác suất của biến cố"quả bóng lấy ra ghi số nguyên tố"là 1/5

Hình bạn tự vẽ nhé
a,Xét tam giác BAD và tam giác EDA:
AD chung
ABD=AED=90 độ( tam giác ABC vuông tại B, DE vuông góc AC)
BAD=CAD(AD là tia phân giác)
Suy ra tam giác BAD= tam giác EDA(cạnh huyền - góc nhọn)
b, Vì tam giác BAD= tam giác EDA (cmt)
Suy ra: AB=AE(2 cạnh tương ứng)
Suy ra A thuộc trung trực BE 1
Vì tam giác BAD = tam giác EDA(CMA)
Suy ra:BD=DE
Suy ra: D thuộc trung trực BE 2
Từ 1 và 2
Suy ra AD là đường trung trực BE
c,AB=AE(cmt) 3
BK=EC(gt) 4
AB+BK=AK 5
AE+EC=AC 6
Từ 3,4,5,6
Suya ra AK =AC
Suy ra tam giác AKC cân tại A 7
Mà AD là tia phân giác 8
Từ 7 và 8
Suy ra AD là đg cao tam giác AKC
Xét tam giác AKC có:
Đg cao CB( tam giác ABC vuông tại B)
Đg cao AD (cmt)
Mà AD cắt CB tại D
Suy ra D là trực tâm tam giác AKC 9
Suy ra KE là đg cao còn lại 10
Từ 9,10
Suy ra D thuộc KE
Suy ra K,D,E thg hàng

a, P(x) = 6x^3 - 3x^2 + 5x - 1
Q(x) = -6x^3 + 3x^2 - 2x + 7
b, P(x) + Q(x)
= ( 6x^3 - 3x^2 + 5x - 1 ) + ( -6x^3 +3x^2 - 2x +7 )
= 6x^3 - 3x^2 + 5x -1 + ( -6x^3 ) + 3x^2 - 2x +7
= [ 6x^3 + ( -6x^3) ] + (-3x^2 + 3x^2 ) + ( 5x - 2x ) + ( -1 +7 )
= 3x + 6
P(x) - Q(x)
= (6x^3 - 3x^2 + 5x - 1 ) - (-6x^3 + 3x^2 - 2x + 7 )
= 6x^3 - 3x^2 + 5x -1 - 6x^3 - 3x^2 + 2x - 7
= ( 6x^3 - 6x^3 ) + (-3x^2 - 3x^2 ) + ( 5x +2x ) + ( -1 - 7 )
= -6x^2 + 7x + ( -8)

Lời giải:
\(A=(\frac{-3}{4}x^2y^5).(4x^3y)=\frac{-3}{4}.4(x^2.x^3)(y^5.y)\\
=-3x^5y^6\)
Hệ số: $-3$
Phần biến: $x^5y^6$
Bậc: $5+6=11$
c.
Tại $x=-1$ và $y=1$ thì:
$A=-3(-1)^5.1^6=3$

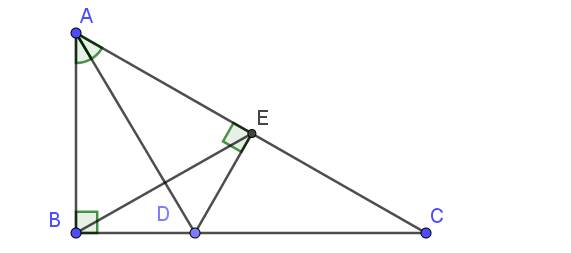
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó; ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực củaAD(2)
Từ (1),(2) suy ra BE là đường trung trực của AD
b: Xét ΔBAD có
AH,BE là các đường cao
AH cắt BE tại I
Do đó: I là trực tâm của ΔBAD
=>DI\(\perp\)AB
mà AC\(\perp\)AB
nên DI//AC
c: Gọi K là giao điểm của CF và BA
Xét ΔBKC có
BF,CA là các đường cao
BF cắt CA tại E
Do đó: E là trực tâm của ΔBKC
=>KE\(\perp\)BC
mà ED\(\perp\)BC
và KE,ED có điểm chung là E
nên K,E,D thẳng hàng
=>BA,ED,CF đồng quy
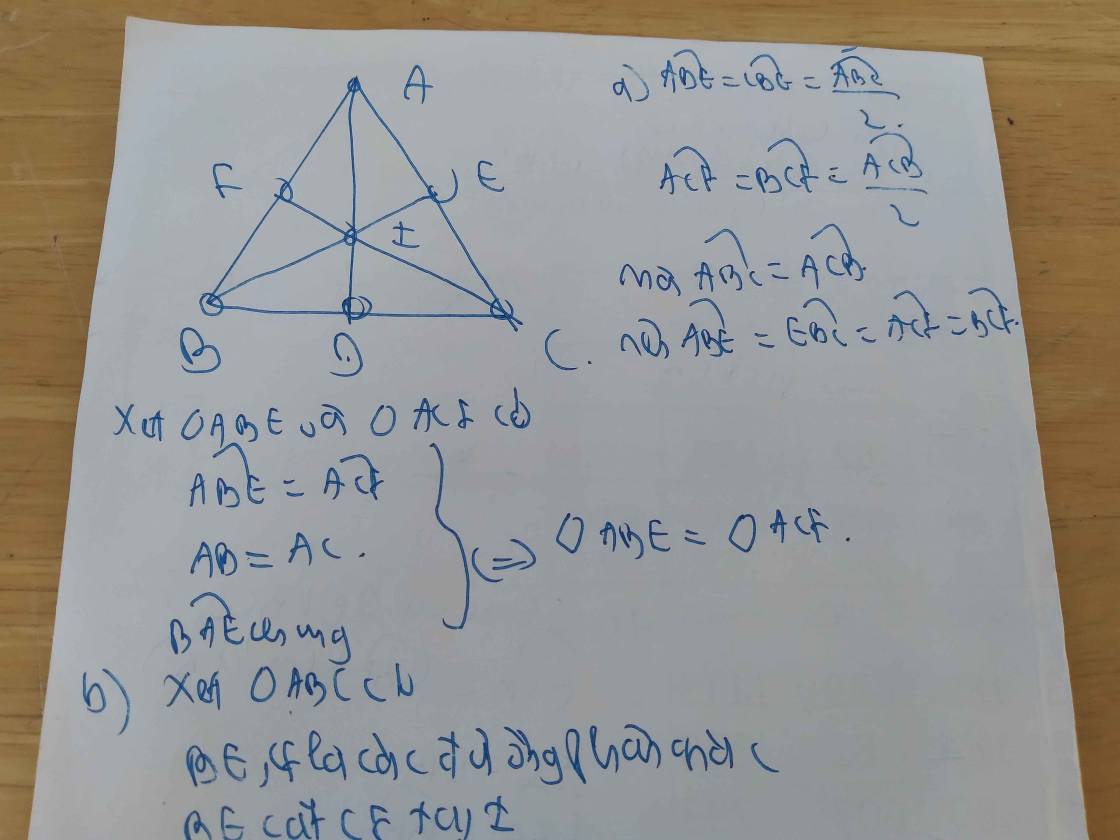


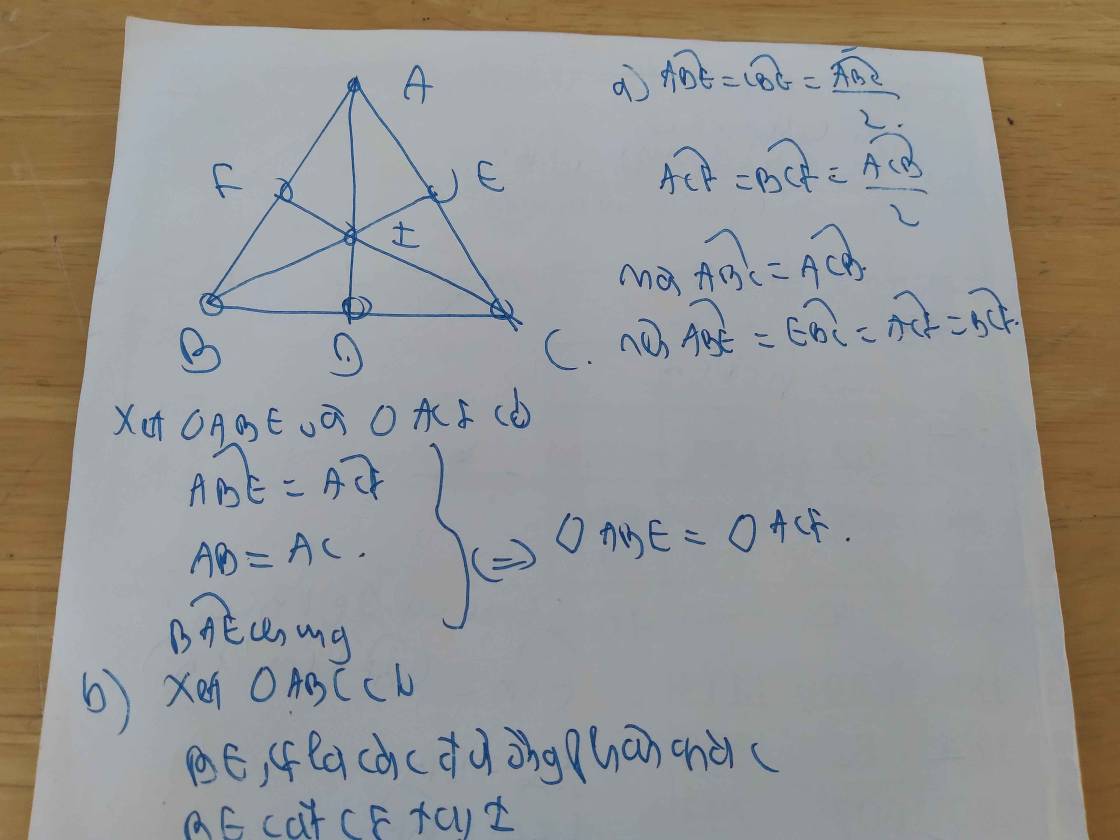








Để khoảng cách từ vị trí của nhà Hà đến siêu thị, bệnh viện, trường học đều bằng nhau thì nhà Hà nằm ở vị trí D là giao điểm của ba đường trung trực của ∆ABC như hình vẽ.
Siêu thị, bệnh viện, trường học nằm ở ba vị trí là ba đỉnh của ∆ABC