Tìm x y z biết 3x=4y=5z và x+2y-3z=28
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{4}{3}-\left(\dfrac{5}{3}-\dfrac{3}{4}+\dfrac{5}{18}\right)+\left(\dfrac{9}{4}-\dfrac{8}{3}\right)\\ A=\dfrac{4}{3}-\dfrac{5}{3}+\dfrac{3}{4}-\dfrac{5}{18}+\dfrac{9}{4}-\dfrac{8}{3}\\ A=\left(\dfrac{4}{3}-\dfrac{5}{3}-\dfrac{8}{3}\right)+\left(\dfrac{3}{4}+\dfrac{9}{4}\right)-\dfrac{5}{18}\\ A=-3+3-\dfrac{5}{18}\\ A=-\dfrac{5}{18.}\)


Lời giải:
Ta thấy:
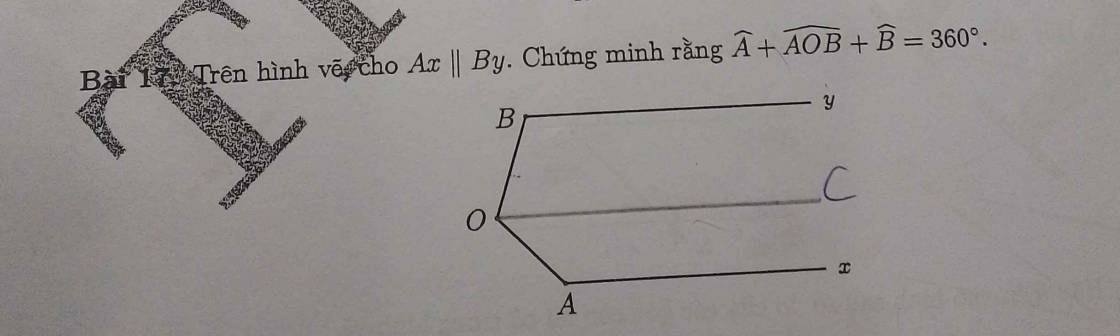
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)

\(\dfrac{-4}{7}:x=\dfrac{-2}{5}\)
\(\Rightarrow x=\dfrac{-4}{7}:\dfrac{-2}{5}\)
\(\Rightarrow x=\dfrac{10}{7}\)
\(\dfrac{-4}{7}:x=\dfrac{-2}{5}\)
\(x=\dfrac{-4}{7}.\dfrac{-5}{2}\)
\(x=\dfrac{10}{7}\)

\(\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}{\dfrac{19}{1}+\dfrac{18}{2}+\dfrac{17}{3}+....+\dfrac{1}{19}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}{1+\left(\dfrac{18}{2}+1\right)+\left(\dfrac{17}{3}+1\right)+\left(\dfrac{1}{19}+1\right)}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}}{1+\dfrac{20}{2}+\dfrac{20}{3}+...+\dfrac{20}{19}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}}{20.\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{19}+\dfrac{1}{20}\right)}\)
\(=\dfrac{1}{20}\)



\(\dfrac{-4}{13}.\dfrac{5}{17}+\dfrac{-12}{13}.\dfrac{4}{17}\)
= \(\dfrac{-4}{13}.\dfrac{5}{17}+\dfrac{-4}{13}.\dfrac{12}{17}\)
= \(\dfrac{-4}{13}.\left(\dfrac{5}{17}+\dfrac{12}{17}\right)\)
= \(\dfrac{-4}{13}.\dfrac{17}{17}\)
= \(\dfrac{-4}{13}.1\)
= \(\dfrac{-4}{13}\)
= \(\dfrac{-4.5-12.4}{13.17}\)
=\(\dfrac{-4\left(5+12\right)}{13.17}\)
=\(\dfrac{-4.17}{13.17}\)
=\(\dfrac{-4}{13}\)

(x + 1)4 = (x + 1)3
⇒ (x + 1)4 - (x + 1)3 = 0
⇒ (x + 1)3 . (x + 1 - 1) = 0
⇒ (x + 1)3 . x = 0
⇒ \(\left[{}\begin{matrix}\left(x+1\right)^3=0\\x=0\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=-1\\x=0\end{matrix}\right.\)
Vậy \(x\in\left\{0;-1\right\}\)

Ta có :
\(3x=4y=5z\)
\(\Rightarrow\dfrac{x}{\dfrac{1}{3}}=\dfrac{2y}{\dfrac{1}{2}}=\dfrac{3z}{\dfrac{3}{5}}=\dfrac{x+2y-3z}{\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{3}{5}}=\dfrac{28}{\dfrac{7}{30}}=\dfrac{28.30}{7}=120\) \(\left(x+2y-3z=28\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}.120=40\\y=\dfrac{1}{4}.120=30\\z=\dfrac{1}{5}.120=24\end{matrix}\right.\)